- Espace Euclidien
-
Espace euclidien
En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le plan ainsi que l'espace qui nous entoure. Un espace euclidien permet également de traiter les dimensions supérieures ; il est défini par la donnée d'un espace vectoriel sur les nombres réels, de dimension finie, muni d'un produit scalaire, qui permet de mesurer distances et angles.
L'existence d'un produit scalaire permet d'obtenir par exemple des bases particulières dites orthonormales, une relation canonique entre l'espace et son dual, ou des familles d'endomorphismes admettant une théorie simple de réduction. Il permet aussi d'obtenir une structure topologique, ce qui met à disposition les méthodes d'analyse.
Les espaces euclidiens possèdent une longue histoire ainsi que de nombreuses applications. Les relations entre cet outil et le reste des mathématiques sont multiples et variées, depuis la logique et l'algèbre jusqu'aux géométriques non euclidiennes. Cet aspect est traité dans l'article géométrie euclidienne.
Sommaire
Espace euclidien et bipoints
Articles détaillés : Vecteur et Produit scalaire.Dans le cadre de la construction des vecteurs à l'aide de classe d'équivalence de bipoints sur un espace affine, une première définition du produit scalaire peut être obtenue. La norme d'un vecteur correspond à la longueur d'un bipoint représentatif, l'angle de deux vecteurs correspond à celui de deux bipoints représentatifs de même origine. La formule donnant le produit scalaire est alors :
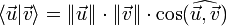
Dans de nombreux cas en physique classique ou en géométrie analytique, si la dimension de l'espace n'est pas trop élevée (typiquement deux ou trois), cette définition est suffisante. Toutefois, dans le cas général, ce formalisme s'avère à la fois lourd et peu adapté pour, par exemple, l'étude des propriétés topologiques d'un espace euclidien. Une deuxième approche, purement algébrique et plus abstraite, existe, et permet d'établir plus facilement des résultats plus généraux[1].
Formalisation et premières propriétés
Définitions
Les axiomes d'un espace vectoriel euclidien E concernent deux structures qui se combinent : la première est celle d'espace vectoriel de dimension finie sur le corps des nombres réels, et la deuxième est la donnée d'une forme bilinéaire, notée ici <. , .>, appelée produit scalaire, possédant des propriétés spécifiques. Une forme bilinéaire est une application de E2 (l'ensemble des couples d'éléments de E) dans l'ensemble R des réels, linéaire pour chacune des deux variables, et il s'agit d'un produit scalaire si elle possède de plus les trois propriétés :
-
- Un produit scalaire est symétrique, ce qui signifie :

-
- Un produit scalaire est positif ce qui signifie :
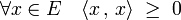
-
- Un produit scalaire est défini positif ce qui signifie qu'il est positif et que de plus :
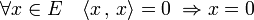
Définition[2] — Un produit scalaire sur un espace vectoriel réel E est une forme bilinéaire symétrique définie positive.
En particulier, la définition de produit scalaire est valable en dehors du cadre de la dimension finie. Elle se généralise aux espaces complexes, (cf l'article Hermitien).
Définition — Un espace vectoriel euclidien est un espace vectoriel réel de dimension finie muni d'un produit scalaire.
Définition — Un espace affine euclidien est un espace affine dont l'espace vectoriel sous-jacent est muni d'une structure euclidienne.
La donnée du produit scalaire permet de définir une norme et une distance :
Définition — La norme euclidienne associée à un espace vectoriel du même type est la fonction de E dans l'ensemble des réels positifs, qui à un vecteur x associe la racine carrée du produit scalaire de x avec lui-même. La norme euclidienne du vecteur x est souvent notée
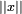 . Cette convention est utilisée tout au long de l'article.
. Cette convention est utilisée tout au long de l'article.Cette fonction vérifie les axiomes de la notion de norme.
Définition — La distance euclidienne est la distance associée à la norme euclidienne. La distance euclidienne de deux vecteurs x et y est la norme de la différence x - y.
Cette fonction vérifie les axiomes de la notion de distance. Dans le cas d'un espace affine, la distance entre deux point a et b est égale à la norme du vecteur d'extrémités a et b.
Exemples
- L'espace vectoriel Rn, muni du produit scalaire canonique
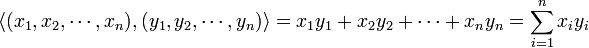
- est un espace euclidien appelé espace euclidien canonique[3] de dimension n.
- L'espace vectoriel des polynômes réels de degré inférieur ou égal à n,
-
- muni du produit scalaire canonique :
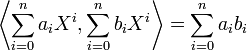
- est un espace euclidien de dimension n + 1.
-
- muni du produit scalaire :

- est aussi un espace euclidien dont la norme et la distance associées sont différentes de la précédente. Ce produit scalaire est plus généralement défini sur l'espace des polynômes réels, sans condition de degré (espace de dimension infinie).
-
- muni du produit scalaire :
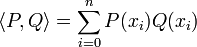
- (où x0, ... xn sont n + 1 réels distincts) est aussi un espace euclidien dont la norme et la distance associées sont différentes des précédentes.
- L'espace des nombres complexes C est un espace vectoriel réel de dimension deux. L'application qui à deux complexes x et y associe la partie réelle du produit de x et du conjugué de y est un produit scalaire, conférant à C une structure d'espace vectoriel euclidien.
- De manière plus générale, un espace hermitien de dimension n est euclidien s'il est considéré comme un espace réel de dimension 2.n avec comme produit scalaire la partie réelle du produit scalaire d'origine.
Inégalités de Cauchy-Schwarz et de Minkowski
Articles détaillés : Inégalité de Cauchy-Schwarz et Inégalité de Minkowski.Deux majorations sont largement utilisées dans l'étude des espaces euclidiens. Celle de Cauchy-Schwarz établit une relation entre un produit scalaire et deux normes :
Inégalité de Cauchy-Schwarz — La valeur absolue du produit scalaire de deux vecteurs x et y est majorée par le produit des normes de x et de y.
Cette majoration s'écrit :
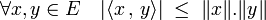
L'égalité n'a lieu que si x et y sont colinéaires. La démonstration de ce résultat est donnée dans l'article associé.
Inégalité de Minkowski — La norme de la somme de deux vecteurs x et y est inférieure ou égale à la somme des normes de chacun des vecteurs.
Cette majoration s'écrit :
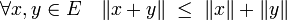
L'égalité n'a lieu que si x et y sont colinéaires et de même sens. Cette majoration correspond au troisième axiome définissant une norme, dit de sous-additivité ou inégalité triangulaire. Elle est démontrée dans l'article associé.
Propriétés algébriques
Base orthonormale
Articles détaillés : Base orthonormale et Procédé de Gram-Schmidt.Dans l'étude des espaces euclidiens, certaines bases de l'espace vectoriel sous-jacent sont d'un intérêt particulier. Ce sont celles qui vérifient les propriétés suivantes, en liaison avec la structure supplémentaire amenée par le produit scalaire : chaque vecteur de la base possède une norme égale à un et deux vecteurs distincts de la base sont orthogonaux, c'est-à-dire que leur produit scalaire est égal à zéro. Une telle base est qualifiée d'orthonormale.
Orthogonalité et vecteurs libres 1 — Toute famille de vecteurs non nuls et orthogonaux deux à deux est une famille libre.
L'existence de bases orthonormale est assurée par la proposition suivante, utile dans de nombreuses situations :
Orthogonalité et vecteurs libres 2 — Soit x et y deux vecteurs libres, alors le vecteur z égal à y - <x , y>/<x , x> x est non nul et orthogonal à x.
En effet, si x et y forment une famille libre alors x est non nul, et la combinaison linéaire définissant z ne l'est pas non plus. Le calcul suivant montre que la famille (x, z) est orthogonale.
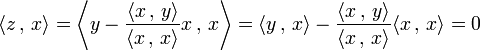
Le procédé de Gram-Schmidt, qui généralise ce calcul dans le cas de familles libres comptant plus de deux vecteurs, montre l'existence de base orthonormale, et une méthode pour en calculer explicitement, à partir de la donnée d'une base préalable :
Existence d'une base orthonormale — Tout espace euclidien possède une base orthonormale.
Dans une base orthonormale la norme et le produit scalaire s'expriment facilement en fonction des coordonnées. Soit (e1, ..., en) une base orthonormale notée B, x et y deux vecteurs quelconques de E de coordonnées (x1, ..., xn) et (y1, ..., yn) dans la base B. Les expressions suivantes fournissent la norme et le produit scalaire :

En particulier, tout espace vectoriel euclidien de dimension n est isomorphe à Rn, c'est-à-dire qu'il existe une application linéaire bijective de E dans Rn, respectant les deux produits scalaires.
Orthogonalité et convexité
Articles détaillés : Théorème de projection sur un convexe fermé, Projection orthogonale et Orthogonalité.Dans ce paragraphe, x désigne un vecteur et C un convexe fermé de E. La distance entre x et C désigne le minimum des distances entre x et un point de C.
Théorème de projection sur un convexe fermé — Il existe une unique application t de E dans C, dite projection sur le convexe, qui à x associe le point t(x) de C, tel que la distance de x à C soit égale à celle de x à t(x). Le vecteur t(x) est l'unique point de C vérifiant les deux propositions suivantes, qui sont équivalentes :
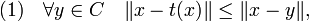
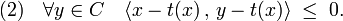
La projection est idempotente, c'est-à-dire que la composée de t avec elle-même est égale à t ; elle est contractante, c'est-à-dire que les images de deux points sont à une distance moindre que leurs antécédents ; enfin elle est monotone au sens où si x1 et x2 sont deux vecteurs de E, alors <t(x1) - t(x2) , x1 - x2 > est positif. Les démonstrations sont données dans l'article associé.
En particulier, ce résultat s'applique pour un sous-espace vectoriel F (le caractère fermé d'un sous-espace vectoriel, en dimension finie, est démontré en deuxième partie de l'article). Le théorème de meilleure approximation affirme l'existence d'une application p qui à x associe un élément p(x) de F tel que la distance entre x et F est égale à celle entre x et p(x).
Définition et propriétés — L'application p est linéaire idempotente, son image et son noyau sont deux sous-espaces vectoriels orthogonaux et supplémentaires. Si x est un vecteur de E alors p(x) est l'unique vecteur de F tel que x - p(x) est orthogonal à F. Une telle application p est appelée projecteur orthogonal.
Les propriétés associées à l'orthogonalité et aux projecteurs sont développées dans les articles associés.
Dans le cas où F est le sous-espace vectoriel engendré par une famille B orthonormale (fi), ce résultat s'interprète en coordonnées, pour donner l'inégalité de Bessel :
Définitions et inégalité de Bessel — Soit x un élément de E, p(x) est le vecteur de coordonnées (<x , fi>) dans la base (fi) et la somme des carrés de ses coordonnées est un nombre réel inférieur au carré de la norme de x. Les différentes coordonnées sont appelées coefficients de Fourier. Dans le cas où F est égal à E, ils correspondent aux coordonnées de x dans la base B, qui est alors une base de E.
Cette technique possède des applications, par exemple, en statistique, et elle est le fondement de la méthode des moindres carrés.
Démonstrations-
- p(x) est l'unique vecteur de F tel que p(x) est orthogonal à x - p(x) :
Soit y un élément quelconque de F, y + p(x) ainsi que y - p(x) sont deux éléments de F. La propriété (2) du théorème de meilleure approximation montre que <x - p(x) , y>, ainsi que - <x - p(x), y> sont tous deux inférieurs ou égaux à zéro. Ce qui montre que x - p(x) est orthogonal à F.
De plus <x - y , p(x) - y> est égal à <x - p(x) + p(x) - y , p(x) - y> ou encore au carré de la norme de p(x) - y. Donc, si x - y est orthogonal à F alors y est égal à p(x), ce qui montre l'unicité du vecteur.
-
- L'application p est linéaire :
Soit x1, x2 deux vecteurs de E et λ un nombre réel. p(x1 + λx2) est l'unique vecteur de F tel que x1 + λx2 - p(x1 + λx2) soit élément de l'orthogonal de F. Cette propriété est manifestement vérifiée par le vecteur x1 - p(x1) + λ(x2 - p(x2)). Ce qui montre que p(x1 + λx2) est égal à p(x1) + λ(x2) et la linéarité de p.
-
- L'application p est un idempotente d'image F et de noyau son orthogonal.
Tout projecteur de meilleure approximation est idempotent, c'est donc le cas pour p, qui est donc un projecteur. Sur F l'application p est manifestement égal à l'identité il est donc inclus dans l'image. La première proposition démontrée prouve que l'orthogonal de F est incluse dans le noyau. Comme F et son orthogonal sont supplémentaires, F est l'image de p et son noyau est son orthogonal.
-
- Inégalité de Bessel :
Soit (αi ) les coefficients de p(x) dans la base B de F. Le vecteur x - p(x) est orthogonal à fi, ce qui montre que :

Ce qui démontre l'inégalité de Bessel car
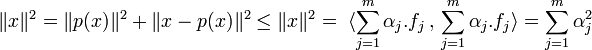
Dans le cas où F est égal à E, l'égalité devient :
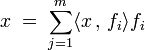
Espace dual et forme bilinéaire
Articles détaillés : Espace dual et Forme bilinéaire.Le dual E* de E désigne l'espace des formes linéaires sur E. Le produit scalaire fournit une application canonique φ de E dans E*, qui à tout vecteur x de E associe la forme linéaire x* définie par :
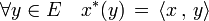
L'application φ est linéaire. Si x est un élément du noyau de l'application φ, alors, en particulier, x*(x) est égal à zéro donc la norme de x est nulle ; ainsi, φ est injective. De l'égalité des dimensions de E et de E* il résulte que l'application φ est aussi surjective. Ceci montre la propriété suivante :
Proposition 1 — Il existe un isomorphisme canonique entre un espace euclidien et son dual.
L'isomorphisme φ est très largement utilisé, en mathématiques comme en physique. Par exemple un champ scalaire, c'est-à-dire une application différentiable de E dans R, possède comme différentielle une application de E dans l'ensemble des formes linéaires sur E. L'identification du dual et de E à l'aide de l'isomorphisme φ permet de représenter les formes linéaires sur E par des éléments de E. La différentielle prend alors le nom de gradient. En physique, la force est un élément du dual des vecteurs de l'espace géométrique. Elle est identifiée à un vecteur de l'espace, même si elle n'est pas de même nature. Cette technique permet une représentation plus intuitive ainsi qu'un calcul simple. Le travail de la force, une grandeur importante en physique, s'interprète comme le produit scalaire avec la force.
Il est possible de construire de manière analogue deux morphismes ψ1 et ψ2 entre L(E) l'ensemble des endomorphismes de E dans L2(E) l'espace des formes bilinéaires. À un endomorphisme a, on associe ψ1a et ψ2a définis par :
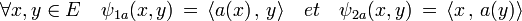
Un raisonnement analogue au précédent montre que ψ1 et ψ2 sont deux applications linéaires injectives. La surjectivité est la conséquence du fait que L(E) et L2(E) ont même dimension, à savoir n2.
Proposition 2 — Les applications ψ1 et ψ2 sont deux isomorphismes canoniques entre l'ensemble des endomorphismes et des formes bilinéaires sur un espace euclidien.
Adjoint d'un endomorphisme
Article détaillé : adjoint d'un endomorphisme.Les isomorphismes précédents possèdent d'autres applications. La composée de ψ1 et de l'inverse de ψ2 est une application de L(E) dans lui-même. Comme ψ1 et ψ2 sont deux isomorphismes, la composée est encore un isomorphisme. Cette application associe à l'endomorphisme a, l'application, en général notée a* définie par :
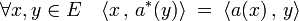
Définition et propriétés — L'application de L(E) dans lui-même, qui à a associe l'endomorphisme a* est un isomorphisme involutif. L'image de a par cette application est appelée adjoint de a. Cet isomorphisme est diagonalisable et admet deux valeurs propres 1 et -1. Les vecteurs propres de valeurs propres 1 (resp. -1) sont appelés autoadjoints (resp. antisymétriques).
Il existe une famille importante d'endomorphismes, comprenant notamment les endomorphismes autoadjoints et les endomorphismes antisymétriques : ceux qui commutent avec leur adjoint. Une application linéaire ayant cette propriété est dite normale. Un cas particulier important est celui des automorphismes orthogonaux, c'est-à-dire les automorphismes u qui laissent invariant le produit scalaire :
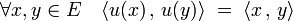
L'ensemble des automorphismes vérifiant cette propriété forme un groupe appelé groupe orthogonal.
La relation induite par le produit scalaire entre les formes bilinéaires et les endomorphismes possède de nombreuses applications, dans des domaines très divers (voir notamment l'article théorème spectral dans le cas où les formes sont symétriques et les endomorphismes autoadjoints).
Construction d'espaces euclidiens
Comme fréquemment en algèbre, la donnée d'espaces euclidiens permet d'en construire de nouveaux.
Sous-espace, espace produit
Si F est un sous-espace vectoriel d'un espace euclidien, alors la restriction du produit scalaire induit une structure d'espace vectoriel euclidien sur F.
Si E1 et E2 sont deux espaces euclidiens, alors leur produit dispose d'une structure euclidienne. Le produit scalaire est donné par la formule :
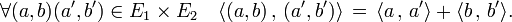
Espace quotient
La nature des projecteurs orthogonaux permet d'attribuer un produit scalaire à un quotient d'un espace euclidien. La norme d'une classe de x de l'ensemble E/F correspond à la distance entre un représentant de la classe et F. Si
 représente la classe de x, alors le produit scalaire <. , . >E/F sur E/F est défini par :
représente la classe de x, alors le produit scalaire <. , . >E/F sur E/F est défini par :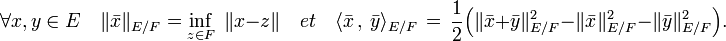
Il existe une isométrie canonique entre le supplémentaire orthogonal de F (muni de la structure d'espace euclidien en tant que sous-espace vectoriel), et le quotient E/F, muni de la structure d'espace euclidien décrite précédemment, qui à tout élément de ce supplémentaire orthogonal associe sa classe dans E/F. Ceci provient de l'identité, suivante, où p est le projecteur orthogonal de direction F :
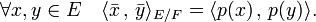
Produit tensoriel
Soient E1 et E2 deux espaces euclidiens de dimensions respectives n1 et n2, s'ils sont identifiés à leurs duaux à l'aide de l'isomorphisme canonique φ, l' espace tensoriel E1
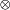 E2 s'identifie à l'ensemble des formes bilinéaires de E1xE2. Le produit tensoriel est une application bilinéaire de E1xE2 dans E1
E2 s'identifie à l'ensemble des formes bilinéaires de E1xE2. Le produit tensoriel est une application bilinéaire de E1xE2 dans E1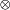 E2 définie par :
E2 définie par :
L'image de E1xE2 par le produit tensoriel est une partie génératrice de E1
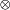 E2, il suffit donc de définir le produit scalaire sur cette image pour le définir sur tout l'espace. Le produit scalaire est alors défini par l'égalité suivante :
E2, il suffit donc de définir le produit scalaire sur cette image pour le définir sur tout l'espace. Le produit scalaire est alors défini par l'égalité suivante :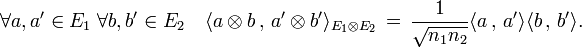
Endomorphisme
Si E1 et E2 sont confondus, le produit scalaire précédent est celui de L2(E). L'isomorphisme canonique ψ1 de L(E) dans L2(E) permet de munir L(E) d'une structure d'espace euclidien :
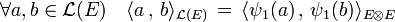
Le choix de l'isomorphisme ψ1 ou ψ2, définis dans le paragraphe Espace dual et forme bilinéaire, est arbitraire, ils amènent tous deux au même produit scalaire. Ce produit scalaire de L(E) confère aux deux isomorphismes le caractère d'isométrie.
L'adjoint permet une expression plus simple du produit scalaire sur L(E). le produit scalaire de deux endomorphismes a et b correspond à la trace de l'endomorphisme adjoint de b composée avec a :
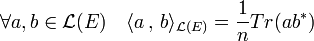
Pour ce produit scalaire, les endomorphismes autoadjoints et antisymétriques forment deux sous-espaces orthogonaux en somme directe et le groupe orthogonal est inclus dans la sphère unité.
Géométrie
Géométrie du triangle
Article détaillé : Triangle. Le cercle d'Euler est un exemple de propriétés démontrables dans le cadre d'un espace euclidien.
Le cercle d'Euler est un exemple de propriétés démontrables dans le cadre d'un espace euclidien.
Un espace euclidien dispose naturellement d'une distance. Il est possible de définir un angle entre deux vecteurs x et y non nuls. Un angle apparaît comme une classe d'équivalence entre des couples de vecteurs non nuls. Soit (a, b) un couple de vecteurs non nuls représentant un angle Θ ; l'angle entre x et y est égal à Θ si et seulement s'il existe une rotation dont l'image de a (resp. b) est égale à x (resp. y).
Si E est de dimension deux, alors il est possible d'orienter l'espace et l'angle (x, y) n'est pas nécessairement égal à celui de (y, x). Pour les autres dimensions, il existe toujours une rotation dont l'image de x (resp. y) est égale à y (resp. y) et un angle orienté ne fait pas sens.
La mesure θ d'un angle Θ est donnée par la formule suivante, si (x, y) est un représentant de l'angle :
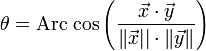
Cette définition permet de formaliser un espace disposant de la même géométrie du triangle, que celle fondée sur les célèbres postulats décrits dans le livre d'Euclide, les Éléments. Une telle géométrie vérifie les théorèmes de Thalès, de Pythagore, ou d'Al-Kashi.
Un exemple classique est donné par le cercle d'Euler disposant de neuf points remarquables.
Caractérisation par la forme polaire
Le produit scalaire confère la dimension euclidienne à un espace vectoriel de dimension finie. La question se pose de savoir s'il n'existe pas d'autres moyens pour caractériser un espace euclidien. Une analyse montre qu'une norme est un outil suffisant.
Proposition 1 — Soit N une norme de E. N est euclidienne si et seulement si l'application φ de ExE dans R, qui à deux vecteurs x et y associe la valeur suivante, dite identité de polarisation est un produit scalaire. Il correspond alors au produit scalaire conférant à E le statut d'espace euclidien de norme N.
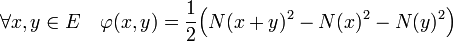
On remarque que si l'application φ est bilinéaire, alors N2 est une forme quadratique. L'égalité précédente montre que la connaissance d'une forme bilinéaire sur la diagonale de ExE suffit à déterminer intégralement φ. Ceci donne lieu à la définition suivante :
Définition — La forme bilinéaire φ est appelée forme polaire de la forme quadratique N2.
Il existe une autre manière de définir le produit scalaire, à partir de l'égalité dite règle du parallélogramme. Cette égalité stipule que la somme des carrés des longueurs des deux diagonales d'un parallélogramme est égale au double de la somme des carrés de deux cotés adjacents. Elle prend la forme suivante :
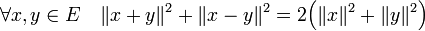
Une légère modification de la formule permet d'établir le résultat suivant :
Proposition 2 — Soit N une norme de E. N est euclidienne si et seulement si l'application φ de ExE dans R, qui à deux vecteurs x et y associe la valeur suivante, encore appelée identité de polarisation est un produit scalaire. Il correspond alors au produit scalaire conférant à E le statut d'espace euclidien de norme N.

La modification de la formule n'est néanmoins pas nécessaire, le résultat suivant est aussi vérifié :
Proposition 3 — Toute norme N de E vérifiant l'égalité du parallélogramme confère à E le statut d'espace euclidien.
La dernière proposition est démontrée dans l'article Identité de polarisation.
Caractérisation par une surface quadrique
Article détaillé : Quadrique. La donnée d'un ellipsoïde caractérise un produit scalaire et donc un espace euclidien.
La donnée d'un ellipsoïde caractérise un produit scalaire et donc un espace euclidien.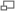
Ici, A désigne un espace affine d'espace vectoriel sous-jacent E de dimension finie n sur R. L'objectif est ici de munir E d'un produit scalaire à l'aide d'une surface quadrique particulière. L'espace A est muni d'un repère cartésien Rep. Une surface quadrique désigne ici l'ensemble des points vérifiant une équation du second degré. Si (xi) désigne les coordonnées du point X de A dans Rep, il existe alors un polynôme Q[X] à n variables et de degré deux tel que les points de la surface quadrique S sont définies par :
![\forall X \in S \quad Q[x_1,\cdots , x_n] = 0](/pictures/frwiki/51/35f2caa760d9979b3f23c8eadebda7ec.png)
Il existe plusieurs géométries possibles pour une quadrique. Un cas particulier correspond à celui où la surface S est compact. En dimension trois, la quadrique est qualifiée d'ellipsoïde. La lettre O désigne ici le centre de la quadrique. La donnée de ce point établit une isométrie entre A et E, à chaque point a de A est associé le vecteur d'origine O et d'extrémité a. Le théorème suivant assure que la donnée d'une telle surface est équivalente à celle d'un produit scalaire sur E.
Caractérisation par une quadrique — Si E est euclidien, la sphère unité est une quadrique compacte non réduite à un point dans tout repère cartésien de A. Réciproquement si S est une surface quadrique compacte non réduite à un point, alors S correspond à la sphère unité pour un unique produit scalaire de E si chaque point de A est identifié à un vecteur de E par l'isométrie précédente.
DémonstrationL'analyse des quadriques montre que, dans un repère quelconque une sphère s'exprime par l'équation d'une quadrique (cf l'article associé).
Réciproquement, si l'équation d'une quadrique dans le repère Rep est celle d'un compact non réduit à un point, alors il existe un repère Rep' de centre O, le centre de la quadrique tel que, si (yi) sont les coordonnées d'un point dans ce repère, l'équation s'écrive :
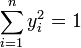
Soit B la base associée au repère Rep'. Soit P le produit scalaire qui confère le statut de base orthonormale à B. L'équation précédente montre que les points de la quadrique forment la sphère de rayon un pour P. Ceci montre l'existence recherchée.
Montrons l'unicité de P. Si P' est un autre produit scalaire ayant pour sphère unité la quadrique. Notons N (resp. N' ) la norme associée à P (resp. P' ). Soit x un vecteur quelconque de E, montrons que les deux normes sont confondues. Soit x un vecteur de E, x est le vecteur nul, alors les deux normes valent zéro et elles sont confondues pour ce vecteur. Sinon, les deux normes sont confondues sur la quadrique, donc :
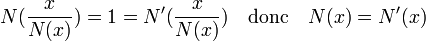
Les deux normes sont confondues, or le paragraphe précédent montre qu'une norme caractérise un produit scalaire, ce qui permet de conclure sur l'unicité.
Caractérisation par le groupe orthogonal
Article détaillé : Groupe orthogonal.Il existe enfin une caractérisation d'un espace euclidien par son groupe orthogonal. L'ensemble, noté GL(E), des automorphismes de E, c'est-à-dire des endomorphismes bijectifs, forme un groupe. De plus L(E) est un espace vectoriel de dimension finie, donc est naturellement muni d'une topologie, la norme utilisée est en général la norme d'opérateur. Le groupe orthogonal O(E) de E dispose donc d'une topologie naturelle, induite par celle de L(E) et telle que l'addition et la multiplication par un scalaire sont deux applications continues.
Proposition 1 — L'application de O(E)xO(E) dans O(E) qui, à deux automorphismes a et b associe le produit aob est une application infiniment différentiable. Il en est de même de l'application de O(E) dans lui-même, qui à a associe son inverse.
Le groupe orthogonal est donc muni d'une topologie induite compatible avec sa loi de composition et le passage à l'inverse. Une telle structure porte le nom de groupe de Lie. Un isomorphisme de groupe de Lie est un morphisme de groupe bijectif, continu et infiniment différentiable ainsi que son inverse.
Proposition 2 — Considérons deux produits scalaires sur des espaces vectoriels de même dimension. Il existe un isomorphisme de groupe de Lie du groupe orthogonal associé au premier produit scalaire dans le groupe orthogonal associé au deuxième produit scalaire.
Ainsi, un groupe de Lie d'automorphismes caractérise une géométrie euclidienne, au sens où pour une dimension donnée, ils sont tous les mêmes, à un isomorphisme près. Pour cette raison, on l'appelle souvent O(n). La proposition suivante montre que la caractérisation est plus profonde :
Proposition 3 — Soit E un espace vectoriel réel de dimension n et G un groupe d'automorphismes isomorphe au sens des groupes de Lie à O(n). Alors il existe un unique produit scalaire, à une homothétie près, tel que G soit son groupe des automorphismes.
On remarque que si <x, y> est un produit scalaire et λ un réel non nul, alors le produit scalaire <λx, λy> est possède le même groupe orthogonal que celui de <x, y>. Pour cette raison, il est nécessaire de préciser à une homothétie près.
À la différence des caractérisations précédentes, la méthode utilisée ici est relativement générique. Elle s'applique aux espaces affines euclidiens, aux géométries projectives ou encore symplectiques.
Démonstrations-
- L'application de O(E)xO(E) dans O(E) qui, à deux automorphismes a et b associe le produit aob est une application infiniment différentiable :
Soit a, b, h et k quatre automorphismes orthogonaux et p l'application produit, les propriétés du produit scalaire montre que :
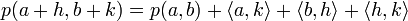
Le dernier terme vérifie la propriété suivante :

La différentielle est une application linéaire. La différentielle seconde de p est la différentielle d'une application linéaire, c'est une fonction constante qui à un point (a, b) associe l'application linéaire. Les autres différentielles existent et sont toutes nulles.
-
- L'application de O(E) lui-même qui, à un automorphisme a associe l'inverse a-1 est une application infiniment différentiable :
Soit a et h deux automorphismes de O(E) tel que la norme de h soit strictement inférieure à celle de a-1/2, alors si Id désigne l'automorphisme identité :
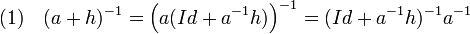
De plus :
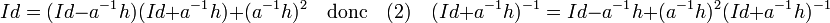
En utilisant les égalités (1) et (2), on obtient :
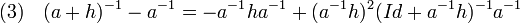
Majorons alors la norme du terme de droite de la dernière égalité, en remarquant que la norme de a-1h est inférieure à un demi :
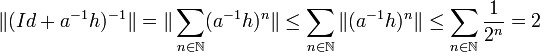
L'égalité (3) et la majoration précédente montre que :
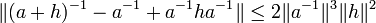
On en déduit que l'application inv qui à a associe a-1 est différentiable de différentielle au point a donnée par :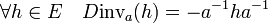
La différentielle au point est une composée d'applications différentiables, elle est donc différentiable. Par récurrence on montre que cette application est infiniment différentiable.
-
- Il existe un isomorphisme de groupe de Lie du groupe orthogonal associé au premier produit scalaire dans le groupe orthogonal associé au deuxième produit scalaire.
Soit E le premier espace et F le second. Soit a une isométrie de E dans F, c'est-à-dire une application qui préserve les produits scalaires. On remarque que a est bijectif car l'image d'une base orthonormale est une base orthonormale :
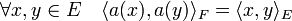
Considérons alors l'application φa de O(E) dans O(F) définie par :

L'application φ a bien son image dans O(F), est un morphisme de groupe, infiniment différentiable d'après la proposition précédente et inversible car ayant pour inverse l'application qui à a associe φa-1.
-
- Il existe un unique produit scalaire tel que G soit son groupe des automorphismes à une homothétie près :
La démonstration de ce résultat suppose l'utilisation de la théorie de la représentation des groupes de Lie, qui dépasse le cadre de cet article. Une démonstration est donc proposée uniquement en dimension deux. Le groupe O(R2) contient deux composantes connexes le sous-groupe des rotations SO(R2) et celui des symétries. Le groupe SO(E) est isomorphe au groupe multiplicatif des complexes de module un. Notons G+ la composante connexe de G isomorphe à SO(R2) et donc aux complexes de module un. Et soit φ un isomorphisme du groupe des complexes de module un dans G+, un sous-groupe de GL(E) le groupe des automorphismes. L'objectif est de montrer que l'image de φ est égale au groupe des rotations pour un produit scalaire bien choisi. Montrons tout d'abord la proposition suivante :
-
- Tout élément de G+ possède un déterminant strictement positif.
La suite de la démonstration montrera que le déterminant de tout élément de G+ est en fait égal à un. L'application detoφ est une application positive, son image par le point un est égale à un car l'image de l'élément neutre d'un groupe est l'élément neutre du groupe d'arrivée et que le déterminant de l'identité est égal à un. L'application detoφ ne s'annule jamais car un élément de G+ est inversible, son ensemble de départ est connexe et son ensemble d'arrivée contient un, ce qui démontre la proposition.
-
- L'image de -1 par φ est égale à moins l'identité :
On remarque que φ(-12) est égal à l'identité donc φ(-1)2 - Id est égal à zéro. Le polynome annulateur de φ(-1) est scindé sans racine double, il existe une base de vecteurs propres de valeurs propres associées 1 ou -1. Si l'espace propre associé à la valeur propre 1 est de dimension deux, alors φ(-1) est égal à l'identité et φ n'est pas injectif, ce qui est contraire aux hypothèses. Si l'espace propre associé à la valeur propre 1 est de dimension un, alors le déterminant de φ(-1) est négatif, ce qui est contraire à la proposition précédente. En conclusion, cet espace propre est de dimension zéro, ce qui démontre que φ(-1) est égal à -Id.
-
- Construction de la base qui apparaîtra plus tard comme orthonormale :
Soit iE l'image de i l'imaginaire pur par φ et e1 un vecteur non nul de E. Définissons e1 comme l'image de e1 par iE. Montrons alors que (e1, e2) est une base de E. Il suffit de montrer que les deux vecteurs sont libres ou encore que le premier n'est pas un vecteur propre. L'isomorphisme φ nous apprend que iE2 est égal à -Id ou encore que X2 + 1 est un polynôme annulateur de iE. Il n'admet pas de racine réelle, ce qui montre que iE n'est pas diagonalisable et termine la démonstration de cette proposition.
On remarque que iE(e1) et égal à e2, iE(e2) est égal à l'image de e1 par le carré de iE c'est-à-dire -Id et donc -e1.
-
- L'image des nombres diadiques par l'application eE définie par l'égalité suivante est incluse dans G+ :
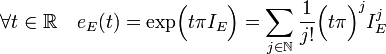
La définition de l'exponentielle d'un endomorphisme est donnée dans l'article Diagonalisation. Un nombre diadique est un nombre rationnel tel que le dénominateur est une puissance de deux, il est donc de la forme k/2n avec k un entier et n un entier positif.
Il suffit de montrer la proposition pour k égal à un. En effet, la stabilité par la composition démontre alors le résultat pour k quelconque car :
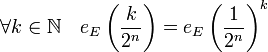
Démontrons ce résultat par récurrence sur n.
Montrons ce résultat pour n égal à un. On remarque que l'espace vectoriel engendré par les automorphismes Id et iE forment une algèbre A avec la loi de composition interne des automorphismes. De plus A dispose d'une structure de corps, l'application linéaire ψ de C l'ensemble des nombres complexes dans A ayant pour image de la base (1, i ) la base (Id, iE) est un isomorphisme d'algèbre, on en déduit :
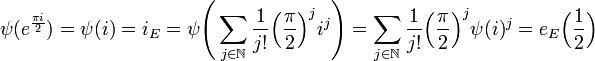
Supposons ce résultat vrai pour p et montrons le pour p + 1. Notons ζn l'image de 2-n par eE. L'isomorphisme ψ montre que eE est un morphisme du groupe des réels muni de l'addition vers G+. On en déduit que ζp+12 est égal à ζp.
L'équation x2 = a admet deux solutions opposées dans le cercle unité des complexes si a est un nombre complexe de module un. En conséquence l'équation x2 = a admet deux solutions opposées dans G+. Il reste à savoir si cette équation x2 = a admet uniquement deux solutions à déterminant positif dans GL(E). Nous savons que a est ici un carré, l'équation s'écrit donc x2 = b2 ou encore y2 = Id avec le changement de variable y = b-1x. Il a été précédemment démontré qu'une telle équation n'admet que deux solutions à déterminant positif Id et -Id. En conclusion, il n'existe qu'une racine carrée de ζp à déterminant positif et proche de Id (l'autre solution est proche de -Id). Cette solution est donc nécessairement égale à l'image de 2-p-1 par eE et élément du groupe G+.
-
- Le groupe G+ est l'image de R par l'application eE.
Le groupe G+ est homéomorphe au cercle unité de C, il est donc complet. Il contient l'image d'un ensemble dense dans R, les nombres diadiques et eE est une application uniformément continue, il est donc possible de compléter eE sur l'ensemble des réels.
-
- Le produit scalaire <. , .> défini par la base orthonormale (e1, e2) possède pour groupe spécial orthogonal (le sous-groupe de déterminant égal à un) G+ :
Il suffit de remarquer que la matrice de eE(t) dans la base (e1, e2) est :
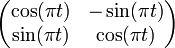
Pour s'en rendre compte, il suffit de remarquer que :
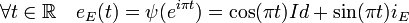
Topologie
Article détaillé : Topologie d'un espace vectoriel de dimension finie.Le produit scalaire définit une norme et donc une distance, conférant ainsi une structure d'espace métrique et topologique à l'ensemble. Cette structure est compatible avec les deux opérations que sont l'addition et la multiplication externe par un scalaire, c'est-à-dire que ces deux opérations sont continues.
Les espaces vectoriels réels de dimension finie n'admettent qu'une unique topologie séparée vérifiant cette compatibilité. Une formulation équivalente est que la norme euclidienne est équivalente à toutes les normes, euclidiennes ou non. La structure topologique d'un espace vectoriel normé de dimension finie E possède de nombreuses propriétés :
-
- Toute application linéaire de E dans un espace vectoriel normé est continue.
- E est uniformément homéomorphe à Rn.
- Les sous-espaces vectoriels de E sont des fermés.
- complétude : E est un espace complet, ainsi que l'ensemble des applications linéaires continues d'un espace vectoriel normé dans E.
- compacité : les compacts de E sont les fermés bornés. Toute boule fermée de E est compacte (voir théorème de Riesz). Réciproquement, un espace vectoriel normé dans lequel toute boule fermée est compacte est de dimension finie.
Généralisations
Il existe plusieurs généralisations des espaces euclidiens. En choisissant comme corps de base le corps des nombres complexes, on obtient la notion d'espace hermitien. De tels espaces admettent une théorie analogue, au prix d'adaptations naturelles : les résultats présentés dans cet article restent intégralement vérifiés pour ces espaces.[4]
En dimension infinie, une définition analogue (existence d'un produit scalaire ou hermitien) amène d'abord à la notion de préhilbertien, dans le cas réel et dans le cas complexe. Le caractère complet n'est pas vérifié en général. Un espace préhilbertien, complet pour la topologie d'espace métrique induite par la norme préhilbertienne, est appelé espace de Hilbert. Les espaces de Hilbert font l'objet d'une riche théorie, et sont des objets de base en analyse fonctionnelle[5].
Une géométrie euclidienne est définie par un espace vectoriel et une forme bilinéaire particulière (définie positive). Travailler avec certaines autres formes bilinéaires permet d'obtenir d'autres géométries, par exemple la géométrie symplectique.
Pour d'autres corps de base que les réels ou les complexes, la notion de forme bilinéaire définie positive n'est en général pas pertinente, car le corps n'est pas ordonné. On remplace généralement cette hypothèse par le fait que la forme est non dégénérée, c'est-à-dire qu'il n'existe pas de vecteur non nul orthogonal à tout l'espace. Une telle structure est utilisée, par exemple pour la géométrie sur les groupes finis. Les groupes orthogonaux sur des espaces vectoriels de dimension finie sur les corps finis fournissent notamment des familles infinies de groupes simples[6].
Références
Notes
- ↑ Une approche de cette nature se trouve dans : Y. Ladegaillerie Géométrie pour le CAPES de mathématiques Ellipses Marketing 2002 (ISBN 2729811486)
- ↑ C Antonini J F Quint P Borgnat J Bérard E Lebeau E Souche A Chateau O Teytaud Espace préhilbertien réel par le site les mathématiques.net
- ↑ Le terme d'espace vectoriel canonique pour Rn est largement utilisé, on peut citer : R. Godement Domaines fondamentaux des groupes arithmétiques Séminaire Bourbaki Tome 8 1962 à 1964 Exposé n° 257
- ↑ Cette généralisation est traitée par exemple dans Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions].
- ↑ Cette généralisation est traitée par exemple dans : Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] p 78 à 116.
- ↑ Une référence standard mais technique : R. W. Carter Simple Groups of Lie Type John Wiley & Sons Ltd., Chichester, 1993 (ISBN 0-471-50683-4)
Liens externes
- (fr) Espaces euclidiens un cours niveau Maths PCSI par S. Gonnord
- (fr) Espaces euclidiens par les mathématiques.net C.Antonini, J.F. Quint, P. Borgnat, J. Bérard, E. Lebeau, E. Souche, A. Chateau, O. Teytaud 2001
- (fr) Espace euclidien de Ross Moore de Macquarie University de Sydney traduit par Abderemane Morame de l'Université de Nantes 2006.
- (fr) Espaces euclidiens par F. Wlazinski de l'université de Picardie
Références
- J. M. Monier Cours de mathématiques - MPSI, PCSI, PTSI et MP, PSI , PC, PT Tome 8 : Algèbre et géométrie MP Dunod 5ème Ed 2007 (ISBN 9782100510382)
- J. Lelong-Ferrand, J. M. Arnaudiès Cours de mathématiques Tome 3 : Géométrie et cinématique Dunod 1977 (ISBN 9782100057160)
- E. Ramis, C. Deschamps, J. Odoux Cours de mathématiques, tome 5 : Applications de l'analyse à la géométrie Dunod 1998 (ISBN 2100041789)
- Portail des mathématiques
Catégories : Algèbre bilinéaire | Géométrie euclidienne -
Wikimedia Foundation. 2010.
