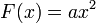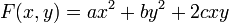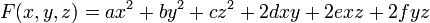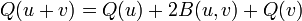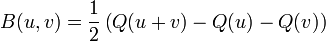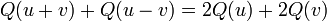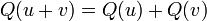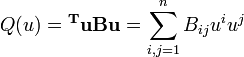- Forme Quadratique
-
Forme quadratique
En mathématiques, une forme quadratique est un polynôme homogène de degré deux avec un nombre quelconque de variables. Par exemple, la distance comprise entre deux points dans un espace euclidien à trois dimensions s'obtient en calculant la racine carrée d'une forme quadratique impliquant six variables qui sont les trois coordonnées de chacun des deux points.
Les formes quadratiques d'une, deux et trois variables sont données par les formules suivantes :
L'archétype de forme quadratique est la forme
 sur
sur 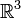 qui définit la structure euclidienne. C'est pourquoi la théorie des formes quadratiques utilise la terminologie de la géométrie (orthogonalité). La géométrie est un bon guide pour aborder cette théorie, malgré quelques pièges.
qui définit la structure euclidienne. C'est pourquoi la théorie des formes quadratiques utilise la terminologie de la géométrie (orthogonalité). La géométrie est un bon guide pour aborder cette théorie, malgré quelques pièges.Les formes quadratiques interviennent dans de nombreux domaines des mathématiques :
- La classification des coniques et plus généralement des quadriques projectives équivaut essentiellement à celle des formes quadratiques sur l'espace vectoriel correspondant.
- Si
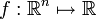 est une fonction
est une fonction 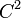 , la partie d'ordre 2 de son développement de Taylor, disons en 0, définit une forme quadratique.
, la partie d'ordre 2 de son développement de Taylor, disons en 0, définit une forme quadratique.
Si 0 est un point critique, cette forme, dans le cas où elle est non dégénérée, permet de décider si on a affaire à un maximum local, à un minimum local ou à un point selle.
- Les formes quadratiques interviennent en Mécanique du solide (ellipsoïde d'inertie) et en Statistique (analyse en composantes principales).
- Les formes quadratiques interviennent pour la résolution d'équations diophantiennes, Joseph-Louis Lagrange les utilise pour la démonstration du théorème des deux carrés de Fermat.
Sommaire
Formes quadratiques sur un espace vectoriel
Soit un espace vectoriel V sur un corps F. Pour l'instant, nous supposons que F possède une caractéristique différente de 2. C'est le cas, en particulier, pour les corps réels et complexes qui sont de caractéristique 0. Le cas où la caractéristique vaut 2 sera traité séparément.
Une application Q :
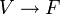 est appelée forme quadratique sur V s'il existe une forme bilinéaire symétrique B :
est appelée forme quadratique sur V s'il existe une forme bilinéaire symétrique B : 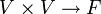 telle que
telle queB est appelée la forme bilinéaire associée. Si
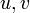 sont des vecteurs de V,
sont des vecteurs de V,donc nous pouvons retrouver la forme bilinéaire B à partir de Q :
C'est un exemple de polarisation d'une forme algébrique. Il existe alors une correspondance bijective entre les formes quadratiques sur V et les formes bilinéaires symétriques sur V. À partir d'une forme donnée, nous pouvons définir de manière unique l'autre forme.
Quelques autres propriétés des formes quadratiques :
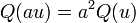
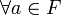 et
et 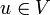
- Q obéit à la règle du parallélogramme :
- Les vecteurs u et v sont orthogonaux par rapport à B ssi
- Pour toute forme quadratique, il existe une base orthogonale, c'est à dire
une base
 telle que
telle que  pour
pour 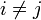 . C'est une conséquence immédiate de la réduction de Gauss.
. C'est une conséquence immédiate de la réduction de Gauss.Expression matricielle
Si V est de dimension n, et si
 est une base de V, on associe à B la matrice symétrique B définie par
est une base de V, on associe à B la matrice symétrique B définie par 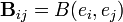 p. La forme quadratique Q est alors donnée par
p. La forme quadratique Q est alors donnée paroù les
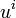 sont les coordonnées de u dans cette base, et u la matrice colonne formée par ces coordonnées. On dit que B est la matrice de Q par rapport à la base.
sont les coordonnées de u dans cette base, et u la matrice colonne formée par ces coordonnées. On dit que B est la matrice de Q par rapport à la base.Q(u) est un polynôme homogène de degré deux par rapport aux coordonnées de u, conformément à notre définition de départ.
Soit
 une autre base de V, et soit
une autre base de V, et soit  la matrice de passage exprimant les anciennes coordonnées en fonction des nouvelles. De la relation
la matrice de passage exprimant les anciennes coordonnées en fonction des nouvelles. De la relation 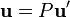 on tire
on tire 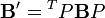 pour la matrice de B dans la nouvelle base. On dit que B et B' sont congruentes.
pour la matrice de B dans la nouvelle base. On dit que B et B' sont congruentes.Rang
Le noyau d'une forme quadratique Q ( on dit aussi radical) est par définition le sous-espace vectoriel
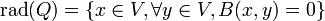
Cet espace est le noyau de l'application linéaire de V dans l'espace dual V* qui associe à x la forme linéaire
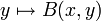 Une forme quadratique est dite non dégénérée si rad(Q)=0, autrement dit si l'application linéaire ci-dessus est un isomorphisme.
Une forme quadratique est dite non dégénérée si rad(Q)=0, autrement dit si l'application linéaire ci-dessus est un isomorphisme.Le rang de Q est par définition dim V - dim(rad(Q)). C'est aussi le rang de la matrice de Q par rapport à une base quelconque.
Sous-espaces orthogonaux
Si W est un sous-espace vectoriel de V, l'orthogonal de W est le sous-espace
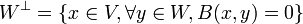
Cette notion généralise l'orthogonalité dans les espaces euclidiens, mais il y a quelques pièges. Par exemple sur
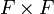 , la forme quadratique
, la forme quadratique 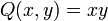 est non dégénérée, mais chacun des sous-espaces
est non dégénérée, mais chacun des sous-espaces 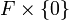 et
et 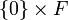 est son propre orthogonal. Plus généralement, si Q est non dégénérée, on a bien
est son propre orthogonal. Plus généralement, si Q est non dégénérée, on a bien 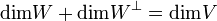 , comme dans le cas euclidien. Mais l'intersection
, comme dans le cas euclidien. Mais l'intersection 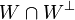 n'est pas forcément réduite à zéro.
n'est pas forcément réduite à zéro.Discriminant
Soit q une forme quadratique et A sa matrice par rapport à une base de V. Si l'on effectue un changement de base de matrice Q, la matrice de q dans la nouvelle base sera
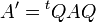 . D'après les propriétés élémentaires des déterminants,
. D'après les propriétés élémentaires des déterminants,  . Si q est non dégénérée, l'image du déterminant dans le groupe quotient
. Si q est non dégénérée, l'image du déterminant dans le groupe quotient 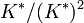 ne dépend pas de la base. C'est cet élément que l'on appelle le discriminant de la forme quadratique. Si q est dégénérée, on convient que le discriminant est nul.
ne dépend pas de la base. C'est cet élément que l'on appelle le discriminant de la forme quadratique. Si q est dégénérée, on convient que le discriminant est nul.Exemples
- Corps des complexes
Si
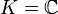 , le quotient
, le quotient 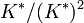 est réduit à l'élément neutre, et le discriminant est sans intérêt.
est réduit à l'élément neutre, et le discriminant est sans intérêt.- Corps des réels
Si
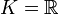 , le quotient
, le quotient 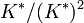 s'identifie à
s'identifie à 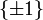 , vu comme sous-groupe multiplicatif de
, vu comme sous-groupe multiplicatif de 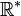 . On peut donc parler de formes quadratiques à discriminant positif ou négatif. Par exemple, le discriminant de la forme quadratique ax2 + 2bxy + cy2 sur
. On peut donc parler de formes quadratiques à discriminant positif ou négatif. Par exemple, le discriminant de la forme quadratique ax2 + 2bxy + cy2 sur 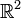 , supposée non dégénérée, est donnée par le signe de
, supposée non dégénérée, est donnée par le signe de 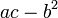 . S'il est positif, la forme est définie positive ou définie négative, s'il est négatif, la réduction de Gauss sera de la forme
. S'il est positif, la forme est définie positive ou définie négative, s'il est négatif, la réduction de Gauss sera de la forme 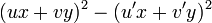 . On retrouve, ce qui n'est pas surprenant, la théorie de l'équation du second degré.
. On retrouve, ce qui n'est pas surprenant, la théorie de l'équation du second degré.- Corps finis
Si p est un nombre premier, et K le corps
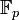 à p éléments, la théorie élémentaires des résidus quadratiques assure que
à p éléments, la théorie élémentaires des résidus quadratiques assure que 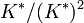 est encore isomorphe au groupe à deux éléments.
est encore isomorphe au groupe à deux éléments.Le problème de classification
On dira que deux formes quadratiques Q et Q' sont équivalentes s'il existe une application linéaire inversible
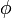 telle que
telle que 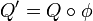 . Il revient au même de dire que leur matrices dans une même base sont congruentes. Classer les formes quadratiques sur un espace vectoriel V c'est
. Il revient au même de dire que leur matrices dans une même base sont congruentes. Classer les formes quadratiques sur un espace vectoriel V c'est- déterminer les classes d'équivalence de la relation précédente (qui est clairement une relation d'équivalence)
- déterminer les orbites de l'ensemble des formes quadratiques sous l'action du groupe linéaire
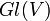 donnée par
donnée par 
(ce ne sont que deux façons d'exprimer la même chose).
On a les résultats suivants.
- Si V est un espace vectoriel de dimension finie sur un corps F algébriquement clos
(de caractéristique
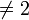 ) deux formes quadratiques sont équivalentes si et seulement si elles ont même rang. C'est une conséquence directe de la réduction de Gauss
) deux formes quadratiques sont équivalentes si et seulement si elles ont même rang. C'est une conséquence directe de la réduction de Gauss- Si V est un espace vectoriel de dimension finie sur
 ,
,
deux formes quadratiques sont équivalentes si et seulement si elles ont même rang et même signature (loi d'inertie de Sylvester).
Deux formes quadratiques équivalentes ont même rang et même discriminant, mais l'inverse est loin d'être en général vrai.
Cas de corps de caractéristique deux
La théorie des formes quadratiques de caractéristique deux possède une petite saveur différente, essentiellement parce que la division par 2 n'est pas possible. Il n'est plus vrai non plus que chaque forme quadratique est de la forme Q(u) = B(u,u) pour une forme bilinéaire symétrique B. En outre, même si B existe, elle n'est pas unique : puisque les formes alternées sont aussi symétriques en caractéristique deux, on peut ajouter toute forme alternée à B et obtenir la même forme quadratique.
Une définition plus générale d'une forme quadratique qui marche pour toute caractéristique est la suivante. Une forme quadratique d'un espace vectoriel V sur un corps F est comme une application
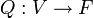 telle que
telle que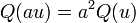
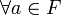 et
et 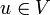 , et
, et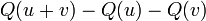 est une forme bilinéaire sur V.
est une forme bilinéaire sur V.
Généralisations
On peut généraliser la notion de forme quadratique à des modules sur un anneau commutatif. Les formes quadratiques entières sont importantes en théorie des nombres et topologie.
Liens internes
- matrice
- réduction de Gauss
- matrice définie positive
- loi d'inertie de Sylvester
- Première forme fondamentale
- Seconde forme fondamentale
Références
- M. Berger, Cours de Géométrie
- J.P. Serre, Cours d'Arithmétique, Presses Universitaires de France 1970
Articles de mathématiques en rapport avec l'algèbre bilinéaireEspace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz
- Portail des mathématiques
Catégorie : Algèbre bilinéaire
Wikimedia Foundation. 2010.