- Elements d'Euclide
-
Éléments d'Euclide
Les Éléments (en grec ancien Στοιχεία / Stoikheía) sont un traité mathématique et géométrique, constitué de 13 livres organisés thématiquement, probablement écrit par le mathématicien grec Euclide vers 300 av. J.-C. Il comprend une collection de définitions, axiomes, théorèmes et leur démonstration sur les sujets de la géométrie euclidienne et de la théorie des nombres primitive.
Les Éléments sont le plus ancien exemple connu d'un traitement axiomatique et systématique de la géométrie et son influence sur le développement de la logique et de la science occidentale est fondamentale. Il s'agit probablement du recueil qui a rencontré le plus de succès au cours de l'Histoire : les Éléments furent l'un des premiers livres imprimés (Venise, 1482) et n'est précédé que par la Bible pour le nombre d'éditions publiées (largement plus de 1 000). Pendant des siècles, il a fait partie du cursus universitaire standard.
Sommaire
Principes
La méthode d'Euclide a consisté à baser ses travaux sur des définitions, des "demandes" (postulats) , des « notions ordinaires » (axiomes), et des propositions (problèmes résolus). Par exemple, le livre I contient 35 définitions (point, ligne, surface, etc.), cinq postulats et cinq notions ordinaires.
Postulats du livre I :
- Un segment de droite peut être tracé en joignant deux points quelconques.
- Un segment de droite peut être prolongé indéfiniment en une ligne droite.
- Etant donné un segment de droite quelconque, un cercle peut être tracé en prenant ce segment comme rayon et l'une de ses extrémités comme centre.
- Tous les angles droits sont congruents.
- Si deux lignes sont sécantes avec une troisième de telle façon que la somme des angles intérieurs d'un côté est inférieure à deux angles droits, alors ces deux lignes sont forcément sécantes de ce côté.
Notions ordinaires du livre I :
- Des choses qui sont égales à une même chose sont égales entre elles.
- Si des choses égales sont ajoutées à d'autres choses égales, leurs sommes sont égales.
- Si des choses égales sont soustraites à d'autres choses égales, les restes sont égaux.
- Des choses qui coïncident avec une autre sont égales entre elles.
- Le tout est plus grand que la partie.
Postérité
Le succès des Éléments est dû principalement à la présentation logique de la quasi-totalité du savoir mathématique dont Euclide disposait. L'utilisation systématique et efficace du développement des démonstrations à partir d'un jeu réduits d'axiomes incita à les utiliser comme livre de référence pendant des siècles.
Tout au long de l'Histoire, quelques controverses entourèrent les axiomes et les démonstrations d'Euclide. Néanmoins, les Éléments restent une œuvre fondamentale dans l'histoire des sciences et furent d'une influence considérable. Les scientifiques européens Nicolas Copernic, Johannes Kepler, Galileo Galilei et particulièrement Isaac Newton furent tous influencés par les Éléments et appliquèrent leur connaissance du livre à leur propre travaux. Certains mathématiciens (Bertrand Russell, Alfred North Whitehead) et philosophes (Baruch Spinoza) ont également tenté d'écrire leur propres Éléments, des structures déductives axiomatiques appliquées à leurs disciplines respectives.
Dans cinq postulats énoncés dans le livre I, le dernier, dont on déduit le postulat des parallèles : « en un point extérieur à une droite, ne passe qu'une unique droite qui lui est parallèle », a toujours semblé moins évident que les autres. Plusieurs mathématiciens soupçonnèrent qu'il pouvait être démontré à partir des autres postulats, mais toutes les tentatives pour ce faire échouèrent. Vers le milieu du XIXe siècle, il fut démontré qu'une telle démonstration n'existe pas, que le cinquième postulat est indépendant des quatre autres et qu'il est possible de construire des géométries non-euclidiennes cohérentes en prenant sa négation.
Histoire
Les premières traces écrites des notions de longueurs et d'orthogonalité sont babyloniennes et remontent à une période située entre 1900 et 1600 av. J.-C.[1]. On y trouve la connaissance du théorème de Pythagore au moins pour le cas d'un triangle dont les cotés sont de longueurs respectives trois, quatre et cinq.
La première formalisation est rassemblée dans un livre appelé Les Éléments. Il contient tout le savoir mathématique de l'époque. Bien que la plupart des théorèmes leur soient antérieurs, les Éléments étaient suffisamment complets et rigoureux pour éclipser les œuvres géométriques qui les ont précédés et peu de choses sont connues sur la géométrie pré-euclidienne.
Son auteur Euclide d'Alexandrie (325-265 av. J.-C.) est un mathématicien grec qui fut probablement un disciple d'Aristote (-384-322 av. J.-C.). Son histoire ainsi que celle de ce livre sont mal connues. Trois hypothèses sont avancées à son sujet. Euclide est:
-
- soit un personnage historique principal auteur des Eléments,
- soit à la tête d'une école mathématique
- soit un nom d'auteur qu'a utilisé un groupe de mathématiciens pour rédiger une compilation, ce nom serait alors une référence au philosophe grec Euclide de Mégare (450-380 av. J.-C.) [2].
Si la première hypothèse a été admise sans l'ombre d'un doute pendant plus de 2000 ans, elle reste encore la plus vraisemblable. En revanche, il est pratiquement établi qu'Euclide était à la tête d'une école mathématique vigoureuse et ses disciples ont certainement contribué à la rédaction [3] des Eléments. Hippocrate de Chios (470-410 av. J.-C.) est l'auteur du contenu des livres I et II des éléments, si on en croit le philosophe byzantin Proclos (411-487). Il écrit de lui « Il était le premier à écrire pour la compilation maintenant connue sous le nom des Eléments » [4].
L'ouvrage fut traduit en arabe après avoir été donné aux Arabes par l'Empire byzantin, puis traduit en latin d'après les textes arabes (Adelard de Bath au XIIe siècle, repris par Campanus de Novare). La première édition imprimée date de 1482 et le livre fut depuis traduit dans une multitude de langues et publié dans plus de 1 000 éditions différentes. Des copies du texte grec existent toujours, par exemple dans la bibliothèque du Vatican ou à la Bodleian Library à Oxford, mais ces manuscrits sont de qualité variable et toujours incomplets. Par analyse des traductions et des originaux, il a été possible d'émettre des hypothèses sur le contenu originel, dont il ne subsiste aucune copie intégrale.
Axiomatisation ultérieure
Les mathématiciens du XIXe siècle découvrirent que les démonstrations d'Euclide nécessitent des hypothèses additionnelles, non spécifiées dans le texte original. David Hilbert modifia la liste pour en fournir un jeu complet en 1899 dans un article intitulé Les fondements de la géométrie. La liste des axiomes de Hilbert en contient 20.
Livres
Les Éléments sont organisés comme suit :
- Les livres I à IV traitent de géométrie plane :
- Le livre I énonce les propriétés de base de la géométrie : théorème de Pythagore, égalités angulaires et d'aires et parallélisme, somme des angles du triangle, les trois cas d'égalité des triangles.
- Le livre II est couramment nommé livre de l'algèbre géométrique, parce qu'il est un livre de géométrie facile à interpréter comme de l'algèbre, ce qu'il n'est pas exactement mais il a été compris et utilisé en mathématiques arabes pour l'algèbre. En particulier, les théorèmes qu'il énonce correspondent en grande partie à nos identités remarquables. Un cas particulier d'un problème correspondant à une équation du second degré est également donné.
- Le livre III traite du cercle et de ses propriétés : angle inscrit, puissance d'un point, tangente.
- Le livre IV s'occupe de l'inscription et de la circonscription de triangles ou de polygones réguliers dans le cercle.
- Les livres V à X font intervenir les proportions :
- Le livre V est le traité des proportions de grandeurs.
- Le livre VI est celui de l'application des proportions à la géométrie : théorème de Thalès, figures semblables.
- Le livre VII est consacré à l'arithmétique : divisibilité, nombres premiers, PGCD, PPCM.
- Le livre VIII traite de l'arithmétique des proportions et des suites géométriques.
- Le livre IX applique les précédents : infinité des nombres premiers, somme d'une suite géométrique, nombres parfaits.
- Le livre X est une tentative de classification des grandeurs irrationnelles. L'irrationalité de
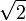 y est démontrée.
y est démontrée.
- Les livres XI à XIII traitent de géométrie dans l'espace :
- Le livre XI généralise dans l'espace les livres I à VI : perpendicularité, parallélisme, volumes de parallélépipèdes.
- Le livre XII compare ou calcule des aires et volumes en utilisant la méthode d'exhaustion : disque, cônes, pyramides, cylindres et sphère.
- Le livre XIII est la généralisation du livre IV dans l'espace : section dorée, les cinq polyèdres réguliers inscrits dans une sphère.
Il existe deux livres apocryphes, présents en annexe dans la traduction de Heath.
Références
- ↑ la tablette 322 de la collection de G A Plimpton conservée à l'université de Columbia.
- ↑ J Itard, Les livres arithmétique d'Euclide (Paris, 1962)
- ↑ Biographie d'Euclide dans Dictionary of Scientific Biography (New York 1970-1990)
- ↑ T L Heath, A History of Greek Mathematics I (Oxford, 1921), 182-202
Voir aussi
Articles connexes
Liens externes
- Euclide. Les quinze livres des éléments géométriques d'Euclide : plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant, traduction de 1632, site Gallica
- (en) Euclid's Elements adapté pour Internet par D. E. Joyce
- (en) Oliver Byrne's edition of Euclid (version en couleurs)
- The Elements of Euclid, by Isaac Todhunter - Wikisource
Bibliographie
- Les Éléments d'Euclide, traduction François Peyrard, éd. Blanchard Paris, 1993 (1re éd. 1819)
- Euclide, Les Éléments, traduction, commentaires et notes de Bernard Vitrac [détail des éditions]
Éléments d'Euclide Livre I ~ Livre II ~ Livre III ~ Livre IV ~ Livre V ~ Livre VI
Livre VII ~ Livre VIII ~ Livre IX ~ Livre X ~ Livre XI ~ Livre XII ~ Livre XIII- Portail des mathématiques
Catégories : Géométrie euclidienne | Livre historique de mathématiques | Mathématiques de l'Antiquité
Wikimedia Foundation. 2010.



