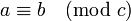- Theorie des nombres
-
Théorie des nombres
Traditionnellement, la théorie des nombres est une branche des mathématiques qui s'occupe des propriétés des nombres entiers, qu'ils soient entiers naturels ou entiers relatifs, et contient beaucoup de problèmes ouverts qu'il est facile de comprendre, même par les non-mathématiciens. Plus généralement, le champ d'étude de cette théorie concerne une large classe de problèmes qui proviennent naturellement de l'étude des entiers. La théorie des nombres occupe une place particulière en mathématiques, à la fois par ses connexions avec de nombreux autres domaines, et par la fascination qu'exercent ses énoncés. Ainsi, la citation suivante, de Jürgen Neukirch :
- « La théorie des nombres occupe parmi les disciplines mathématiques une position idéalisée analogue à celle qu'occupent les mathématiques elles-mêmes parmi les autres sciences. »[1]
Le terme « arithmétique » est aussi utilisé pour faire référence à la théorie des nombres. C'est un terme assez ancien, qui n'est plus aussi populaire que par le passé. Néanmoins, le terme reste répandu — c’est-à-dire dans les noms des champs mathématiques (géométrie algébrique arithmétique, l'arithmétique des courbes et surfaces elliptiques). Ce sens du terme arithmétique ne doit pas être confondu avec la branche de logique qui étudie l'arithmétique dans le sens des systèmes formels.
La théorie des nombres peut être divisée en plusieurs champs d'étude en fonction des méthodes utilisées et des questions traitées.
Article détaillé : liste des matières de la théorie des nombres.Sommaire
Les diverses branches de la théorie des nombres
La théorie élémentaire des nombres
Dans ce domaine, les entiers sont étudiés sans utiliser de techniques d'autres domaines des mathématiques. Les questions de divisibilité, l'algorithme d'Euclide pour calculer le plus grand commun diviseur (PGCD), la factorisation des entiers en nombres premiers, la recherche des nombres parfaits et des congruences appartiennent à ce domaine. Les affirmations typiques sont le petit théorème de Fermat et le théorème d'Euler, et par extension le théorème des restes chinois et la loi de réciprocité quadratique. Les propriétés des fonctions multiplicatives comme la fonction de Möbius et la fonction φ d'Euler sont étudiées ; ainsi que les suites d'entiers comme les factorielles et les nombres de Fibonacci.
Beaucoup de questions en théorie élémentaire des nombres apparaissent simples mais requièrent de très profondes considérations et de nouvelles approches, tels les exemples suivants :
- La conjecture de Goldbach concernant l'expression des nombres pairs comme somme de deux nombres premiers,
- La conjecture des nombres premiers jumeaux à propos de l'infinité des paires de nombres premiers consécutifs, et
- La conjecture de Syracuse concernant une simple itération.
La théorie des équations diophantiennes a même été montrée comme étant indécidable.
Article détaillé : problèmes de Hilbert.La théorie analytique des nombres
La théorie analytique des nombres emploie l'outillage du calcul infinitésimal et de l'analyse complexe pour traiter des questions sur les entiers. Le théorème des nombres premiers et l'hypothèse de Riemann qui lui est reliée en sont des exemples. Le problème de Waring (c’est-à-dire : pour un nombre donné, est-il la somme de carrés, de cubes, etc.), la conjecture des nombres premiers jumeaux (trouver infiniment beaucoup de paires de nombres premiers dont la différence est 2) et la conjecture de Goldbach (écrire les entiers pairs comme somme de deux nombres premiers) sont attaqués avec les méthodes d'analyse avec succès. Les preuves de la transcendance des constantes mathématiques, comme π ou e, sont aussi classées comme faisant partie de la théorie analytique des nombres. Tandis que les résultats à propos des nombres transcendants semblent être enlevés de l'étude des entiers, ils étudient réellement les valeurs possibles de polynômes à coefficients entiers évalué à, disons, e; ils sont aussi reliés fermement au champ de l'approximation diophantienne, qui recherche « de quelle façon correcte » un nombre réel donné peut être approximé par un nombre rationnel.
La théorie algébrique des nombres
Dans la théorie algébrique des nombres, le concept de nombre est étendu aux nombres algébriques qui sont les racines des polynômes avec des coefficients rationnels. Ces domaines contiennent des éléments analogues aux entiers, connus sous le nom entiers algébriques. Avec ces règles, les propriétés familières des entiers (c’est-à-dire la factorisation unique) ne sont plus les mêmes. Les vertus de l'outillage employé -- théorie de Galois, corps cohomologique, théorie des corps de classes, représentation des groupes et les fonctions L -- sont telles qu'elles permettent de retrouver un ordre partiel pour ces nouvelles classes de nombres.
Beaucoup de questions théoriques sur les nombres sont attaquées avec succès par leur étude modulo p pour tous les nombres premiers p.
Article détaillé : corps fini.Ceci est appelé localisation et mène à la construction des nombres p-adiques ; ce champ d'étude est appelé analyse locale et résulte de la théorie algébrique des nombres.
La théorie géométrique des nombres
Traditionnellement appelée géométrie des nombres, la théorie géométrique des nombres incorpore toutes les formes de la géométrie. Elle commence avec le théorème de Minkowski à propos de réseaux de points (treillis) dans les ensembles convexes et de recherches sur les empilement de sphères. La géométrie algébrique, et spécialement la théorie des courbes elliptiques, peuvent aussi être employées. Le célèbre Dernier théorème de Fermat fut prouvé avec ces techniques.
La théorie combinatoire des nombres
La théorie combinatoire des nombres s'occupe des problèmes de théorie des nombres qui impliquent les idées combinatoires dans leurs formulations ou leurs solutions. Paul Erdős est le principal fondateur de cette branche de la théorie des nombres. Les sujets caractéristiques incluent le système de couverture, les problèmes à somme zéro, diverses sommes d'ensembles restreintes et des progressions arithmétiques dans l'ensemble des entiers. Les méthodes algébriques ou analytiques sont puissantes dans ce champ d'étude.
La théorie calculatoire des nombres
Ce domaine étudie plus particulièrement les algorithmes appropriés pour la théorie des nombres. Les algorithmes déterministes et probabilistes pour les tests de primalité des nombres supposés premiers et les décompositions en produit de facteurs premiers de nombres à plusieurs centaines de chiffres ont d'importantes applications en cryptographie et est, de fait, un sujet très sensible.
Histoire de la théorie des nombres
Civilisation védique
Les mathématiciens de l'Inde se sont intéressés à la recherche de solutions intégrales solutions d'équations diophantiennes depuis la période védique. L'usage géométrique le plus ancien des équations diophantiennes peut être retracé dans les Sulba Sutras, qui ont été écrits entre le VIIIe et le VIe siècle av. J.-C. Baudhayana (env. 800 avant JC) trouva deux ensembles de solutions intégrales positives à un système d'équations diophantiennes, et utilisa aussi les systèmes d'équations diophantiennes à quatre inconnues. Apastamba (env. 600 avant JC) utilisa les systèmes d'équations diophantiennes à cinq inconnues.
Époque jaïna
En Inde, les mathématiciens de l'époque jaïna développèrent une théorie des nombres systématique du IVe siècle av. J.-C. jusqu'au IIe siècle av. J.-C. Le texte Surya Prajinapti (env. 400 avant JC) classe tous les nombres en trois ensembles : énumérables, non énumérables et infini. Chacun de ces trois ensembles était divisé plus avant en trois ordres :
- Énumérables : le plus bas, intermédiaire et le plus haut.
- Non énumérable : non énumérable proche, vraiment non énumérable et non énumérablement non énumérable.
- Infini : infini proche, vraiment infini, infiniment infini.
Les mathématiciens de l'époque jaïna furent les premiers à écarter l'idée que tous les infinis sont les mêmes ou égaux. Ils reconnurent cinq types différents d'infini : infini dans une ou deux directions (une dimension), infini en surface (deux dimensions), infini partout (trois dimensions), et infini perpétuellement (dans un nombre infini de dimensions).
Le nombre énumérable le plus haut N des ouvrages jaïnas correspond au concept moderne de aleph-zéro
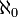 (le nombre cardinal de l'ensemble infini des entiers 1, 2, ...), le plus petit nombre transfini cardinal. Les mathématiciens de cette époque ont défini aussi un système entier de nombres cardinaux transfinis, dans lequel notre
(le nombre cardinal de l'ensemble infini des entiers 1, 2, ...), le plus petit nombre transfini cardinal. Les mathématiciens de cette époque ont défini aussi un système entier de nombres cardinaux transfinis, dans lequel notre 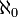 est le plus petit.
est le plus petit.Dans le travail sur la théorie des ensembles, deux types de nombres transfinis de base ont été distingués. Pour des raisons à la fois physiques et ontologiques, une distinction fut faite entre asmkhyata et ananata, entre infini rigidement lié et infini pauvrement lié.
Civilisation grecque
La théorie des nombres fut une étude favorite parmi les mathématiciens grecs d'Alexandrie, Égypte à partir du IIIe siècle av. J.-C., qui eurent conscience du concept d'équation diophantienne dans de nombreux cas particuliers. Le premier mathématicien hellène à étudier ces équations fut Diophante.
Diophante a également recherché une méthode pour trouver les solution entières pour les équations indéterminées linéaires, équations pour lesquelles il manque une information suffisante pour produire un ensemble unique de réponses discrètes. L'équation
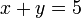 est une telle équation. Diophante a découvert que beaucoup d'équations indéterminées peuvent être ramenées à une forme où une certaine catégorie de solutions est connue alors qu'une solution spécifique ne l'est pas.
est une telle équation. Diophante a découvert que beaucoup d'équations indéterminées peuvent être ramenées à une forme où une certaine catégorie de solutions est connue alors qu'une solution spécifique ne l'est pas.L'époque classique en Inde
Les équations diophantiennes furent étudiées de manière intensive par les mathématiciens indiens de la période médiévale, qui furent les premiers à chercher systématiquement des méthodes pour la détermination de solutions intégrales d'équations diophantiennes. Aryabhata (en 499) donna la première description explicite de la solution intégrale générale de l'équation diophantienne linéaire
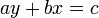 , qui apparaît dans son texte Aryabhatiya. Cet algorithme kuttaka est considéré comme étant l'une des contributions les plus significatives d'Aryabhata en mathématiques pures, qui trouva les solutions d'équations diophantiennes en termes de fractions continues. La technique fut appliquée par Aryabhata pour donner les solutions intégrales d'un système d'équations diophantiennes linéaires, un problème avec d'importantes applications en astronomie. Il trouva aussi la solution générale de l'équation linéaire indéterminée en utilisant cette méthode.
, qui apparaît dans son texte Aryabhatiya. Cet algorithme kuttaka est considéré comme étant l'une des contributions les plus significatives d'Aryabhata en mathématiques pures, qui trouva les solutions d'équations diophantiennes en termes de fractions continues. La technique fut appliquée par Aryabhata pour donner les solutions intégrales d'un système d'équations diophantiennes linéaires, un problème avec d'importantes applications en astronomie. Il trouva aussi la solution générale de l'équation linéaire indéterminée en utilisant cette méthode.Brahmagupta en 628 manipula des équations diophantiennes plus difficiles. Il utilisa la méthode chakravala pour résoudre les équations diophantiennes quadratiques, incluant des formes de l'équation de Pell-Fermat, telle que
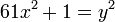 . Son Brahma Sphuta Siddhanta fut traduit en arabe en 773 et fut traduit plus tard en Latin en 1126. L'équation
. Son Brahma Sphuta Siddhanta fut traduit en arabe en 773 et fut traduit plus tard en Latin en 1126. L'équation 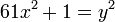 fut plus tard posée comme un problème en 1657 par le mathématicien français Pierre de Fermat. La solution générale de cette forme particulière d'équation de Pell-Fermat fut trouvée plus de 70 ans plus tard par Leonhard Euler, tandis que la solution générale de l'équation de Pell-Fermat fut trouvée plus de 100 ans plus tard par Joseph Louis Lagrange en 1767. En attendant, il y a beaucoup de siècles de cela, la solution générale de l'équation de Pell-Fermat fut enregistrée par Bhaskara II en 1150, utilisant une version modifiée de la méthode chakravala de Brahmagupta, qu'il utilisa aussi pour trouver la solution générale d'autres équations quadratiques intermédiaires indéterminées et des équations diophantiennes quadratiques. La méthode chakravala de Bhaskara pour trouver la solution générale de l'équation de Pell-Fermat était plus simple que la méthode utilisée par Lagrange 600 ans plus tard. Bhaskara trouva aussi des solutions pour d'autres équations indéterminées quadratiques, cubique, quartique et des équations polynômiales de degré plus élevés. Narayana Pandit perfectionna encore la méthode chakravala et trouva plus de solutions générales pour les autres indéterminées quadratiques ainsi que pour les équations polynômiales de degré plus élevés.
fut plus tard posée comme un problème en 1657 par le mathématicien français Pierre de Fermat. La solution générale de cette forme particulière d'équation de Pell-Fermat fut trouvée plus de 70 ans plus tard par Leonhard Euler, tandis que la solution générale de l'équation de Pell-Fermat fut trouvée plus de 100 ans plus tard par Joseph Louis Lagrange en 1767. En attendant, il y a beaucoup de siècles de cela, la solution générale de l'équation de Pell-Fermat fut enregistrée par Bhaskara II en 1150, utilisant une version modifiée de la méthode chakravala de Brahmagupta, qu'il utilisa aussi pour trouver la solution générale d'autres équations quadratiques intermédiaires indéterminées et des équations diophantiennes quadratiques. La méthode chakravala de Bhaskara pour trouver la solution générale de l'équation de Pell-Fermat était plus simple que la méthode utilisée par Lagrange 600 ans plus tard. Bhaskara trouva aussi des solutions pour d'autres équations indéterminées quadratiques, cubique, quartique et des équations polynômiales de degré plus élevés. Narayana Pandit perfectionna encore la méthode chakravala et trouva plus de solutions générales pour les autres indéterminées quadratiques ainsi que pour les équations polynômiales de degré plus élevés.La civilisation islamique
À partir du IXe siècle, les mathématiciens islamiques portèrent un vif intérêt a la théorie des nombres. Le premier de ces mathématiciens fut le mathématicien arabe Thabit ibn Qurra, qui découvrit un théorème qui permettait de trouver des paires de nombres amiables, c’est-à-dire deux nombres qui sont chacun la somme des diviseurs propres de l'autre.
Au Xe siècle, Al-Baghdadi découvrit une légère variante du théorème de Thabit ibn Qurra. Al-Haitham semble avoir été le premier à tenter de classer tous les nombres parfaits pairs (nombres égaux à la somme de leurs diviseurs propres) comme ceux de la forme
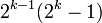 où
où 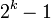 est premier. Al-Haytham est aussi la première personne à avoir établi le théorème de Wilson, concrètement que si p est premier alors
est premier. Al-Haytham est aussi la première personne à avoir établi le théorème de Wilson, concrètement que si p est premier alors 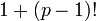 est divisible par
est divisible par 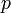 . Le fait n'est pas éclairci s'il savait comment démontrer ce résultat. Ce théorème porte le nom de théorème de Wilson à cause d'un commentaire fait par Edward Waring en 1770 dont John Wilson avait noté le résultat. John Wilson indique à Waring qu'il ne sait pas démontrer ce résultat, Waring ne trouve pas non plus de preuve. Pourtant la première démonstration connue provient de Leibniz, qui ne juge pas utile de la publier, et Euler en avait publié une preuve.
. Le fait n'est pas éclairci s'il savait comment démontrer ce résultat. Ce théorème porte le nom de théorème de Wilson à cause d'un commentaire fait par Edward Waring en 1770 dont John Wilson avait noté le résultat. John Wilson indique à Waring qu'il ne sait pas démontrer ce résultat, Waring ne trouve pas non plus de preuve. Pourtant la première démonstration connue provient de Leibniz, qui ne juge pas utile de la publier, et Euler en avait publié une preuve.Les nombres amiables ont joué un grand rôle dans les mathématiques islamiques. Au XIIIe siècle, le mathématicien perse Al-Farisi donna une nouvelle démonstration du théorème de Thabit ibn Qurra, introduisant de nouvelles idées concernant la décomposition et les méthodes combinatoires. Il donna aussi la paire de nombre amiables 17 296, 18 416 qui ont été attribués à Euler, mais nous savons que ceux-ci étaient connus plus tôt que Al-Farisi, peut-être même par Thabit ibn Qurra lui-même. Au XVIIe siècle, Muhammad Baqir Yazdi donna la paire de nombres amiables 9 363 584 et 9 437 056 toujours bien avant avant la contribution d'Euler.
Début de la théorie des nombres en Europe
La théorie des nombres en Europe commence aux XVIe et XVIIe siècles par les travaux de Viète, Bachet de Méziriac et surtout Fermat. Au XVIIIe siècle, Euler et Lagrange contribuèrent à la théorie, vers la fin du siècle, le sujet commence à prendre une forme scientifique à travers les grands travaux de Legendre (1798) et Gauss (1801). Avec ce dernier et son ouvrage, les Disquisitiones arithmeticae (1801), on peut dire que la théorie moderne des nombres commence.
Tchebychev (1850) donna des limites très utilisées pour les nombres premiers entre deux nombres donnés. Riemann (1859) conjectura que la limite de la densité des nombres premiers n'excède pas une fonction donnée (le théorème des nombres premiers), introduisit l'analyse complexe dans la théorie de la fonction ζ de Riemann, et en déduisit la formule des nombres premiers à partir de ses zéros.
L'arithmétique modulaire a réellement débuté avec les Disquisitiones arithmeticae de Gauss. Il introduisit le symbolisme suivant :
et explora la plus grande partie de ce domaine. Il généralise la théorie à d'autres anneaux de celui des entiers relatifs et découvre le premier ensemble d'entiers algébriques : les entiers de Gauss. Tchebychev publia en 1847 un travail en russe sur le sujet, et en France Serret le popularisa.
A côté du travail résumé précédemment, Legendre établit les premiers cas d'application loi de réciprocité quadratique. Cette loi, découverte par induction et énoncée par Euler, fut prouvée en premier par Legendre dans sa Théorie des Nombres (1798) pour des cas exceptionnels. Indépendamment d'Euler et Legendre, Gauss découvrit la loi vers 1795, et fut le premier à en donner une preuve générale. Au sujet contribuèrent aussi : Cauchy ; Dirichlet son Vorlesungen über Zahlentheorie est un classique ; Jacobi, qui introduisit le symbole de Jacobi ; Liouville, Zeller (?), Eisenstein, Kummer, et Kronecker. La théorie s'étendit pour inclure la réciprocité biquadratique et cubique, (Gauss, Jacobi qui fut le premier à prouver la loi de réciprocité cubique, et Kummer).
On doit aussi à Gauss la représentation des nombres par des formes quadratiques binaires. Cauchy, Poinsot (1845), Lebesgue (?) (1859, 1868), et notablement Hermite ont contribué à ce sujet. Dans la théorie des formes ternaires, Eisenstein a été un chef de file, et grâce à lui et aussi à H. J. S. Smith, on doit une avancée remarquable dans la théorie des formes en général. Smith donna une classification complète des formes quadratiques ternaires, et étendit les recherches de Gauss concernant les formes quadratiques réelles vers les formes complexes. Les recherches concernant la représentation des nombres par la somme de 4, 5, 6, 7, 8 carrés furent approfondies par Eisenstein et la théorie fut complétée par Smith.
Dans l'histoire de la théorie des nombres, le dernier théorème de Fermat joue un rôle à part, en raison des efforts considérables, étalés sur plus de trois cents ans, des mathématiciens du monde entier pour en apporter la preuve (ou la négation). Ce théorème affirme que pour n > 2, il n'existe pas d'entiers non nuls x, y et z vérifiant :
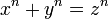 .
.
Pierre de Fermat lui-même en apporta la preuve dans le cas particulier n = 4. Euler, en 1753, le démontra presque pour n = 3, introduisant dans sa preuve les nombres imaginaires. En 1825, Dirichlet et Legendre démontrent le cas n = 5, en utilisant une avancée décisive de la française Sophie Germain (cf Démonstrations du dernier théorème de Fermat). Lamé résout le cas n = 7 en 1839. Ces différents cas sont résolus à l'aide de structure d'anneaux euclidien de la même nature que les entiers de Gauss, ce sont les anneau d'entiers d'Eisenstein et d'entiers de Dirichlet. Kummer en 1847 prouve le théorème lorsque l'exposant n est un nombre premier régulier, et ouvre la théorie de idéaux. À la fin du XIXe et au début du XXe siècle, les mathématiciens délaissent le grand théorème de Fermat pour se consacrer aux fondements des mathématiques. En 1955, les japonais Taniyama et Shimura émettent l'hypothèse d'un lien profond entre les fonctions elliptiques et les formes modulaires, deux domaines a priori très éloignés des mathématiques. Mais la conjecture de Shimura-Taniyama-Weil, si elle est vraie, a pour conséquence le grand théorème de Fermat. C'est Andrew Wiles qui prouvera cette conjecture en 1994 avec l'aide de Richard Taylor, et apportera une réponse définitive au célèbre problème.
Parmi les derniers auteurs français se trouvent Borel, Poincaré (leurs mémoires sont nombreux et de grande valeur), Tannery, et Stieltjes. Parmi les plus grands contributeurs en Allemagne se trouvent Kronecker, Kummer, Schering, Bachmann, et Dedekind. En Autriche, le travail de Stolz Vorlesungen über allgemeine Arithmetik (1885-1886), et en Angleterre George B. Mathews, sa 'Théorie des nombres (Part I, 1892)' est l'un des plus érudits des travaux généraux. Genocchi, Sylvester, et Glaisher ont aussi participé à la théorie.
Citation
La mathématique est la reine des sciences et la théorie des nombres est la reine des mathématiques. Gauss
Bibliographie
(en) Jürgen Neukirch, Alexander Schmidt, Kay Wingberg Cohomology of number fields [détail des éditions]
Références
- ↑ Introduction à l'ouvrage Cohomology of number fields. « Die Zahlentheorie nimmt unter den mathematishen Disziplinen eine ähnlich idealisierte Stellung ein wie die Mathematik selbst unter den anderen Wissenschaften. »
Voir aussi
Liens externes
- Portail des mathématiques
Catégorie : Théorie des nombres
Wikimedia Foundation. 2010.