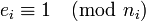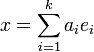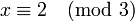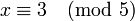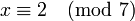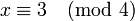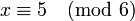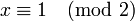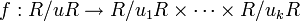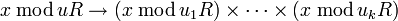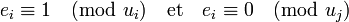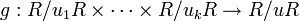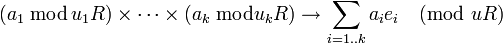- Theoreme des restes chinois
-
Théorème des restes chinois
Le théorème des restes chinois est un résultat d'arithmétique modulaire traitant de résolution de systèmes de congruences. Ce résultat établi initialement sur Z/nZ se généralise en théorie des anneaux. Ce théorème est utilisé en théorie des nombres.
Sommaire
Fragments d'histoire
La forme originale du théorème, contenue dans un livre du mathématicien chinois Qin Jiushao publié en 1247, est un résultat concernant les systèmes de congruences (voir arithmétique modulaire). Mais on trouve trace d'un problème analogue dans le livre de Sun Zi, le Sunzi suanjing datant du IIIe siècle :
- Combien l'armée de Han Xing comporte-t-elle de soldats si, rangés par 3 colonnes, il reste deux soldats, rangés par 5 colonnes, il reste trois soldats et, rangés par 7 colonnes, il reste deux soldats ?
On peut penser que les Chinois, férus de calculs astronomiques puissent être intéressés par des concordances de calendrier et qu'ils aient été amenés très tôt à s'intéresser à des questions du type :
- Dans combien de jours la pleine lune tombera-t-elle au solstice d'hiver ?
Si la question se pose alors qu'il reste 6 jours avant le solstice d'hiver et 3 jours avant la pleine lune, la question se traduit par:
- Existe-t-il un entier x tel que le reste de la division de x par 365 donne 6 et le reste de la division de x par 28 donne 3 ?
La résolution proposée par Sun Zi pour le problème des soldats est la suivante :
- Multiplie le reste de la division par 3, c’est-à-dire 2, par 70, ajoute lui le produit du reste de la division par 5, c’est-à-dire 3, avec 21 puis ajoute le produit du reste de la division par 7, c'est à dire 2 par 15. Tant que le nombre est plus grand que 105, retire 105.
Mais la solution n'explique qu'imparfaitement la méthode utilisée.
Enfin, il serait dommage de ne pas présenter ce problème concernant des pirates et un trésor, très fréquemment cité pour illustrer le théorème des restes chinois :
- Une bande de 17 pirates possède un trésor constitué de pièces d'or d'égale valeur. Ils projettent de se les partager également, et de donner le reste au cuisinier chinois. Celui-ci recevrait alors 3 pièces. Mais les pirates se querellent, et six d'entre eux sont tués. Un nouveau partage donnerait au cuisinier 4 pièces. Dans un naufrage ultérieur, seuls le trésor, six pirates et le cuisinier sont sauvés, et le partage donnerait alors 5 pièces d'or à ce dernier. Quelle est la fortune minimale que peut espérer le cuisinier s'il décide d'empoisonner le reste des pirates ?
L'arithmétique modulaire a rendu ce type de problème plus facile à résoudre.
Système de congruences d'entiers
Théorème
Soient n1, ..., nk des entiers deux à deux premiers entre eux (ce qui veut dire pgcd (ni , nj) = 1 lorsque i ≠ j). Alors pour tous entiers a1, ..., ak, il existe un entier x, unique modulo
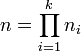 et tel que
et tel que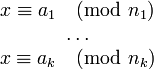
Une solution x peut être trouvée comme suit:
Pour chaque i, les entiers
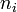 et
et 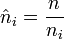 sont premiers entre eux, et d'après le théorème de Bachet-Bézout, on peut trouver des entiers
sont premiers entre eux, et d'après le théorème de Bachet-Bézout, on peut trouver des entiers 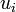 et
et 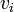 tels que
tels que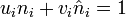 . Si on pose
. Si on pose 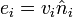 , alors nous avons
, alors nous avonset
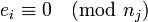 pour j ≠ i.
pour j ≠ i.
Une solution de ce système de congruences est par conséquent
Plus généralement, toutes les solutions x de ce système sont congrues modulo le produit n
Exemple
Le problème des soldats se réduit à
on obtient alors
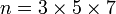
- n1 = 3 et
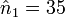 , or
, or  donc e1 = 70
donc e1 = 70 - n2 = 5 et
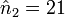 , or
, or 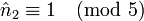 donc e2 = 21
donc e2 = 21 - n3 = 7 et
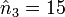 , or
, or 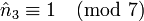 donc e3 = 15
donc e3 = 15
une solution pour x est alors
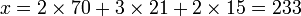
et les solutions sont tous les entiers congrus à 233 modulo 105, c'est-à-dire à 23 modulo 105.
Généralisation à des nombres non premiers entre eux
Quelquefois, les systèmes de congruences peuvent être résolus même si les
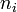 ne sont pas premiers entre eux deux à deux. Le critère précis est le suivant : une solution x existe si et seulement si
ne sont pas premiers entre eux deux à deux. Le critère précis est le suivant : une solution x existe si et seulement si 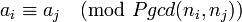 pour tous i et j. Toutes les solutions x sont congrues modulo le PPCM des ni .
pour tous i et j. Toutes les solutions x sont congrues modulo le PPCM des ni .Exemple : résoudre le système
équivaut à résoudre le système
équivaut au système
- n1 = 4 et
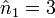 , or
, or  donc e1 = 9
donc e1 = 9 - n2 = 3 et
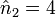 , or
, or 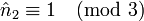 donc e2 = 4
donc e2 = 4
Une solution est donc
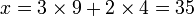 ou tout autre nombre congru à 11 modulo 12
ou tout autre nombre congru à 11 modulo 12La méthode des substitutions successives peut souvent fournir les solutions des systèmes de congruences, même lorsque les modules ne sont pas premiers entre eux deux à deux.
Interprétation mécanique
La résolution du système suivant :
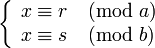
d'inconnue x passe par le calcul du PPCM de a et b.
Ce problème mathématique est une modélisation d'un problème sur des engrenages: une roue dentée comportant a dents s'engrène dans une tringle horizontale. Combien de dents doivent passer pour que sa r-ième dent vienne en coïncidence avec la s-ième dent d'une autre roue dentée comportant elle b dents ?
Le PPCM des deux nombres a et b est ce qui permet de comprendre le comportement périodique de ce système : c'est le nombre de dents séparant deux contacts de même congruence. On peut donc trouver la solution , s'il y en a une, dans l'intervalle [1,PPCM(a,b)]. Il y a une solution si PGCD(a , b) divise r - s.

On peut comprendre simplement pourquoi le calcul sur des roues dentées fait intervenir de l'arithmétique modulaire, en remarquant que l'ensemble des dents d'une roue en comptant n peut être paramétré par l'ensemble des racines nèmes de l'unité, qui a une structure de groupe naturellement isomorphe à celle de Z/nZ.
Résultat pour les anneaux
Dans les anneaux
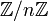 Article détaillé : Anneau Z/nZ.
Article détaillé : Anneau Z/nZ.Le théorème chinois a également une version plus abstraite : si n1, ..., nk sont deux à deux premiers entre eux alors, en notant n le produit de ni, l'application
![\begin{matrix}
\phi:&\mathbb{Z}/n\mathbb{Z} &\longrightarrow& \mathbb{Z}/n_1\mathbb{Z}\times\cdots\times\mathbb{Z}/n_k\mathbb{Z}\\
&\alpha &\longmapsto& (\alpha[n_1],\dots,\alpha[n_k])
\end{matrix}](/pictures/frwiki/99/cced46326dfd34fa81af947bea678e5c.png)
est un isomorphisme d'anneau.
Pour le montrer on remarque d'abord que les deux ensembles
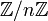 et
et 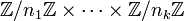 ont le même nombre d'éléments. Comme
ont le même nombre d'éléments. Comme 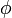 est un morphisme d'anneau, il suffit donc de voir qu'il est injectif pour en déduire que c'est un isomorphisme. Pour voir cela il suffit de montrer que son noyau est réduit à 0 : si α = 0[ni] pour
est un morphisme d'anneau, il suffit donc de voir qu'il est injectif pour en déduire que c'est un isomorphisme. Pour voir cela il suffit de montrer que son noyau est réduit à 0 : si α = 0[ni] pour 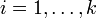 , c’est-à-dire si α est un multiple de chaque ni, alors α = 0[n], c’est-à-dire α est un multiple du produit
, c’est-à-dire si α est un multiple de chaque ni, alors α = 0[n], c’est-à-dire α est un multiple du produit 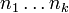 . Ceci résulte de l'hypothèse que les ni sont premiers entre eux deux à deux.
. Ceci résulte de l'hypothèse que les ni sont premiers entre eux deux à deux.
Dans le cas où les ni ne sont pas premiers entre eux, n est leur ppcm et le morphisme ci-dessus n'est qu'injectif. Il existe une solution au problème initial si et seulement si les données sont dans l'image, c'est-à-dire que le pgcd de ni et nj divise αi − αj pour tout couple i,j.Dans un anneau principal
Pour un anneau principal R, le théorème des restes chinois prend la forme suivante : Si u1, ..., uk sont les éléments de R qui sont premiers entre eux deux à deux, et u désigne le produit u1...uk, alors l'anneau R/uR et l'anneau produit R/u1R x ... x R/ukR sont isomorphes par l'isomorphisme
tel que
L'isomorphisme inverse peut être construit comme ceci. Pour chaque i, les éléments ui et u/ui sont premiers entre eux, et par conséquent, il existe des éléments r et s dans R avec
- rui + su / ui = 1
Fixons ei = s u/ui. On a :
pour j ≠ i.
Alors l'inverse est la transformation
telle que
Résultat pour les anneaux généraux
Une des formes les plus générales du théorème des restes chinois peut être formulée en termes d'anneau et d'idéal (à gauche ou à droite). Si R est un anneau et I1, ..., Ik des idéaux de R qui sont deux à deux premiers entre eux (ce qui signife que Ii + Ij = R lorsque i ≠ j), alors l'idéal produit I de ces idéaux est égal à leur intersection, et l'anneau quotient R/I est isomorphe à l'anneau produit R/I1 x R/I2 x ... x R/Ik via l'isomorphisme de R / I dans
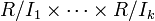 qui à
qui à 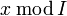 associe
associe 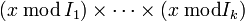 .
.Exemple des polynômes
Un cas fréquent illustrant le paragraphe précédent est donné par l'anneau
![\mathbb K[X]](/pictures/frwiki/49/11cf18672fa8c102e5d2ec8bdfe203c8.png) des polynômes. Si x0, x1, ..., xn sont n+1 éléments de
des polynômes. Si x0, x1, ..., xn sont n+1 éléments de 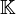 distincts deux à deux, alors on peut prendre Ui = X - xi . Les polynômes Ui sont premiers entre eux deux à deux, et le théorème des restes chinois s'applique. On prend pour Ei les polynômes interpolateurs de Lagrange, définis par :
distincts deux à deux, alors on peut prendre Ui = X - xi . Les polynômes Ui sont premiers entre eux deux à deux, et le théorème des restes chinois s'applique. On prend pour Ei les polynômes interpolateurs de Lagrange, définis par : 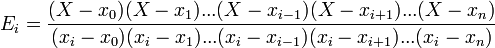 .
.Pour j différent de i, Ei est divisible par Uj , de sorte que Ei ≡ 0 modulo Uj . Par ailleurs, modulo Ui , X ≡ xi , de sorte que Ei ≡ 1 modulo Ui .
Dire qu'un polynôme P est tel que P(xi) = yi pour tout i, est équivalent à dire que P ≡ yi modulo Ui . Un tel polynôme P est donné par
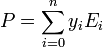 , ce qu'on peut vérifier par un calcul direct.
, ce qu'on peut vérifier par un calcul direct.Utilisations
Le théorème des restes chinois est utilisé en particulier dans l'algorithme RSA en cryptographie.
Il permet de représenter de grands nombres entiers comme n-uplets de restes de divisions euclidiennes. Sous cette forme, des opérations comme l'addition ou la multiplication peuvent se faire en parallèle en temps constant (pas de propagation de retenue). Par contre, la comparaison ou la division ne sont pas triviales.
Liens externes
- Portail des mathématiques
Catégories : Arithmétique modulaire | Algèbre | Théorème de mathématiques
Wikimedia Foundation. 2010.