- Theorie de Galois
-
Théorie de Galois
En mathématiques et plus précisément en algèbre, la théorie de Galois est l'étude des extensions de corps commutatifs, par le biais d'une correspondance avec des groupes de transformations sur ces extensions, les groupes de Galois. Cette méthode féconde, qui constitue l'exemple historique, a essaimé dans bien d'autres branches des mathématiques, avec par exemple la théorie de Galois différentielle, ou la théorie de Galois des revêtements.
Cette théorie est née de l'étude par Évariste Galois des équations algébriques. L'analyse de permutations des racines permet d'expliciter une condition nécessaire et suffisante de résolubilité par radicaux. Ce résultat est connu sous le nom de théorème d'Abel-Ruffini.
Les outils essentiels de la théorie sont les extensions de corps et les groupes de Galois.
Les applications sont très variées. Elles s'étendent de la résolution de vieilles conjectures comme la détermination des polygones constructibles à la règle et au compas démontrée par le théorème de Gauss-Wantzel à la géométrie algébrique à travers, par exemple, le théorème des zéros de Hilbert.
Sommaire
Histoire
Genèse
La théorie de Galois voit ses origines dans l'étude des équations algébriques. Elle se ramène à l'analyse des équations polynomiales. Une approche par des changements de variables et des substitutions a permis à des mathématiciens comme Al-Khwarizmi[1] (783 850), Tartaglia (1499 1557), Cardano[2] (1501 1576) ou Ferrari (1522 1565) de résoudre tous les cas jusqu'au degré quatre. Cette approche ne permet pas d'aller plus loin et deux siècles seront nécessaires pour apporter de nouvelles idées.
Gauss et les polynômes cyclotomiques
Paragraphe détaillé : Histoire des polynômes cyclotomiques
Gauss (1777 1855) utilise les polynômes cyclotomiques[3] pour apporter une contribution à un problème ouvert depuis l'antiquité: celui de la construction à la règle et au compas de polygones réguliers. Il construit en particulier l'heptadécagone, polygone régulier à 17 cotés. Son approche, typiquement galoisienne bien avant la découverte de la théorie, lui vaut le surnom de prince des mathématiciens.
Son travail est complété par Wantzel[4] (1814 1848), qui donne une condition nécessaire et suffisante de constructibilité des polygones réguliers et démontre l'impossibilité de la trisection de l'angle et de la duplication du cube.
Théorème d'Abel-Ruffini
Paragraphe détaillé : Histoire du théorème d'Abel-Ruffini
Dans le cas général, l'équation quintique n'admet pas de solution par radicaux. C'est la raison pour laquelle une démarche à l'aide de substitutions et changements de variables devient stérile. Lagrange[5] (1736 1813) et Vandermonde[6] (1735 1796) utilisent la notion de permutation à la fin du XVIIIe siècle et pressentent l'importance de cet outil dans le cadre de l'équation polynomiale.
Ruffini[7] (1765 1822) est le premier à prévoir l'impossibilité de la solution générale et que la compréhension du phénomène réside dans l'étude des permutations des racines. Sa démonstration reste néanmoins peu rigoureuse et partielle. Le mathématicien norvégien Abel (1802 1829) publie une démonstration[8] en 1824 qui finit par convaincre la communauté scientifique. Elle ne propose pas à l'époque de condition nécessaire et suffisante de résolubilité.
Évariste Galois
Article détaillé : Histoire des groupes de Galois.En étudiant le problème de l'équation algébrique, Galois (1811 1832) met en évidence les premiers éléments de la théorie qui porte maintenant son nom. Ses écrits sont perdus ou tombent dans l'oubli. Un mémoire[9] est finalement retrouvé par Liouville (1809 1882) qui le présente à l'Académie des sciences en 1843. Les travaux de Galois accèdent alors in extremis à la postérité.
Galois, pour la première fois dans l'histoire des mathématiques, met en évidence une structure abstraite qu'il appelle groupe. À la différence de ses prédécesseurs, il n'étudie pas une incarnation particulière comme les permutations de Lagrange ou les groupes cycliques de Gauss, mais une structure générale définie par un ensemble et une loi.
Cette démarche, particulièrement novatrice, est à l'origine de l'algèbre moderne. Liouville en parle dans les termes suivants : « Cette méthode, vraiment digne de l'attention des géomètres, suffirait seule pour assurer à notre compatriote un rang dans le petit nombre des savants qui ont mérité le titre d'inventeur. »[10]
Structures algébriques
L'apport majeur de Galois, c'est-à-dire l'utilisation d'une structure algébrique comme outil fondamental, est rapidement compris par la communauté mathématique. Cauchy (1789 1855) publie vingt-cinq articles sur les groupes dont un sur son célèbre théorème[11]. Cayley (1821 1895) donne la première définition abstraite d'un groupe[12]. Enfin, Jordan (1838 1922) diffuse largement les idées de Galois. Son livre[13] de 1870 présente les travaux de Galois comme une théorie générale sur des groupes, dont le théorème sur la résolution des équations n'est qu'une application. En France, la théorie de Galois est identifiée à celle des groupes à cette époque.
D'autres structures sont mises en évidence, particulièrement en Allemagne. Indépendamment des travaux de Galois, Kummer (1810 1893) étudie[14] des anneaux et découvre l'ancêtre de la notion d'idéal. Kronecker (1823 1891) et Dedekind (1831 1916) développent les prémisses de la théorie des anneaux et des corps[15]. Kronecker établit le pont entre les écoles française et allemande. Il donne la définition moderne de groupe de Galois à partir d'automorphismes de corps.
A la fin du XIXe siècle, Weber (1842 1913) réalise une synthèse[16] des différents travaux. La théorie de Galois est alors pour la première fois identifiée avec celle des corps commutatifs.
Théories de Galois
 Icosaèdre
Icosaèdre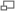
Un nouvel axe d'analyse enrichit la théorie de Galois. En 1872 Klein (1849 1925) se fixe comme objectif de classifier les différentes géométries de l'époque. Il dégage, dans son célèbre programme d'Erlangen, le principe général qu'une géométrie est définie par un espace et un groupe opérant sur cet espace, appelé groupe des isométries. Un pont est ainsi établi entre la théorie des groupes et la géométrie. Ces premiers groupes correspondent à des groupes de Lie et n'appartiennent pas directement à ceux de la théorie de Galois.
En 1877 Klein remarque[17] que le groupe des isométries laissant invariant l'icosaèdre est isomorphe au groupe de Galois d'une équation quintique. La théorie de Galois s'étend à la géométrie algébrique. Les groupes de Galois prennent alors la forme de revêtements aussi appelés revêtement de Galois. David Hilbert (1862 1943) étudie les corps de nombres quadratiques et apporte une contribution majeure à la théorie en démontrant[18] son célèbre théorème des zéros. Ce théorème possède aussi une interprétation géométrique sur les variétés algébriques. La théorie est maintenant enrichie d'une nouvelle branche: la théorie de Galois géométrique. Elle s'avère particulièrement féconde.
Les travaux de Hilbert ouvrent d'autres branches de la théorie de Galois. Le théorème des zéros permet l'étude des premiers groupes de Galois d'ordre infini. Son théorème d'irréductibilité ouvre la problématique inverse. Elle s'énonce de la manière suivante : si G est un groupe alors est-il le groupe de Galois d'une extension?
Enfin les travaux de Picard (1856 1941) et Vessiot (1865 1952) ouvrent une autre voie pour l'étude des groupes de Galois d'ordre infini, la théorie de Galois différentielle.
Apports du XXe siècle
Les travaux de Hilbert ont ouvert l'étude des cas où le groupe de Galois est d'ordre infini et commutatif. Ce vaste sujet prend le nom de théorie des corps de classes. Elle est maintenant achevée et est souvent considérée comme un des plus beaux succès des mathématiques du siècle.
La formalisation définitive[19] de la théorie de Galois est donnée par Artin. L'adjonction de l'algèbre linéaire permet une exposition plus claire et concise. La théorie utilise maintenant toutes les grandes structures de l'algèbre, les groupes, les anneaux, les corps et les espaces vectoriels. Elle dispose maintenant de ramifications importantes en géométrie algébrique.
Elle est la base d'une quantité majeure des grandes réalisations mathématiques du XXe siècle. L'alliance de la géométrie et de l'algèbre est presque systématiquement utilisée. On peut citer par exemple les travaux des mathématiciens Jean-Pierre Serre (Médaille Fields 1954) et Grothendieck (Médaille Fields 1966) avec une refonte de la géométrie algébrique, Faltings (Médaille Fields 1986) pour ses travaux sur les modules de Galois démontrant le théorème de Mordell ou Laurent Lafforgue (Médaille Fields 2002) sur le Programme de Langlands, une généralisation de la théorie des corps de classes.
Exemples
Petit théorème de Fermat
Article détaillé : Théorie algébrique des nombres.Le petit théorème de Fermat nous indique que si a est un entier et p un nombre premier alors:
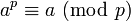
Il est possible de démontrer ce théorème en remarquant que Fp le quotient de l'ensemble des nombres entiers par son idéal engendré par p est un corps, car p est un nombre premier. (Fp*, .) est un groupe fini de cardinal p -1. Le théorème de Lagrange assure que tout élément de ce groupe à la puissance p -1 est égal à l'unité, ce qui démontre le théorème.
Conclusion : Ce cas est particulièrement aisé car la structure du corps est simple. Il illustre néanmoins le fait qu'une structure de corps est un outil utile en théorie algébrique des nombres. D'autres théorèmes d'arithmétique modulaire comme la loi de réciprocité quadratique demandent une compréhension beaucoup plus profonde de la structure des corps. C'est la raison pour laquelle la démonstration ne put être trouvée malgré leurs efforts par Euler (1707 1783) ou Lagrange et qu'il fallut attendre Gauss et ses polynômes cyclotomiques pour conclure.
Duplication du cube
Articles détaillés : Extension quadratique et Tour d'extension quadratique.Soit L l'ensemble des éléments de la forme a + b.√2 où a et b sont des rationnels.
Montrons que L est un corps : L est clairement stable pour l'addition et le passage à l'opposé, et est donc un groupe additif. Il est stable pour la multiplication et le passage à l'inverse des éléments non nuls, en effet:
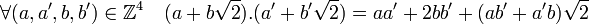
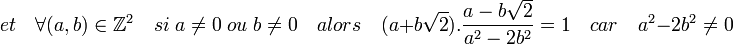
Ces deux dernières propositions montrent que L est un sous-corps des nombres réels. L est aussi un espace vectoriel de dimension deux sur les nombres rationnels, car il possède pour base 1 et √2. Un tel corps s'appelle une extension quadratique.
Montrons que L ne contient pas la racine cubique de deux : Soit l un élément de L, alors de l 2 est une combinaison linéaire à coefficients rationnels de 1 et √2 car ces deux éléments forment une base et l 2 est un élément de L. il existe donc deux rationnels α et β tel que l'égalité suivante est vraie:
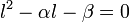
Et pour tout élément l de L il existe un polynôme de degré inférieur ou égal à deux ayant pour racine l. Or, le plus petit degré du polynôme non nul à coefficients rationnels qui annule la racine cubique de deux est trois, et la proposition est démontrée.
Conclusion : Wantzel a démontré que les nombres constructibles à la règle et au compas sont soit dans une extension quadratique, soit dans une extension quadratique dont les coefficients sont pris dans une extension quadratique et ainsi de suite. On parle alors de tour d'extension quadratique. Il est possible de démontrer par un raisonnement analogue à celui présenté ici que la racine cubique de deux n'est pas élément d'une tour d'extension quadratique. Voilà pourquoi la duplication du cube est impossible. Le choix judicieux de corps particuliers est la clé de la résolution de cette antique conjecture.
Équation cubique
Article détaillé : Théorème d'Abel-Ruffini.
Considérons un exemple d'équation du troisième degré :
![P[X]=0 \quad avec \quad P[X]=X^3-3X+1\;](/pictures/frwiki/102/ff8d27380fe47a3187dffab0b36de1a4.png)
Détermination d'un élément du groupe de Galois : Le polynôme P[X] est un polynôme irréductible à coefficients rationnels. La théorie de Galois nous indique qu'il existe un corps L qui est une extension des rationnels contenant toutes les racines de P[X]. Cette extension est de dimension six. De plus, il existe un sous-corps K de L tel que L est de dimension trois sur K et j la première racine cubique de l'unité est élément de K. Le groupe de Galois de L sur K est l'ensemble des automorphismes de corps de L laissant invariant tout élément de K. La théorie de Galois nous indique que ce groupe a trois éléments, soit g un élément du groupe différent de l'identité.
Diagonalisation de g : Le théorème de Lagrange nous assure que g3 est égal à l'identité. Si l est un élément non nul de L, alors l, g(l) et g2(l) forment une base de L sur K. Considérant g comme opérateur linéaire, son polynôme caractéristique est X3 - 1 et ses valeurs propres sont 1, j et j2. Il existe une base (u, v, w) de L sur K constituée de vecteurs propres, car le nombre de valeurs propres est égal à la dimension de L sur K. On a donc g(u)=j·u, g(v)=j2·v et g(w)=w. De plus, 1 + j + j2 = 0.
Détermination de l'image des racines par g : Soit x1, une racine de P[X]. L'image d'une racine par g est une racine, en effet:

On en déduit que x1, g(x1) et g2(x1) sont les trois racines de P. On peut repésenter x1 comme somme de vecteurs propres de g: x1 = u + v + w (léger abus de notation: w sera en l'occurrence 0, ne formant plus une base comme ci-dessus). Les trois égalités suivantes sont alors vérifiées:
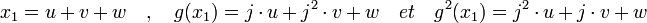
Calcul des valeurs des racines : Il suffit d'utiliser les relations entre coefficients et racines pour montrer que :
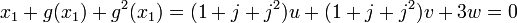 , donc
, donc 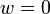
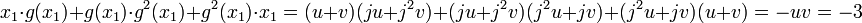 , donc
, donc 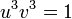
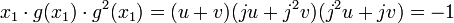 , donc
, donc 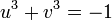
On en déduit que u 3 et v 3 vérifient l'équation X2 + X + 1 = 0. Ce qui permet de conclure que x1 est égal à 2 cos(2π/9), 2 cos(8π/9) ou 2 cos(14π/9).
Conclusion : Le groupe de Galois, permet la résolution de l'équation cubique par une diagonalisation d'un endomorphisme. La méthode est généralisable si et seulement si le groupe de Galois possède de bonnes propriétés, en fait s'il est résoluble.
Synthèse
Ces exemples ont un point commun, ce sont les propriétés des structures algébriques qui permettent de trouver les solutions. Pour le premier exemple, la propriété démontrée par Lagrange sur les groupes (et donc les groupes multiplicatifs des corps) finis permet de conclure. Dans le deuxième exemple, ce sont les propriétés associées sur la dimension d'un l'espace vectoriel qui sont utilisées. Dans le troisième cas, sont utilisés les propriétés des corps et de leurs extensions, des groupes avec le théorème de Lagrange et celle des espaces vectoriels avec les propriétés de réduction d'endomorphisme dans le cas où le polynôme minimal est scindé.
La théorie de Galois offre une richesse dans les structures algébriques permettant de résoudre nombre de cas très différents et dans des domaines éloignés.
Applications
Théorie algébrique des nombres
La théorie algébrique des nombres est l'étude des nombres racines d'un polynôme à coefficients entiers, appelés nombres algébriques.
La théorie de Galois est ici essentielle car elle offre la structure la plus adéquate d'analyse, à savoir l'extension finie la plus petite contenant les nombres étudiés. Un sous-ensemble joue un rôle particulier : celui des entiers algébriques, ils correspondent à la généralisation des entiers dans l'extension. L'étude de cet ensemble ajoute à la théorie de Galois de nombreuses propriétés issues de la théorie des anneaux. Les entiers algébriques jouent un rôle important pour la résolution d'équations d'arithmétique modulaire ou diophantiennes.
On peut citer comme application de la théorie de Galois à ce domaine, le théorème de Gauss-Wantzel qui détermine tous les polygones réguliers constructibles à la règle et au compas. La Théorie de Kummer s'applique aux équations diophantiennes et permet de valider le grand théorème de Fermat pour presque tous les entiers inférieurs à cent. Enfin, dans le cadre de l'arithmétique modulaire, la loi de réciprocité d'Artin généralise la loi de réciprocité quadratique de Gauss et résout le neuvième problème de Hilbert.
Cryptographie
 La machine Lorenz utilisée par les Allemands durant la Seconde Guerre mondiale
La machine Lorenz utilisée par les Allemands durant la Seconde Guerre mondiale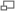
La cryptographie est la discipline qui s'attache à protéger un message. Le cadre théorique maintenant le plus utilisé consiste à définir un algorithme qui, associé à une clef permet de créer un nouveau message dit cryptogramme signifiant qu'il est chiffré. Le message chiffré est simple à déchiffrer, c'est-à-dire simple à transformer en message d'origine avec une clef et difficile sans celle-ci pour la personne qui s'efforce alors de le décrypter.
Dans une partie des théories modernes de cryptographie, les lettres du message sont choisies dans un corps fini. Le cadre est donc celui de la théorie de Galois.
Il est naturel que les outils associés soient ceux de la théorie. L'arithmétique modulaire (cf par exemple l'algorithme RSA) est très largement employée. Si les techniques simples reposent sur des résultats élémentaires comme le théorème de Bézout, le théorème des restes chinois ou l'exponentiation modulaire, les développements actuels utilisent des outils plus subtils comme les courbes elliptiques (cf une clé privée inviolable ?).
Théorie des équations algébriques
La problématique de la théorie des équations algébriques est celle qui donna naissance à la théorie de Galois. Elle complète le théorème d'Abel-Ruffini en proposant une condition nécessaire et suffisante pour l'existence d'une expression par radicaux des racines d'un polynôme.
Elle permet néanmoins d'aller plus loin. Le théorème de Kronecker-Weber explicite précisément la structure des extensions rationnelles associées aux polynômes ayant des racines s'exprimant par radicaux. Il devient alors possible de résoudre explicitement toutes les équations de cette nature.
Elle possède pour champs d'application tous les corps, offrant un outil puissant à l'arithmétique modulaire. Beaucoup de lois de réciprocité, de même nature que celle démontrée par Gauss dans le cas quadratique sont ainsi démontrables grâce à la théorie de Galois.
Abel puis Hermite (1822 1902) ont travaillé sur une autre approche : les fonctions elliptiques. Elles permettent, par exemple, d'exprimer les racines de toute équation polynomiale. La théorie géométrique de Galois intégre cette notion à travers les courbes elliptiques. Le grand théorème de Fermat a été démontré à l'aide de méthodes de cette nature.
Il existe une théorie de Galois un peu particulière traitant des équations différentielles polynomiales. Cette théorie prend le nom de théorie de Galois différentielle. Elle étudie une famille particulière de corps appelée extension différentielle. Ces corps possèdent des groupes de Galois. La résolution d'une équation algébrique correspond aussi à l'analyse du groupe associé et permet la résolution d'une équation différentielle.
Géométrie algébrique
Les structures utilisées
Corps commutatifs
Articles détaillés : corps (mathématiques) et extension de corps.Le corps commutatif est l'objet de la théorie de Galois. C'est donc naturellement la structure centrale de la théorie.
La technique la plus importante de construction correspond à l'extension, c'est-à-dire à un corps qui contient le corps d'origine. À partir d'un corps de base, souvent le plus petit, celui engendré par l'unité, qui est un corps cyclique (construit à partir d'un groupe cyclique d'ordre un nombre premier) ou celui des rationnels une nouvelle structure est créée.
Cette méthode permet la création d'une zoologie décrivant les différentes propriétés de la structure. Un corps peut ainsi être par exemple algébrique, simple, parfait, quadratique, séparable, cyclotomique ou algébriquement clos.
Il existe des théorèmes importants, comme celui de l'élément primitif ou celui de Wedderburn qui assurent que tout corps fini est commutatif.
Espace vectoriel
Article détaillé : Extension finie.Une extension possède une structure d'espace vectoriel sur son corps de base. Cette structure est importante à deux titres:
Elle permet de classifier l'étude des différents corps, ceux de dimension finie dit encore extension finie et les autres. De même qu'en algèbre linaire, le premier cas est infiniment plus simple que l'autre.
Elle est ensuite un outil qui permet la démonstration de nombreuses propriétés en adjoignant à la théorie les théorèmes d'algèbres linéaires. On peut citer par exemple le théorème de Gauss-Wantzel dont la démonstration se trouve dans le paragraphe applications des tours d'extension quadratique ou le théorème d'Abel-Ruffini qui utilise une diagonalisation d'endomorphisme.
Le cas de dimension infinie est largement plus complexe, il est partiellement traité dans la théorie des corps de classe.
Anneau
Article détaillé : Extension algébrique.Un outil important de la théorie est le polynôme formel. Et la structure d'anneau est celle de l'ensemble des polynômes. Il est utilisé par exemple pour construire des extensions. Une extension est ainsi souvent le quotient de l'anneau des polynômes par un idéal engendré par un polynôme irréductible.
Un polynôme joue un rôle particulier dans la théorie: le polynôme minimal qui est le polynôme unitaire de plus petit degré qui possède pour racine un élément donné. Ainsi, une extension est algébrique si tous les éléments possèdent un polynôme minimal, quadratique si le polynôme minimal de tout élément est de degré inférieur ou égal à deux, séparable si aucun polynôme minimal n'a de racine multiple, cyclotomique si l'extension est engendrée par une racine d'un polynôme cyclotomique. Un corps est parfait si toute extension est séparable.
La théorie algébrique des nombres utilise aussi souvent des sous-ensembles d'une extension ne disposant que d'une structure d'anneau, comme par exemple les entiers algébriques.
Groupe
Articles détaillés : Groupe de Galois et Théorème fondamental de la théorie de Galois.Cette structure est l'apport majeur du mathématicien portant le nom de la théorie.
Le groupe de Galois est le groupe des automorphismes d'une extension laissant invariant le corps de base. Sous certaines conditions relativement générales, le corps est entièrement caractérisé par son groupe de Galois. Une extension satisfaisant ces conditions est dite galoisienne. En particulier, si la structure d'espace vectoriel est de dimension finie, alors le groupe d'une extension abélienne a pour ordre la dimension du groupe.
Comme il est largement plus simple d'étudier un groupe fini qu'une structure de corps, l'analyse du groupe est une puissante méthode pour comprendre le corps. Le groupe de Galois est à l'origine de nombreux théorèmes. On peut citer le théorème fondamental de la théorie, le théorème d'Abel-Ruffini ou celui de Kronecker-Weber.
Topologie
Théories de Galois
Théorie classique
Le terme de classique est largement utilisé, même s'il ne possède pas de définition précise. On le trouve par exemple, sur la page de présentation d'un membre de l'Académie des sciences : Jean-Pierre Ramis. Il est aussi utilisé largement par Daniel Bertrand professeur à l'université de Paris VI.
Il désigne en général la théorie recouvrant les extensions algébriques finies et séparables. la théorie traite essentiellement des extensions normales et donc galoisiennes. Les résultats principaux sont le théorème de l'élément primitif et le théorème fondamental de la théorie de Galois. Ce cadre permet par exemple la démonstration du théorème d'Abel-Ruffini de Gauss-Wantzel ou de Kronecker-Weber, il est utilisé dans la classification des corps finis.
L'étendue de cette théorie couvre l'état de la science à l'époque de Weber c'est-à-dire la fin du XIXe siècle, même si maintenant elle est très généralement présenté avec le formalisme d'Artin. Cela correspond un peu au cas de la dimension finie pour l'algèbre linéaire.
Théorie de Galois infinie
La théorie de Galois classique traite le cas des extensions algébriques finies. Toutefois, elle ne s'avère pas assez puissante pour traiter aussi celui des extensions algébriques infinies. Pour cela une étude algébrique ne s'avère pas suffisante, il faut y ajouter l'utilisation de propriétés topologiques.
Une extension algébrique est dite galoisienne si elle est séparable et normale. Son groupe de Galois peut alors être défini comme dans le cas classique, mais on y ajoute une topologie qui en fait un groupe topologique compact. Dans le cas d'une extension finie, cette topologie est discrète, de sorte que la seule information contenue dans le groupe de Galois est de nature algébrique.
Dans ce cadre, il existe un analogue au théorème fondamental de la théorie de Galois, qui donne une correspondance entre les sous-groupes fermés du groupe de Galois et les extensions intermédiaires de corps.
Théorie géométrique
Théorie inverse
Il est en général difficile de déterminer le groupe de Galois d'une extension donnée. Cette remarque pose naturellement la problématique inverse: soit un groupe donné, quel est l'extension sur un corps donné qui possède ce groupe comme groupe de Galois? Cette question est celle à laquelle la théorie inverse cherche à répondre.
Dans le cas des groupes finis, un premier résultat montre que si n est un entier strictement positif alors il existe une extension du corps des rationnels ayant pour groupe de Galois le groupe symétrique d'ordre n. Par exemple, le corps de décomposition du polynôme rationnel Xn - X - 1 admet pour groupe de Galois le groupe symétrique d'ordre n. Le théorème de Cayley et le théorème fondamental de la théorie de Galois permet d'en déduire que, pour tout groupe fini G, il existe une extension d'un corps de nombres (c'est-à-dire une extension finie des nombres rationnels) ayant G pour groupe de Galois.
La théorie inverse cherche à répondre à trois questions :
-
- Soit un groupe G et un corps K, existe-t-il une extension de K ayant G pour groupe de Galois ?
- Soit un groupe fini G, existe-t-il une extension normale des rationnels ayant G pour groupe de Galois ?
- Soit un groupe fini G et un corps K, existe-t-il une extension normale de K ayant G pour groupe de Galois ?
Malgré d'importants progrès durant les trente dernières années du XXe siècle, en 2006 les trois questions restent très largement ouvertes.
Théorie différentielle
Certaines fonctions élémentaires possèdent une primitive non élémentaire. Un exemple célèbre est la gaussienne définie par la primitive normalisée de la fonction exp(-x 2/ 2).
Quel que soit le choix de la liste définissant les fonctions élémentaires, il existe toujours des exemples où la primitive ne s'exprime pas en termes de composé algébrique d'éléments de la liste.
La théorie de Galois différentielle permet la détermination de l'ensemble des fonctions élémentaires dont la primitive est encore une fonction élémentaire. Cette théorie étudie des corps particuliers appelés corps différentiels. Ce sont les corps K munis d'une dérivation δ, c'est-à-dire d'une application vérifiant la propriété suivante :
Cette branche traite d'une famille de corps, il est donc naturel de la considérer comme un cas particulier de la théorie de Galois. Cependant l'analogie va plus loin et à bien des égards, cette théorie ressemble à la théorie classique. La différence principale est que, dans ce contexte, le groupe de Galois n'est plus un groupe fini mais en général un groupe algébrique.
Théorie des corps de classes
Article détaillé : Théorie des corps de classes.Voir aussi
Notes
- ↑ Al-Khwarizmi La transposition et la réduction 850
- ↑ Gerolamo Cardano Ars magna, seu de regulis algebrse 1554
- ↑ Carl Friedrich Gauss Disquisitiones arithmeticae 1801
- ↑ Pierre-Laurent Wantzel Recherches sur les moyens de reconnaitre si un problème de Géométrie peut se résoudre avec la règle et le compas 1837
- ↑ Joseph-Louis Lagrange Réflexions sur la résolution algébrique des équations 1770
- ↑ Alexandre-Théophile Vandermonde Mémoire sur la résolution des équations 1771
- ↑ Paolo Ruffini Théorie générale des équation, où il est montré que la résolution de l'équation algébrique général de degré supérieur à quatre est impossible 1799
- ↑ Niels Henrik Abel Mémoire sur les équations algébriques, où l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré 1824
- ↑ Evariste Galois sur les conditions de résolubilité des équations algébriques 1846 Journal de Liouville
- ↑ Joseph Liouville Œuvres Mathématiques d'Évariste Galois Suivie d'un avertissement de Liouville 1846 Journal des Mathématiques pures et appliquées Vol. XI
- ↑ Augustin Louis Cauchy Sur le nombre de valeurs égale ou inégales que peut acquérir une fonction de n variables indépendantes, quand on permute ces variables entre elles d'une manière quelconque 1845
- ↑ Arthur Cayley Sur la théorie des groupes comme dépendance de l'équation symbolique θn = 1. 1854
- ↑ Camille Jordan Traité des substitutions et des équations algébriques 1870
- ↑ Ernst Kummer Über die Zerlegung der aus Wurzeln der Einheit gebildeten complexen Zahlen in ihre Primfactoren 1847
- ↑ Richard Dedekind Sur la théorie des nombres entiers algébriques 1871
- ↑ Heinrich Weber Théorie de Galois 1893
- ↑ Klein Conférences sur l'icosaèdre et les solutions de l'équation du cinquième degré 1877
- ↑ David Hilbert Sur la théorie des corps de nombres quadratiques 1888
- ↑ Emil Artin Théorie de Galois 1942
Liens internes
- Théorie de Galois à l'origine, article retraçant les méthodes mathématiques de l'époque.
Liens externes
- (fr) Mémoire sur les conditions de résolubilité des équations par radicaux (1830), texte de Galois et analyse sur le site BibNum.
- (fr) Les archives de Évariste Galois Bernard Bychan
- (fr) Une courte présentation des extensions algébriques (PDF) par Bernard le Stum Université de Rennes 1 2001
- (fr) Un cours de DEA sur la théorie de Galois (PDF) par Alain Kraus Université de Paris VI 1998
- (fr) Approche très simplifiée du théorème de Galois
- (fr) Colas Bardavid, Théorie de Galois élémentaire (PDF)
- (en) Résumé de la théorie de Galois Excerpted from Beachy/Blair, Abstract Algebra, 2nd Ed
Références
- R. et A. Douady Algèbre et théories galoisiennes Cassini 2005 — ISBN 2-84225-005-2
- S. Lang Algèbre Dunod 2004
- P. Samuel Théorie algébrique des nombres Hermann Paris 1971
- E. Galois Écrits et Mémoires Mathématiques d'Évariste Galois Gauthier-Villars Paris, 1962
- G. Verriest Œuvres Mathématiques d'Évariste Galois Gauthier-Villars Paris, 1951
- J.C. Carrega Théorie des corps Hermann, 1989
- E. Artin Galois Theory Notre Dame Press, Londres 1971
- J. Bewersdorff Galois Theory for Beginners: A Historical Perspective, AMS 2006
- Charles Robert Hadlock, Field theory and its classical problems, Collection : The Carus mathematical monographs 19, The Mathematical Association of America, 2000 (agréable à lire, les pré-requis sont très modestes).
- Ivan Gozard, Théorie de Galois, 2e éd., Paris, Ellipses, 2009.
- Portail des mathématiques
Catégories : Théorie de Galois | Théorie
Wikimedia Foundation. 2010.




