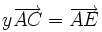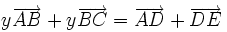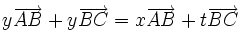- Theoreme de Thales
-
Théorème de Thalès
 Pour l’article homonyme, voir Théorème de Thalès (cercle).
Pour l’article homonyme, voir Théorème de Thalès (cercle). Le théorème de Thalès ou théorème d'intersection est un théorème de géométrie qui affirme que, dans un plan, une droite parallèle à l'un des côtés d'un triangle sectionne ce dernier en un triangle semblable (voir énoncé précis ci-dessous). Dans quelques pays d'Europe, dont la France ce résultat est appelé théorème de Thalès ; en anglais il est connu sous le nom de théorème d'intersection moins commun en Français.
Ce résultat est attribué au mathématicien et philosophe grec Thalès de Milet. Cette attribution s'explique par une légende selon laquelle Thalès aurait calculé la hauteur d'une pyramide en mesurant la longueur de l'ombre au sol de celle-ci et celle de l'ombre d'un bâton de hauteur donnée. Cependant, des documents historiques prouvent que les similitudes des triangles avaient déjà été remarquées par les Babyloniens. Mais la première démonstration écrite retrouvée de ce théorème est donnée dans les Éléments d'Euclide (proposition 2 du livre VI). Cette dernière repose sur la proportionnalité d'aires de triangles de hauteur égale (voir ci-dessous le détail de la preuve).
Le théorème de Thalès se généralise en dimension supérieure. Le résultat est équivalent à des résultats de géométrie projective comme la conservation du birapport par les projections ou encore la propriété de Pappus. À un niveau plus élémentaire, le théorème de Thalès sert à calculer des longueurs en trigonométrie, à condition de disposer de deux droites parallèles. Cette propriété est utilisée dans des instruments de calcul de longueurs.
En anglais et allemand, le théorème de Thalès désigne un autre théorème de géométrie qui affirme qu'un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle.
Sommaire
Énoncés et enseignement
En pratique, le théorème de Thalès permet de calculer des rapports de longueur et de mettre en évidence des relations de proportionnalité en présence de parallélisme.
- Théorème de Thalès :Soit un triangle ABC, et deux points D et E des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC) (comme indiqué sur la figure ci-dessous). Alors on a :
-
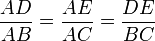 .
.
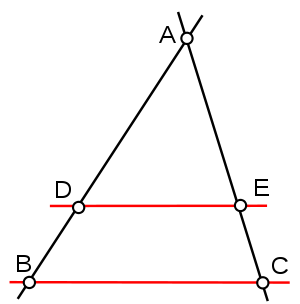
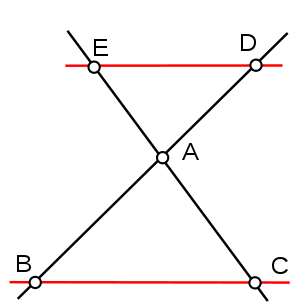
Deux configurations possibles du théorème de Thalès.Le théorème de Thalès démontre que les triangles ABC et ADE sont homothétiques : il existe une homothétie de centre A envoyant B sur D et C sur E. L'un des rapports donnés ci-dessus est au signe près le rapport de l'homothétie. Plus précisément, le rapport de l'homothétie est + AD / AB dans la première configuration et − AD / AB dans la seconde. Le théorème de Thalès est parfois énoncé plus simplement en affirmant qu'une droite parallèle à un des côtés du triangle coupe ce triangle en un triangle semblable.
Il peut être mis en œuvre dans différentes constructions géométriques faisant intervenir compas et règle. Par exemple, il peut justifier une construction permettant de diviser un segment en un nombre donné de parts égales.
Pour être plus rigoureux, l'énoncé ci-dessus donné nécessite l'utilisation d'une distance euclidienne pour donner un sens aux longueurs mentionnées (AB, BC, ...). Un énoncé plus général et précis est donné dans le cadre de la géométrie affine. Dans ce cadre, la notion de longueur est remplacée par celle de mesure algébrique, et seul le rapport a un sens (voir plus loin).
Théorème réciproque
Le théorème de Thalès (en dimension 2), dans son sens direct, permet de déduire certaines proportions dès que l'on connaît un certain parallélisme. Sa réciproque permet de déduire un parallélisme dès que l'on connaît l'égalité de certains rapports.
- Réciproque du théorème de Thalès : Dans un triangle ABC, supposons donnés des points D et E appartenant respectivement au segment [AB] et [AC]. Si les rapports AD/AB et AE/AC sont égaux, alors les droites (DE) et (BC) sont parallèles[réf. nécessaire].
Il est à remarquer que la démonstration de cette réciproque se déduit du théorème. En effet, considérons un point E' du segment [AC] tel que (DE') soit parallèle à (BC). Alors les points A, E', C sont alignés dans cet ordre et AE'/AC = AD/AB = AE/AC donc il vient que AE' = AE. Or il n'existe qu'un seul point situé entre A et C vérifiant cette propriété donc E' = E . Par conséquent, (DE)=(DE') est parallèle à (BC).
Il est à noter que ce qui est appelé "le théorème réciproque de Thalès" n'est pas la réciproque, au sens logique du terme, du théorème initial.
Théorème de la droite des milieux
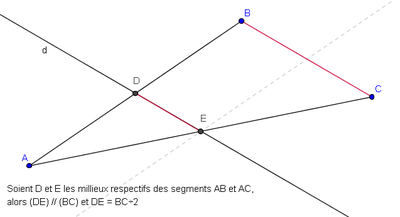
Article détaillé : Théorème des milieux.Le théorème des milieux est une spécialisation du théorème de Thalès, pour laquelle les points D et E correspondent aux milieux des segments [AB] et [AC][réf. nécessaire]. Si une droite passe par les milieux de deux côtés d'un triangle, elle est parallèle à la droite qui supporte le troisième côté ; et la longueur joignant les milieux des deux côtés est égale à la moitié de la longueur du troisième côté:
- Théorème de la droite des milieux : Soit un triangle ABC, et nommons D et E les milieux respectifs de [AB] et [AC]. Alors les droites (DE) et (BC) sont parallèles et on a : 2.DE = BC.
La réciproque du théorème de Thalès justifie que les deux droites sont parallèles ; de plus, le théorème de Thalès s'applique et il vient :
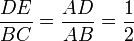 .
.Enseignement et appellations
Ce théorème est connu sous le nom de théorème de Thalès dans l'enseignement des mathématiques en France, en Suisse, etc.[1].
Aucun texte ancien ne semble attribuer la découverte d'un résultat semblable à Thalès. La première référence où une telle attribution est faite est dans les Éléments de géométrie de Rouché et Comberousse en 1883[2]. Une des causes de cette attribution serait l'incitation faite aux agrégatifs à la fin du XIXe siècle siècle d'attribuer aux résultats des noms de mathématiciens pour qu'ils s'intéressent à l'histoire des mathématiques.
C'est aussi sous le nom Théorème de Thalès que le résultat est connu dans les pays de la Méditerranée et dans les pays de l'Europe de l’Est ou du Nord[3]. Cependant, dans les pays de langue anglaise et en Allemagne, ce résultat est connu sous le nom de théorème d'intersection.
L'appellation théorème de Thalès désigne dans ces pays la propriété selon laquelle tout angle inscrit dans un demi-cercle est droit[4] (lire Théorème de Thalès (cercle)).
En Suisse, le théorème est principalement approché grâce à la « petite propriété de Thalès » telle qu'elle est enseignée en France. Le « théorème de Thalès suisse » exprime par contre le carré de la hauteur dans un triangle rectangle.
Origines
Aucune preuve ne peut attester de la connaissance ou non du théorème de Thalès ou d'un résultat similaire avant la (lente) apparition de l'écriture. Les premières traces connues et incontestables de l'utilisation de connaissances mathématiques sont des textes pragmatiques provenant des premières grandes civilisations maitrisant l'écriture. Les textes les plus anciens traitent tous de numération, c'est-à-dire l'art du calcul, particulièrement la multiplication, de la division et de l'extraction de racines. Il n'est pas étonnant que ces textes apparaissent d'abord : sans la maitrise de cet art, le théorème de l'article n'a pas d'utilité[5]. Les premières traces d'une connaissance du théorème ou d'un substitut proche remontent au IIe millénaire av. J.-C. à l'age du bronze à la fois en Égypte antique et en Mésopotamie dans la civilisation babylonienne.
Civilisation babylonienne
Article détaillé : Mathématiques babyloniennes.Durant les fouilles archéologiques aux XIXe siècle et XXe siècle, les premiers textes de mathématiques (et même les premiers textes écrits) ont été retrouvés en Mésopotamie. Dans cette région s'est développée la plus vieille civilisation connue, celle de Sumer, qui développa la première forme d'écriture connue, le sumérien, une écriture cunéiforme constituée de successions de flèches et de pointes. Lui succédèrent les Akkadiens, les Babyloniens et les Assyriens, qui reprirent cette forme d'écriture, ainsi que l'usage du système sexagésimal[6]. Babylone créa une école des scribes : des milliers de tablettes d'argile séchées, en général écrites en sumérien, remplies d'exercices de mathématiques ont été retrouvées et étudiées par les archéologues et historiens des mathématiques depuis les travaux de Hilprecht (vers 1855)[réf. nécessaire].
L'existence de tables numériques et la résolution de problèmes algébriques attestent de fortes connaissances en arithmétique[réf. nécessaire]. En comparaison, peu de tablettes concernent à proprement parler la géométrie. Mais quelques-unes concernent néanmoins les partages de triangles rectangles par lignes droites. Elles mettent en évidence des connaissances sur la similitude des triangles rectangles. Cependant, les problèmes de géométrie sont posés par le dessin d'une figure illustrative ; il n'existe aucune preuve que les notions de parallélisme et d'angle droit ont été formalisées. La tablette de Tell Harmal datant de vers -1800 montre un problème de géométrie avec quatre triangles rectangles imbriqués [7]. Le scribe y met en évidence des relations de proportionnalité entre les cotés.
La tablette MLC 1950 (datée entre -1900 et -1600)[8] décrit un exercice dans lequel le scribe cherche à calculer les longueurs des bases d'un trapèze rectangle à partir d'informations sur l'aire du trapèze, sa hauteur et la hauteur du triangle correspondant. Les données sont indiquées sur la figure ci-contre (en notation sexagésimale). Le scribe calcule :
- la demi-somme des longueurs cherchées comme le rapport de l'aire par la hauteur (d'autres tablettes confirment que la formule donnant l'aire du trapèze était connue[9]) ;
- la demi-différence par application d'une formule non expliquée ; en notant A l'aire du trapèze BDEC, elle s'écrit aujourd'hui littéralement :
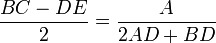 .
.Roger Caritini explique comment obtenir cette formule en appliquant la petite propriété de Thalès aux triangles ABC et ADE d'une part, et aux triangles CBA et CFE d'autre part. Il déduit de ce raisonnement que le scribe possédait « un certain nombre de connaissances dans le domaine de la géométrie élémentaire, en particulier les théorèmes fondamentaux sur la similitude des triangles » (donc, le théorème de Thalès ou un substitut)[10]. Cependant, le problème est présenté par sa figure sans que les hypothèses soient énoncées ;
Démonstration possible de la formule
- Le parallélogramme BDEF admet un angle droit en B, et deux de ses côtés sont par hypothèses parallèles : c'est donc un rectangle. En particulier, la droite (EF) est parallèle à (AB). L'application de la petite propriété de Thalès aux triangles CBA et CFE donne :
-
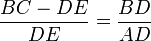 ou encore
ou encore 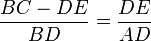 .
. - Comme la droite (DE) est parallèle à la droite (BC), une nouvelle application da la propriété de Thalès donne :
-
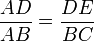 ou encore
ou encore 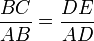 .
. - D'où on peut déduire :
-
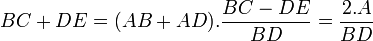 .
. - Par conséquent, on en déduit :
-
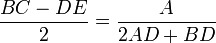 .
.
Égypte antique
Article détaillé : Mathématiques en Égypte antique. Le papyrus Rhind contient un équivalent du théorème de Thalès.
Le papyrus Rhind contient un équivalent du théorème de Thalès.
De la civilisation égyptienne, seuls quatre papyrus offrent des résolutions de problèmes mathématiques. Les égyptologues déduisent les connaissances mathématiques de l'Égypte antique indirectement des documents administratifs traitant des crues du Nil, du calcul des impôts, des répartitions de terres cultivables, du dessin des champs après la destruction des repères suite aux crues[11], ... Selon certains, les pyramides de Gizeh démontreraient un savoir géométrique mis à l'usage de l'architecture[12]. Cependant, selon d'autres, l'absence de tables numériques montre un faible intérêt pour les mathématiques outre les aspects applicatifs[réf. nécessaire].
Le plus célèbre des quatre papyrus est le papyrus Rhind nommé d'après Alexander Henry Rhind (1833-1863), un antiquaire écossais qui l'achète en 1858. Il aurait été écrit par le scribe Ahmès sous le pharaon Apophis Âa-ouser-rê (vers -1550) reprenant le contenu d'un papyrus non retrouvé écrit sous le règne du pharaon Amenemhat II (vers -1850).
Sylvia Couchoud, une égyptologue étudie[13] ce papyrus avec attention. Outre les informations qu'il fournit sur les connaissances en arithmétique et en algèbre, il offre l'énoncé du théorème de Thalès, appelé seqet[14], appliqué à un exemple numérique.
Grèce antique
La civilisation grecque antique est différente de celle de l'Égypte ou de Babylone. La philosophie et la beauté y sont des sujets essentiels. Il n'est donc pas étonnant que les mathématiques grecques n'ont plus, pour premier objectif, la résolution de problèmes pragmatiques mais théoriques[15]. Pythagore établit une géométrie fondée sur des principes, qui deviendront plus tard des axiomes pour accéder à une approche non expérimentale mais purement spéculative et intellectuelle[16]. Pour Platon, les mathématiques constituent la base de l'enseignement des Rois-philosophe de la cité idéale[17]. La géométrie prend réellement ses racines dans la civilisation grecque.
Une vision de cette nature modifie radicalement la formulation du théorème de Thalès, dont on trouve la première démonstration écrite connue dans les Eléments d'Euclide[18]. Trois éléments essentiels ont changé. Le théorème est énoncé de manière parfaitement générale, à la différence des égyptiens qui décrivent ce résultat à l'aide d'un exemple, ou des Babyloniens qui semblent utiliser implicitement le résultat. Il est démontré, précédemment les traités de mathématiques se présentaient comme une suite de techniques à même de trouver le bon résultat. La notion de démonstration était absente. Enfin la réciproque est énoncée, ce qui est aussi une première.
Le calcul de la hauteur d'une pyramide, une légende
 le théorème de l'article doit son nom en France à Thalès de Milet.
le théorème de l'article doit son nom en France à Thalès de Milet.
Des textes littéraires de l'Antiquité grecque font référence aux travaux de Thalès de Milet au VIe siècle av. J.-C., dont aucun écrit ne nous est parvenu. Cependant, aucun texte ancien n'attribue la découverte théorème à Thalès[19]. Dans son commentaire des Éléments d'Euclide, Proclos[20] affirme que Thalès aurait rapporté le résultat de son voyage en Égypte. Hérodote rapporte la même chose et précise qu'il est un des sept sages fondateurs de cette civilisation[21]. Une anecdote célèbre rapporte que Thalès obtint l'admiration de Pharaon en mesurant la hauteur d'une des pyramides. Plutarque indique que :
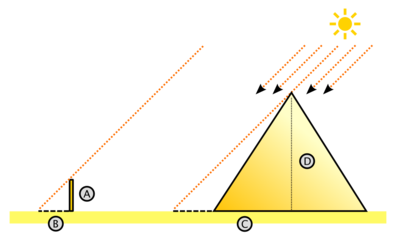
« Dressant seulement à plomb un bâton au bout de l’ombre de la pyramide et se faisant deux triangles avec la ligne que fait le rayon du soleil touchant aux deux extrémités, tu montreras qu’il y avait telle proportion de la hauteur de la pyramide à celle du bâton, comme il y a de la longueur de l’ombre de l’un à l’ombre de l’autre[22]. »
Cette légende est reprise par d'autres auteurs. Diogène Laërce écrit :
« Hiéronyme dit que Thalès mesura les pyramides d'après leur ombre, ayant observé le temps où notre propre ombre égale notre hauteur.[23]. »
Bernard Vitrac met de sérieux doutes sur la réalité des précisions : « Plus ils sont tardifs plus ils sont capables de donner des détails sur le procédé utilisé »[24]. Plutarque parle juste de proportionnalité entre les hauteurs de la pyramide et du bâton d'une part, des longueurs de leurs ombres projetées d'autre part. Laërce évoque l'égalité des côtés adjacents à un angle droit d'un triangle rectangle isocèle. La légende selon laquelle Thalès aurait inventé "son" théorème en voulant calculer la hauteur d'une pyramide est aujourd'hui véhiculée et brodée par de nombreux sites internet, de nombreux journaux de vulgarisations, et par certains auteurs[25].
Selon Michel Serres, cette histoire était utilisée et transmise dans la civilisation grecque antique comme un moyen mnémotechnique de se rappeler le résultat : « Dans une culture de tradition orale, récit tient lieu de schéma, scène vaut intuition, où l'espace vient en aide à la mémoire. [...] Mieux vaut reconnaître, alors, dans le récit, moins une légende originaire que la forme même de la transmission ; il communique un élément de science plus qu'il ne témoigne de son émergence »[26].
Cette histoire atteste aussi de l'origine probable de la géométrie : le calcul des distances et des tailles caractéristiques d'objets inaccessibles (ici la hauteur d'une pyramide) a probablement conduit l'homme à s'interroger sur les relations des distances entre des points de repère. Cette interrogation l'a naturellement conduit à s'intéresser à la trigonométrie, d'où l'émergence de résultats comparables au théorème de Thalès[27]. Par ailleurs, dans les différentes versions est utilisé un objet de référence, un axe, un essieu, ou Thalès lui-même, utilisé comme un gnomon, terme signifiant instrument du savoir, de la compréhension. Certains voient dans l'origine babylonienne de ce terme une preuve supplémentaire que l'énoncé du théorème et sa démonstration soient d'origine babylonienne[28]
Une version de l'histoire brodée de la découverte du résultat par Thalès pourrait être la suivante.
Version de la légende
- Lors d'un voyage en Égypte, Thalès aurait visité les pyramides construites plusieurs siècles plus tôt. Admirant ces monuments, il aurait été mis au défi d'en calculer la hauteur. Thalès aurait entrepris donc une mesure des pyramides, dont le principe reposerait sur le concept de triangles semblables et de proportionnalité. Thalès aurait remarqué qu'à cette époque de l'année, à midi, l'ombre portée d'un homme ou d'un bâton égalait la taille de l'homme ou la longueur du bâton. Les rayons de soleil pouvant être supposés parallèles, Thalès en aurait déduit qu'il en serait de même pour la hauteur de la pyramide et son ombre projetée.
- Encore fallait-il être capable de mesurer l'ombre projetée : il aurait repéré le sommet de l'ombre projetée de la pyramide mais pour la mesurer dans son entier, il lui aurait fallu partir du centre de la pyramide qui n'était pas accessible. Thalès aurait bénéficié d'un atout supplémentaire : non seulement l'ombre portée égalait la hauteur de la pyramide mais les rayons du soleil étaient perpendiculaire à une arête de la base. Le sommet de l'ombre de la pyramide se serait trouvé alors sur la médiatrice d'un côté de la base. Il lui aurait suffit de mesurer la distance séparant l'extrémité de l'ombre et le milieu du côté, d'ajouter à cette longueur un demi-côté pour obtenir la hauteur de la pyramide.
- Le fait que le sommet de l'ombre de la pyramide soit sur la médiatrice d'un côté à midi ne tient absolument pas du hasard mais du fait que les pyramides sont orientées plein sud ou plein ouest. La pyramide de Khéops est située à une latitude de 30°, la longueur de l'ombre égale celle du bâton lorsque le soleil fait 45° avec la verticale. L'angle que forme le soleil avec la verticale varie au cours de l'année entre 6,73° (au plus fort de l'été) et 53,27° (au plus fort de l'hiver) et ne fait un angle de 45° que deux fois dans l'année (le 21 novembre et le 20 janvier). Ce serait un hasard extraordinaire que Thalès se fût trouvé là à cet instant précis. À toute autre période de l'année, la longueur de l'ombre est proportionnelle à la hauteur.
- Thalès aurait lui-même mentionné ces remarques. Il serait retourné et aurait expliqué que la hauteur de la pyramide est proportionnelle à la longueur de son ombre. En comparant la longueur de l'ombre et la hauteur d'un bâton planté, il lui aurait été facile de connaître le coefficient de proportionnalité et de l'appliquer ensuite à l'ombre de la pyramide pour en déterminer sa hauteur. Plutarque ne dit d'ailleurs pas autre chose(ou?).
Démonstrations
Preuve mentionnée par Euclide
Dans l'approche d'Euclide, les points sont des éléments indivisibles à partir desquels les objets géométriques se définissent. Dans cette perspective, les notions de segments et de droites ne sont pas différenciées. La propriété démontrée par Euclide n'est pas exactement le théorème comme il est cité de nos jours. Une traduction datant de 1632 est la suivante :
Livre VI, Proposition 2 : « Si on mène une ligne droite parallèle à l'un des cotez d'un triangle, laquelle coupe les deux autres cotez ; elle les coupera proportionnellement ; & si les deux cotés d'un triangle sont coupés proportionnellement, la ligne coupante sera parallèle a l'autre cotez[29]. »
Si on mène une ligne droite parallèle à l'un des côtés d'un triangle, laquelle coupe les deux autres côtés, elle les coupera proportionnellement. Et si les deux côtés d'un triangle sont coupés proportionnellement, la ligne coupante sera parallèle à l'autre côté.Les données de ce théorème sont donc :
- Un triangle, par définition délimité par trois lignes droites (segments) AB, BC, et CA ;
- Une ligne droite DE parallèle à la ligne droite BC intersectant AB en D et AC en E.
Les notations sont celles introduites par Euclide après l'énoncé ; l'illustration ci-contre donne la disposition des points. La conclusion donnée est :
« AD fera à DB ce que AE est à EC. »
Autrement dit, en écriture mathématique actuelle :
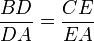 .
.La démarche d'Euclide se base sur le fait que l'aire d'un triangle est égale à la moitié de la longueur de sa hauteur, par-rapport à une base (ou côté) quelconque, multipliée par la longueur de la base en question. Il constate que les hauteurs des triangles DEB et DEC par rapport à leur base commune DE ont la même longueur. Ces deux triangles ont par conséquent la même aire, et a fortiori, ils ont donc le même ratio (d'aires) avec n'importe quelle aire non nulle, et en particulier celle du triangle DEA. Comme les hauteurs des triangles DEB et DEA par rapport, respectivement, aux bases BD et DA, sont confondues, Euclide en déduit que le ratio de DEB par DEA est le même que le ratio de BD par DA. Par analogie, le ratio de DEC par DEA est le même que le ratio de CE par EA. La proposition 11 du livre V énonce que les ratios qui sont les mêmes qu'un autre ratio sont les mêmes. Euclide en déduit donc que le ratio de BD par DA est le même que le ratio de CE par EA.
Le raisonnement proposé par Euclide se traduit aujourd'hui par les égalités suivantes :
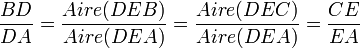 .
.Les égalités s'appuient sur les constatations suivantes :
- Les triangles DEB et DEA ont une hauteur commune h issue de E. Donc, leur aire est respectivement ½BD×h et ½DA×h.
- Les triangles DEB et DEC ont une base commune DE, et les sommets opposés B et C sont par hypothèses sur une droite parallèle à (DE).
- Enfin, les triangles DEC et DEA ont une hauteur commune h' issue de D. Donc, leur aire est respectivement ½CE×h' et ½EA×h'.
Sous forme de tableau de proportionnalité :
BD DEB DEC CE DA DEA DEA EA Preuve purement vectorielle
Il faut se poser la question de la validité d'une démonstration vectorielle du théorème de Thalès. En effet, la géométrie vectorielle s'appuie souvent sur une définition géométrique des vecteurs, définition dans laquelle le théorème de Thalès joue un rôle prépondérant quand il s'agit d'affirmer que
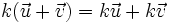 .
.Mais on peut toutefois s'intéresser à une écriture possible du théorème de Thalès et sa justification grâce aux opérations vectorielles. Ce qui pourrait permettre de généraliser le théorème de Thalès à tout espace affine euclidien associé à un espace vectoriel.
Dire que D est sur (AB) c'est écrire qu'il existe un réel x tel que
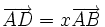 .
.De même, dire que E est sur (AC), c'est écrire qu'il existe un réel y tel que
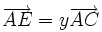 .
.Enfin, dire que les droites (ED) et (BC) sont parallèles, c'est écrire qu'il existe un réel t tel que
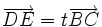 .
.Les égalités précédentes et la relation de Chasles permettent d'écrire que :
L'écriture suivant les vecteurs
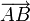 et
et 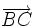 se doit d'être unique car ces vecteurs ne sont pas colinéaires. Donc
se doit d'être unique car ces vecteurs ne sont pas colinéaires. Donc 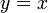 et
et 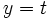
On obtient donc les trois égalités:
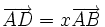
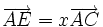
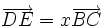 .
.
L'avantage de cet énoncé et de cette démonstration est que cela n'oblige pas à traiter les différents cas de configuration évoqués plus haut.
Généralisations du théorème de Thalès
Cas de trois droites parallèles
Toujours en dimension 2, le théorème de Thalès peut s'énoncer de manière équivalente :
- Théorème de Thalès :[réf. nécessaire] Soient deux droites d et d' (du plan réel euclidien) et trois droites parallèles (AA'), (BB') et (CC') intersectant d et d' respectivement en A et A', en B et B', et en C et C', comme indiqué sur la figure ci-contre. Alors :
-
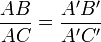 .
.
Cette conclusion équivaut à l'une des deux égalités suivantes :
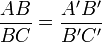 ou
ou 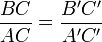 ;
;ou encore à :
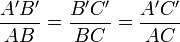 .
.Le premier énoncé donné du théorème de Thalès est la spécialisation du second au cas où deux points sont confondus (en général A et A'). En considérant la parallèle à d' passant par A le second énoncé se déduit du premier.
Dimensions supérieures à 2
Souvent énoncé comme un théorème de géométrie plane, le théorème de Thalès se généralise sans difficulté en dimension supérieure, notamment en dimension 3. L'utilisation de droites parallèles est remplacée par des hyperplans parallèles ; les droites (d) et (d') n'ont pas à être supposées coplanaires :
- Théorème de Thalès[30] : Soient (d) et (d') deux droites d'un même espace affine ; et Ha, Hb et Hc trois hyperplans parallèles. On suppose en outre que la droite (d) intersecte les hyperplans respectivement en A, B, C, et de même que la droite (d') respectivement en A', B' et C'. Alors, on a :
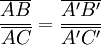
Cependant, la preuve mentionnée par Euclide, qui utilise explicitement la notion d'aire, est propre à la dimension 2 et ne se généralise pas à la dimension supérieure. De même, il n'y a pas de réciproque évidente à cet énoncé général. Dans une note[31], où est mentionnée une réciproque donnant l'existence d'hyperplans parallèles.
Preuve utilisant une projection affine
Dans son livre, Marcel Berger propose une preuve algébrique de la version du théorème de Thalès en dimension supérieure[32]. Sa preuve ne s'appuie pas sur une approche axiomatique de la géométrie, mais sur la définition actuelle d'espace affine et vectoriel.
La preuve de Marcel Berger consiste à construire une bijection affine f entre les deux droites d et d' envoyant A sur A', B sur B', et C sur C'. Il est possible de déduire de la définition d'une application affine qu'une bijection affine entre droites affines préserve le rapport. Donc :
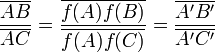
Pour construire effectivement f, Marcel Berger propose de munir l'ensemble des hyperplans parallèles à Ha d'une structure de droite affine (structure quotient), de sorte que l'application qui à un point de d (ou bien de d') associe l'hyperplan passant par ce point et parallèle à Ha soit une application affine. Sans introduire la notion d'espace quotient, on peut aussi[33] définir l'application f comme la restriction à d de la projection sur la droite d' parallèlement à Ha. Par définition, f envoie effectivement A sur A', B sur B', et C sur C'. L'inverse de f se définit comme la restriction à la droite d' de la projection sur d parallèlement à Ha.
Conservation des birapports par les projections
Le birapport est un invariant projectif associé à quatre points. Le théorème de conservation des birapports par projection est lié de près au théorème de Thalès, l'un pouvant sans grand mal se déduire de l'autre[34].
De même que les trois droites parallèles du théorème de Thalès peuvent être remplacées par des hyperplans parallèles dans un espace affine de dimension supérieure à 2, les quatre droites concourantes de ce théorème de conservation des birapports peuvent être remplacées par des hyperplans appartenant à un même faisceau en dimension supérieure.
L'intérêt de ce point de vue est de souligner l'analogie du « rapport »
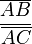 intervenant dans le théorème de Thalès avec le birapport utilisé en géométrie projective : le premier est laissé invariant par une transformation affine d'une droite affine vers une autre exactement comme le second est laissé invariant par une transformation projective d'une droite projective vers une autre.
intervenant dans le théorème de Thalès avec le birapport utilisé en géométrie projective : le premier est laissé invariant par une transformation affine d'une droite affine vers une autre exactement comme le second est laissé invariant par une transformation projective d'une droite projective vers une autre.Le théorème de Thalès dans les plans arguésiens
Il est également possible de donner une démonstration du théorème de Thalès à partir de l'axiomatique des plans affines dégagée au XXe siècle ; si on prend le parti de présenter les plans affines (sur un corps commutatif) comme les plans arguésiens vérifiant la propriété de Pappus, le théorème de Thalès peut être prouvé[35].
Applications du théorème de Thalès
Algèbre géométrique
Le théorème de Thalès offre des égalités entre diverses fractions. Si les droites et les triangles appartiennent à la branche mathématique appelée géométrie, les fractions font partie de l'algèbre. Le fait que le théorème de Thalès offre des égalités sur les fractions en fait une méthode de démonstration qui s'applique à l'algèbre. Il est possible d'établir toutes les lois régissant le comportement des fractions et par là, les mécanismes qui permettent de venir à bout de toutes les équation du premier degré. Cette démarche est décrite dans l'article Algèbre géométrique.
Résultats de géométrie projective et rapport avec les homothéties
En géométrie, le théorème de Thalès ou sa réciproque peuvent être utilisés pour établir des conditions d'alignement ou de parallélisme. Sans faire appel aux notions de droite projective, ils permettent d'obtenir des versions satisfaisantes des résultats relevant en réalité de la géométrie projective. Le théorème de Thalès peut être utilisé comme substitut des homothéties dans les démonstrations.
- Théorème de Ménélaüs : Étant donnés un triangle ABC et trois points A', B' et C' appartenant respectivement aux droites (BC), (AC) et (AB) ; les points A', B' et C' sont alignés si :
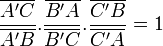
- Théorème de Ceva : Étant donnés un triangle ABC et trois points A', B' et C' appartenant respectivement aux droites (BC), (AC) et (AB) ; les droites (AA'), (BB') et (CC') sont concourantes ou parallèles ssi :
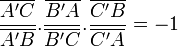
- Théorème de Pappus : Soient deux droites d et d' ; trois points A, B et C de d ; trois points A', B', et C' de d'. On note P, Q, et R les intersections respectives de (AB') et (A'B), de (B'C) et (BC'), et de (AC') et (A'C). Alors les points P, Q et R sont alignés.
- Théorème de Desargues : Soient deux triangles ABC et A'B'C' tels que les droites (AB) et (A'B') sont parallèles, de même pour (BC) et (B'C') et pour (AC) et (A'C'). Alors les droites (AA'), (BB') et (CC') sont parallèles ou concourantes.
Nombres constructibles
Article détaillé : Nombre constructible.Une question qui s'est soulevée durant l'Antiquité, et notamment sous la forme du problème de la quadrature du cercle, est la possibilité de construire une figure à l'aide de la règle (non graduée) et du compas :
- La règle est un instrument idéalisé permettant de considérer une droite passant par deux points déjà tracés ;
- Le compas est un instrument idéalisé permettant de considérer un cercle de centre un point déjà construit et de rayon le report d'une distance réalisée entre deux points déjà construits.
Un point du plan euclidien est dit constructible à la règle et le compas s'il peut être obtenu par un nombre fini d'étapes à partir des points de coordonnées (0,0) et (0,1). Suite aux travaux de Georg Cantor, il peut être affirmé que tous les points constructibles à la règle et au compas sont en nombre dénombrable.
Un nombre constructible est un nombre réel qui peut être obtenu comme coordonnée d'un point constructible. L'ensemble des nombres constructibles est stable par somme, produit et inverse. Le théorème de Thalès montre que le produit de deux nombres constructibles est un nombre constructible. En effet, pour deux réels non nuls constructibles x et y, un calcul donne la justification de la construction ci-contre :
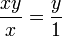
Notes
- ↑ . Plus précisément le résultat dans la première configuration et le théorème de la droite des milieux sont enseignées dès la classe de quatrième française et le « théorème de Thalès » à proprement parler et sa réciproque dans la classe de troisième française cf. Rapport L'enseignement des sciences mathématiques (mars 2002), p.162. Des constructions géométriques mettant en œuvre le théorème doivent être vues au collège. Le lien entre le théorème de Thalès et les homothéties doit être enseigné seulement au lycée. Dans son rapport, Jean-Pierre Kahane critique ouvertement l'absence du cas d'égalité des triangles dans l'enseignement des mathématiques en France, dont il tient comme responsable la réforme dite des « mathématiques modernes »Rapport L'enseignement des sciences mathématiques, pp. 113 et 163.
- ↑ Un site apportant quelques éléments d'information sur l'histoire de l'appellation du théorème.
- ↑ Vérification par les interwikis.
- ↑ Courte présentation des différents énoncés nommés selon Thalès.
- ↑ G Ifrah A universal history of numbers : From prehistory to the invention of the computer Harvill Press London 1998 ISBN 1-86046-324-X
- ↑ C. Proust Le calcul sexagésimal en Mésopotamie REHSEIS 2005 lire
- ↑ Un site en italien présentant différentes tablettes babyloniennes, paragraphe 8.
- ↑ Ibid, paragraphe 10, Il theorema di Talete.
- ↑ Par exemple, la tablette YBC 7290.
- ↑ Roger Caratini, Les mathématiciens de Babylone, Presses de la Renaissance, Paris, 2002 ; pp. 238-243.
- ↑ A. Erman H. Ranke La Civilisation égyptienne,Payot Paris 1985 (ISBN 2-228-88800-1)
- ↑ J O'Connor E. F. Robertson An overview of Egyptian mathematics 2000
- ↑ Sylvia Couchoud Mathématiques Égyptiennes. Recherches sur les connaissances mathématiques de l’Égypte pharaonique, éditions Le Léopard d’Or 2004 (ISBN 2-863-777-118-3)
- ↑ Webmath Une courte histoire des mathématiques
- ↑ Bernard Vitrac L'origine de la géométrie grecque Génies de la Science Nov 2004 Lire
- ↑ Proclos Commentaire sur le premier livre des Éléments d'Euclide 65 11
- ↑ Platon La république Chapitre VII Lire sur le site de David E. Joyce.
- ↑ Euclide Eléments d'Euclide livre VI proposition 2 Lire en page 215 ou Lire
- ↑ Proportionnalité en géométrie plane dans les Éléments d'Euclide, article de Éliane Cousquer.
- ↑ Proclos Commentaire sur le premier livre des Eléments d’Euclide Trad. franç. P. Ver Eecke. Bruges, Desclée de Brouwer 1948
- ↑ Hérodote, Histoires [détail des éditions] [lire en ligne]
- ↑ Plutarque Le banquet des sept sages lire
- ↑ Diogène Laërce Vie, doctrine et sentence des philosophes illustres ; Thalès, I, 27.
- ↑ Bernard Vitrac, L'origine de la géométrie grecque Génies de la Science Nov 2004 Lire
- ↑ Claude Allègre reprend cette histoire pour argent comptant dans son livre Un peu de science pour tout le monde, Fayard, 2006.
- ↑ Michel Serres, Les origines de la géométrie, Flammarion 1995.
- ↑ Ibid, pp.220-230.
- ↑ Ibid., pp. 235-237 ; 239 ; 245.
- ↑ Disponible sur Gallica : [1].
- ↑ Ce paragraphe présente la version du théorème qu'on pourra lire par exemple dans le traité de Géométrie de Marcel Berger, énoncé 2.5.1 (tome 1, p. 73 dans l'édition de 1979 - CEDIC Fernand Nathan).
- ↑ Voir par exemple une note à l'usage des étudiants préparant le CAPES, par Jérôme Germoni, p. 4, disponible en ligne sur le site de l'Université de Lyon 1 (consultée le 1er octobre 2007).
- ↑ Lire proposition 2.5.1.
- ↑ Claude Tisseron, Géométries affine, projective et euclidienne, Hermann, pp. 56-57.
- ↑ Ainsi le traité de Géométrie de Marcel Berger, énoncé 6.5.5 (tome 1, p. 163 dans l'édition de 1979 - CEDIC Fernand Nathan) explique comment déduire Thalès de cette propriété projective et constitue d'ailleurs la source de ce paragraphe. On trouvera dans l'autre sens des éléments de démonstration du théorème projectif à partir de Thalès à l'article Faisceau harmonique.
- ↑ On pourra en lire un énoncé et une preuve dans un cours pour enseignants (en allemand) de W. Börner, p. 16 disponible en ligne sur le site de l'Université d'Iéna (consulté le 1er octobre 2007).
Voir aussi
- Livre VI des Éléments d'Euclide
- Théorème des milieux : cas particulier du théorème de Thalès.
 Wikibooks possède des exercices sur le théorème de Thalès.
Wikibooks possède des exercices sur le théorème de Thalès.
Liens et documents externes
- Le théorème de Thalès
- Le théorème de Thalès et sa réciproque
- Une animation sur le théorème de Thalès
- Construction du nombre 3/7 à la règle et au compas (animation InstrumenPoche)
- Portail de la géométrie
Catégories : Bon article | Ligne droite | Théorème de mathématiques | Géométrie | Théorème de géométrie | Géométrie du triangle | Mathématiques élémentaires
Wikimedia Foundation. 2010.