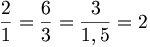- Proportionnalite
-
Proportionnalité

Cet article fait partie de la série
Mathématiques élémentairesAlgèbre Logique Arithmétique Probabilités Statistiques On dit que deux mesures sont proportionnelles quand on peut passer de l'une à l'autre en multipliant ou en divisant par une même constante. Dans le cas où l'on multiplie, cette constante est appelée coefficient de proportionnalité.
Exemple: Si, dans un magasin, le prix des pommes est de 2 euros le kg, il y a proportionnalité entre le prix à payer et le poids de pommes achetées. Le coefficient de proportionnalité est 2.
- Pour 1 kg, on doit payer 2 euros.
- Pour 3 kg, on doit payer 6 euros.
- Pour 1,5 kg, on doit payer 3 euros.
On remarque que le quotient des deux quantités est constant et est égal au coefficient de proportionnalité.
Les Anciens comme Euclide auraient écrit que 2 est à 1 comme 6 est à 3 ou comme 3 est à 1,5.
Sommaire
Tableau de proportionnalité
C'est un tableau où l'une des lignes est proportionnelle à l'autre.
poids 1 3 1,5 prix 2 6 3 On peut ajouter une colonne à un tableau de proportionnalité en additionnant deux colonnes, ou en multipliant une colonne par une constante.
- 3 + 1,5 = 4,5 et 6 + 3 = 9 donc
poids 1 3 1,5 4,5 prix 2 6 3 9 - 3 × 2 = 6 et 6 × 2 = 12 donc
poids 1 3 1,5 6 prix 2 6 3 12 Si on choisit deux colonnes, le produit des nombres situés dans une diagonale est égal au produit des nombres situés dans l'autre diagonale (produit en croix)
3 1,5 6 3 3 × 3 = 6 × 1,5
Quatrième proportionnelle
La quatrième proportionnelle est le quatrième nombre à mettre dans un tableau de proportionnalité dont 3 cases sont déjà remplies. Ce quatrième nombre s'obtient en faisant le produit des nombres situés sur une même diagonale et en divisant par le troisième nombre.
Cette technique s'est appelée longtemps la règle de trois.
Exemple: il faut 6 heures pour écrire un rapport de 33 pages, combien d'heures faut-il pour un rapport de 55 pages?
Tableau de proportionnalité:
33 55 6 ? Réponse:
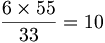 heures
heuresProportionnalité et géométrie
La proportionnalité en géométrie est principalement utilisée dans le théorème de Thalès et dans les triangles semblables. Mais on la retrouve aussi dans les coordonnées de vecteurs colinéaires. En dimension 2, l'égalité des produits en croix ab' = ba' devient alors ab' - ba'= 0 (déterminant nul)
Représentation graphique
Si y est proportionnel à x, les points de coordonnées (x;y) sont tous situés sur une même droite passant par l'origine. Le coefficient de proportionnalité, le réel k tel que y = k×x est appelé pente ou coefficient directeur de la droite. On dit aussi que y est fonction linéaire de x.
Quantités inversement proportionnelles
Deux quantités sont inversement proportionnelles, si l'une est proportionnelle à l'inverse de l'autre.
Pour parcourir 100 km, le temps est inversement proportionnel à la vitesse.
- à 100 km.h-1, il faut 1 h
- à 50 km.h-1, il faut 2 h
- à 10 km.h-1, il faut 10 h
On remarque que, si deux quantités sont inversement proportionnelles, leur produit est constant
- 100 × 1 = 50 × 2 = 10 × 10
Voir aussi
- Portail des mathématiques
Catégorie : Mathématiques élémentaires
Wikimedia Foundation. 2010.