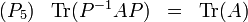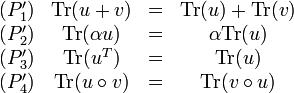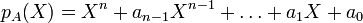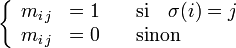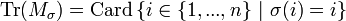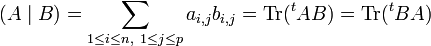- Trace (algebre)
-
Trace (algèbre)
 Pour les articles homonymes, voir Trace.
Pour les articles homonymes, voir Trace.En algèbre linéaire, la trace d'une matrice carrée est définie comme la somme de ses éléments diagonaux ; la trace est une forme linéaire sur l'ensemble des matrices. Il est également possible de définir la trace d'un endomorphisme d'un espace vectoriel de dimension finie.
La trace est un outil utilisé dans de nombreuses branches des mathématiques. On la trouve en théorie de Galois où elle est à l'origine de la définition de la forme trace. Cette forme est aussi utilisée en théorie algébrique des nombres, par exemple pour définir le discriminant d'un anneau d'entiers algébriques. Dans le cadre des représentations d'un groupe fini elle est à la base de la définition du caractère. Cette théorie permet de mieux comprendre la structure d'un groupe. En conséquence, on retrouve l'utilisation de cet outil dans la démonstration de théorèmes sur le sujet, comme par exemple celui de Burnside sur un groupe résoluble ou celui sur le problème de Burnside.
Dans tout l'article on considère des matrices à coefficients dans un corps
 .
.Sommaire
Trace d'une matrice carrée
Étant donnée une matrice carrée
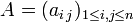 , on note sa trace Tr(A) et on la définit comme égale au scalaire :
, on note sa trace Tr(A) et on la définit comme égale au scalaire : (on peut d'ailleurs généraliser cette définition à la trace d'une matrice n x m :
(on peut d'ailleurs généraliser cette définition à la trace d'une matrice n x m : 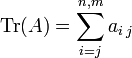 )
)
Pour toutes matrices carrées A et B (de même ordre) et pour tout scalaire
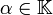 , les propriétés suivantes sont vérifiées :
, les propriétés suivantes sont vérifiées :Autrement dit la trace est une forme linéaire sur l'espace vectoriel
 des matrices carrées d'ordre n donné (propriétés 1 et 2), invariante par transposition (propriété 3).
des matrices carrées d'ordre n donné (propriétés 1 et 2), invariante par transposition (propriété 3).La propriété 4 a pour corolaire[1] important l'égalité suivante, valable pour toute matrice carrée A et pour toute matrice inversible P de même ordre :
Autrement dit la trace est un « invariant de similitude » pour les matrices carrées d'ordre donné. C'est cette propriété qui va nous permettre de définir la trace d'un endomorphisme « abstrait ». La réciproque de ce résultat est vraie en ce sens : toute forme linéaire sur l'espace des matrices carrées, invariante par similitude est proportionnelle à la trace.
D'autre part, la propriété 4 reste valable pour des matrices rectangulaires :
Trace d'un endomorphisme
On se donne un espace vectoriel E de dimension finie et un endomorphisme
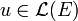 ; on veut définir la trace de u. Dès que l'on fixe une base
; on veut définir la trace de u. Dès que l'on fixe une base  de E, on peut donner la représentation matricielle de u relativement à
de E, on peut donner la représentation matricielle de u relativement à  : c'est une matrice A. On est tenté de définir la trace de u comme étant égale à celle de A.
: c'est une matrice A. On est tenté de définir la trace de u comme étant égale à celle de A.Le problème est que cette définition dépend a priori du choix initial de la base
 . La question est donc : la valeur ainsi définie dépend-t-elle vraiment du choix de la base ? Autrement dit, arrive-t-on à une valeur différente de la trace de u si on la calcule dans une autre base
. La question est donc : la valeur ainsi définie dépend-t-elle vraiment du choix de la base ? Autrement dit, arrive-t-on à une valeur différente de la trace de u si on la calcule dans une autre base  ? La réponse est heureusement non et ce grâce à la propriété 5 ci-dessus.
? La réponse est heureusement non et ce grâce à la propriété 5 ci-dessus.En effet si on note A' la matrice de u dans la nouvelle base
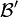 , on a la relation dite « de changement de base » : A' = P − 1AP, où P désigne la matrice de passage de la base
, on a la relation dite « de changement de base » : A' = P − 1AP, où P désigne la matrice de passage de la base  à la base
à la base 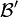 . Or d'après la propriété 5 : Tr(P − 1AP) = Tr(A), donc Tr(A') = Tr(A). Ainsi notre définition de la trace de u est intrinsèque c'est-à-dire indépendante du choix d'une base particulière pour son calcul. On la notera Tr(u).
. Or d'après la propriété 5 : Tr(P − 1AP) = Tr(A), donc Tr(A') = Tr(A). Ainsi notre définition de la trace de u est intrinsèque c'est-à-dire indépendante du choix d'une base particulière pour son calcul. On la notera Tr(u).On peut assez naturellement adapter les premières propriétés de la trace d'une matrice carrée à la trace d'un endomorphisme. Pour tous endomorphismes
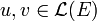 et pour tout scalaire
et pour tout scalaire 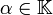 les propositions suivantes sont vérifiées :
les propositions suivantes sont vérifiées :De plus, pour
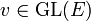 (c'est-à-dire que v est un automorphisme) :
(c'est-à-dire que v est un automorphisme) :Autrement dit la trace est une forme linéaire sur l'espace vectoriel
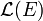 , invariante par transposition et par conjugaison.
, invariante par transposition et par conjugaison.Propriétés
Toutes les propriétés qui suivent sont énoncées uniquement dans le cas des matrices carrées ; les énoncés parallèles pour les endomorphismes s'en déduisent facilement.
Trace et polynôme caractéristique
Considérons une matrice carrée A d'ordre n et notons pA son polynôme caractéristique. On peut écrire
La trace de A apparaît alors naturellement dans le développement de pA puisqu'on a la relation :
- an − 1 = − Tr(A).
Trace et réduction
Dans le cas où une matrice carrée A est trigonalisable (et a fortiori lorsqu'elle est diagonalisable) on peut donner une relation simple entre la trace de A et ses valeurs propres. Notons
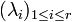 ces valeurs propres et
ces valeurs propres et 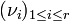 leurs ordres de multiplicité respectifs. Alors on a :
leurs ordres de multiplicité respectifs. Alors on a : .
.
On peut obtenir cette relation en trigonalisant la matrice et en appliquant l'invariance de la trace par similitude, mais aussi en appliquant les relations entre coefficients et racines au polynôme caractéristique et en appliquant la propriété précédente.
Trace de la matrice d'une permutation
On peut représenter une permutation
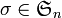 (où
(où 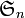 représente le groupe symétrique d'ordre
représente le groupe symétrique d'ordre 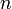 ) par une matrice
) par une matrice 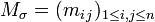 carrée d'ordre
carrée d'ordre 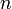 , définie par :
, définie par :La trace de la matrice Mσ s'interprète alors comme le nombre de points fixes de la permutation σ :
Produit scalaire canonique
Soit
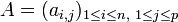 et
et 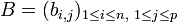 deux matrices dans
deux matrices dans 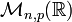 . On remarque que
. On remarque queOn dispose ainsi d'une écriture agréable du produit scalaire canonique.
Avec cette définition, il apparait clairement que les matrices symétriques et les matrices antisymétriques forment deux sous-espaces orthogonaux de l'ensemble des matrices carrées.
Divers
- La trace de la matrice identité d'ordre n est donnée par : Tr(In) = n.
- L'ensemble formé des matrices de trace nulle est un hyperplan de l'espace vectoriel des matrices carrées d'ordre n donné.
- Soit E un
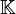 -espace vectoriel de dimension n,
-espace vectoriel de dimension n, 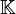 étant un corps de caractéristique 0, et u un endomorphisme de E. Si
étant un corps de caractéristique 0, et u un endomorphisme de E. Si 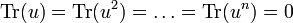 alors un = 0.
alors un = 0. - La trace d'un projecteur p est égale à son rang : Tr(p) = rg(p).
- La trace d'une rotation plane d'angle θ est donnée par : Tr(Rθ) = 2cosθ.
- Plus généralement pour tout entier
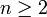 , la trace d'une rotation d'axe Δ et d'angle θ dans l'espace à n dimensions est donnée par : Tr(RΔ,θ) = n − 2 + 2cosθ.
, la trace d'une rotation d'axe Δ et d'angle θ dans l'espace à n dimensions est donnée par : Tr(RΔ,θ) = n − 2 + 2cosθ. - La trace de la matrice d'adjacence d'un graphe est nulle (si un sommet ne boucle pas sur lui-même).
Notes et références
- Portail des mathématiques
Catégorie : Application linéaire
Wikimedia Foundation. 2010.