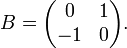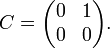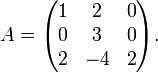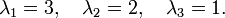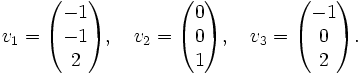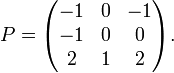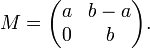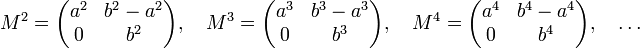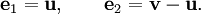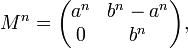- Matrice Diagonalisable
-
Matrice diagonalisable
En algèbre linéaire, une matrice carrée M d'ordre n (
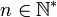 ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c'est-à-dire s'il existe une matrice inversible P et une matrice diagonale D telles que PDP − 1 = M.
) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c'est-à-dire s'il existe une matrice inversible P et une matrice diagonale D telles que PDP − 1 = M.Par exemple, toute matrice diagonale est diagonalisable, il suffit de prendre P = In (où In est la matrice identité) dans la définition. Ainsi la matrice nulle est diagonalisable, la matrice identité, les matrices scalaires, ...
Rappelons que si E est un espace vectoriel de dimension finie, alors un endomorphisme f de E est diagonalisable lorsqu'il existe une base de E telle que la matrice de f relativement à cette base soit diagonale.
Notons can(M), l'endormorphisme de Kn canoniquement associé à la matrice M, c'est-à-dire l'application linéaire de Kn dans Kn qui a pour matrice relativement à la base canonique de Kn, la matrice M.
Le concept de changement de base permet de démontrer que la matrice M est diagonalisable si et seulement si can(M) est diagonalisable.
La diagonalisation d'une matrice se ramène donc à la diagonalisation d'un endomorphisme d'un espace vectoriel de dimension finie et réciproquement.
La diagonalisation des matrices (ou des endomorphismes) est intéressante parce que les matrices diagonales sont très faciles à manipuler :
- leurs valeurs propres et vecteurs propres se déterminent aisément,
- on les élève à des puissances entières en élevant tout simplement leurs coefficients diagonaux à cette puissance, ce qui permet d'en déduire les puissances d'une matrice diagonalisable. Ces puissances représentent le résultat d'applications successives de cette matrice, et sont utiles pour simuler des itérations en analyse numérique. (voir Varga, Matrix Iterative Analysis)
K étant un corps commutatif, nous noterons dans tout l'article
 l'espace vectoriel des matrices carrées d'ordre n, et
l'espace vectoriel des matrices carrées d'ordre n, et 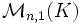 l'espace vectoriel des matrices à n lignes et une colonne. En diagonalisant une matrice, on se place dans une base où l'on travaille avec une matrice diagonale, ce que simplifie énormément les calculs. Et en général une réduction d'endomorphisme permet de simplifier les calculs. On peut donc faire appel à cette méthode pour les problèmes de résolution de systèmes d'équations linéaires par exemple.
l'espace vectoriel des matrices à n lignes et une colonne. En diagonalisant une matrice, on se place dans une base où l'on travaille avec une matrice diagonale, ce que simplifie énormément les calculs. Et en général une réduction d'endomorphisme permet de simplifier les calculs. On peut donc faire appel à cette méthode pour les problèmes de résolution de systèmes d'équations linéaires par exemple.Sommaire
Diagonalisation des matrices
Définitions
Article détaillé : Valeur propre.Définition 1 — Soit
 et soit
et soit 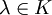 . Le scalaire λ est appelé valeur propre de M, s'il existe un vecteur colonne X non nul de
. Le scalaire λ est appelé valeur propre de M, s'il existe un vecteur colonne X non nul de 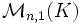 telle que MX = λX.
telle que MX = λX.L'ensemble des valeurs propres d'une matrice M s'appelle le spectre de M et est noté généralement Sp(M) ou Spec(M).
Remarque: Il est important de préciser que le vecteur colonne X doit être non nul, sinon tout scalaire de K serait valeur propre de M puisqu'on a toujours M0 = λ0!
Définition 2 — Soit
 . Un vecteur X non nul de
. Un vecteur X non nul de 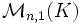 est appelé vecteur colonne propre ou colonne propre si et seulement s'il existe
est appelé vecteur colonne propre ou colonne propre si et seulement s'il existe 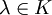 tel que MX = λX.
tel que MX = λX.On dit alors que X est une colonne propre associée à la valeur propre λ.
Remarque: La condition dans la définition
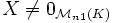 , a pour conséquence qu'un vecteur propre possède une unique valeur propre. Cette condition n'est pas toujours utilisée dans la définition. C'est néanmoins la convention utilisée dans Wikipedia.
, a pour conséquence qu'un vecteur propre possède une unique valeur propre. Cette condition n'est pas toujours utilisée dans la définition. C'est néanmoins la convention utilisée dans Wikipedia.Définition 3 — Soit
 et soit
et soit 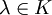 une valeur propre de M. Le sous-espace propre associé à la valeur propre λ est le noyau de l'endomorphisme
une valeur propre de M. Le sous-espace propre associé à la valeur propre λ est le noyau de l'endomorphisme 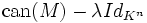 . Il est habituellement noté Eλ.
. Il est habituellement noté Eλ.Mais il est quelquefois défini comme étant le noyau de la matrice M − λIn (In étant la matrice unité d'ordre In), c'est-à-dire l'ensemble:
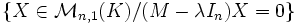 ,
,
aussi égal à
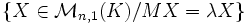 .
.
Ces définitions correspondent exactement à celles données dans le monde des endomorphismes (cf Valeur propre).
Recherche des valeurs propres
Théorème — Considérons une matrice M d'ordre n à coefficients dans un corps commutatif K et
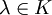 . Les propositions suivantes sont équivalentes:
. Les propositions suivantes sont équivalentes:- λ est valeur propre de M (
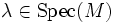 ),
), - M − λIn non inversible,
- le système (M − λIn)X = 0 d'inconnue
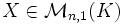 admet au moins une solution non nulle,
admet au moins une solution non nulle, 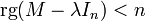 ,
,- det(M − λIn) = 0 (det désigne le déterminant d'une matrice).
De ce théorème se déduisent différentes techniques de recherche des valeurs propres. Étant donné un scalaire λ de K, il est possible de déterminer si M − λIn est inversible ou le rang de M − λIn en réduisant la matrice par la méthode de Gauss. Cette réduction s'effectue en choisissant si possible, un pivot indépendant de λ afin d'éviter les distinctions de cas.
Il est parfois plus efficace, lorsque la matrice M − λIn comporte « beaucoup de zéros », de résoudre le système (M − λIn)X = 0 dans lequel λ est considéré comme paramètre, en recherchant les solutions non nulles, ce qui a l'avantage de donner en même temps les vecteurs colonnes propres.
Enfin le calcul du déterminant de M − λIn peut donner les valeurs propres. Cela revient à déterminer les racines du polynôme caractéristique.
D'autre part, les valeurs propres d'une matrice M, peuvent être obtenues à partir d'un polynôme annulateur P, c'est-à-dire tel que P(A) = 0. Si λ est une valeur propre de M alors λ est racine du polynôme P. La réciproque n'étant pas vraie, il faut déterminer les racines de P pour lesquelles M − λIn n'est pas inversible. Par exemple, si A est une matrice d'un projecteur, alors A2 = A donc le polynôme P(X) = X2 − X est annulateur de A. Les valeurs propres possibles de A sont alors 0 et 1. Mais le projecteur nul, n'admet que 0 comme valeur propre.
Les méthodes de recherche des valeurs propres débouchent sur la détermination de racines de polynômes, ce qui pose généralement des problèmes dans le cas où l'ordre de la matrice est supérieur à 5 à cause de l'absence de formule générale donnant les racines en fonction des coefficients.
Donnons maintenant quelques moyens de détection d'erreurs dans la recherche des valeurs propres.
- Nous savons que les sous-espaces propres associés aux différentes valeurs propres d'une matrice M d'ordre n sont en somme directe et donc la somme des dimensions reste inférieure à la dimension de Kn. Ainsi une matrice M d'ordre n ne peut admettre plus de n valeurs propres distinctes.
- La trace d'une matrice M est un invariant de similitude c'est-à-dire que pour toute matrice inversible P, tr(P − 1MP) = trM. Donc la trace d'une matrice M est égale à la somme de ses valeurs propres (comptées avec leur multiplicité). Ainsi lorsqu'une matrice d'ordre n admet n valeurs propres distinctes, la trace constitue une sorte de somme de contrôle.
Recherche des vecteurs colonnes propres
Les colonnes propres associées à une valeur propre λ peuvent être obtenues en résolvant le système (M − λIn)X = 0, mais la connaissance de la dimension du sous-espace propre associé peut aider à les obtenir plus facilement. Par exemple si on sait qu'il y a n valeurs propres distinctes, alors la dimension des sous-espaces propres est égale à un, et il suffit de trouver une seule colonne non nulle solution du système (M − λIn)X = 0, les autres lui seront proportionnelles. Si les valeurs propres ont été déterminées en réduisant M − λIn par la méthode de Gauss, alors le nombre de pivots donne le rang de la matrice et d'après le théorème du rang, la dimension du sous-espace propre associé est égale à n − rg(M − λIn).
Méthodes pratiques de diagonalisation
- Dans la plupart des cas, il est nécessaire de calculer le polynôme caractéristique de la matrice, afin de déterminer ses valeurs propres et les sous-espaces propres associés :
Pour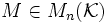 le polynôme caractéristique est
le polynôme caractéristique est 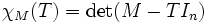 où T est l'indéterminée et
où T est l'indéterminée et 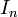 est la matrice unité de
est la matrice unité de 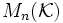 .
.
Les valeurs propres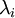 sont les racines de
sont les racines de 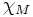 , il y a donc au plus
, il y a donc au plus 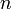 valeurs propres de multiplicité
valeurs propres de multiplicité 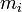 .
.
On calcule ensuite les sous-espace propres associés à chaque valeur propre:
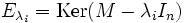
La matrice ne sera diagonalisable que si la dimension de chaque sous-espace propre est égale à la multiplicité
est égale à la multiplicité 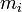 de la valeur propre
de la valeur propre 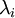 , ce qui signifie que pour chaque
, ce qui signifie que pour chaque 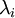 on a une base de
on a une base de 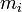 vecteurs propres que l'on note
vecteurs propres que l'on note 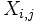 ,
, 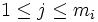 .
.
Alors il existera une matrice inversible U telle que U − 1MU soit égale à une matrice diagonale dont les coefficients diagonaux sont les
dont les coefficients diagonaux sont les 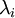 répétés
répétés 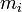 fois et
fois et 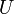 sera la matrice dont les colonnes sont les vecteurs
sera la matrice dont les colonnes sont les vecteurs 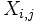 (l'ordre n'a pas d'importance, mais si on a le vecteur
(l'ordre n'a pas d'importance, mais si on a le vecteur 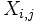 sur la k-ième colonne de
sur la k-ième colonne de 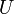 , alors on a la valeur propre
, alors on a la valeur propre 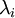 sur la k-ième colonne de
sur la k-ième colonne de  ).
). - Il est aussi possible de déterminer directement les valeurs propres, et des bases des sous-espaces propres associés. La matrice M est diagonalisable si et seulement si la somme des dimensions des différents sous-espaces propres est égale n. Si la matrice est diagonalisable, alors il existe une matrice inversible P obtenue en plaçant les unes à côté des autres, les colonnes propres formant une base de chacun des sous-espaces, et la matrice D = P − 1MP est alors diagonale. La dimension du sous-espace propre associé à une valeur propre, correspond au nombre de fois que celle-ci est répétée sur la diagonale de la matrice diagonale D semblable à la matrice M.
Propriétés
Les résultats fondamentaux sur la diagonalisation des matrices sont les suivants:
- Une matrice A d'ordre n sur un corps commutatif K est diagonalisable si et seulement si la somme des dimensions de ses sous-espaces propres est égale à n, et si et seulement s'il existe une base de
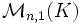 constituée de vecteurs colonnes propres de A. Si une telle base existe, alors il est possible de former la matrice P ayant comme colonnes ces colonnes propres, P est inversible et P − 1AP sera alors une matrice diagonale. Les coefficients diagonaux de cette matrice ne sont autres que les valeurs propres de A.
constituée de vecteurs colonnes propres de A. Si une telle base existe, alors il est possible de former la matrice P ayant comme colonnes ces colonnes propres, P est inversible et P − 1AP sera alors une matrice diagonale. Les coefficients diagonaux de cette matrice ne sont autres que les valeurs propres de A. - Une matrice peut être diagonalisable sur un corps commutatif K si son polynôme minimal est scindé et que toutes ses racines sont simples, c'est-à-dire s'il est produit de polynômes à coefficients dans K du premier degré distincts. Ce n'est cependant pas une condition nécessaire.
Le résultat suivant, suffisant mais pas nécessaire, est souvent utile:
Une matrice A d'ordre n est diagonalisable sur le corps K si elle a n valeurs propres distinctes dans K, c'est-à-dire si son polynôme minimal a n racines distinctes dans K.
En général, sur
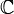 presque toutes les matrices sont diagonalisables. Plus précisément: l'ensemble des matrices complexes d'ordre n qui ne sont pas diagonalisables, considéré comme un sous-ensemble de
presque toutes les matrices sont diagonalisables. Plus précisément: l'ensemble des matrices complexes d'ordre n qui ne sont pas diagonalisables, considéré comme un sous-ensemble de  , est un ensemble de mesure nulle pour la mesure de Lebesgue. On peut également signaler que les matrices diagonalisables forment un sous-ensemble dense dans l'ensemble des matrices pour la topologie donnée par n'importe quelle norme matricielle.
, est un ensemble de mesure nulle pour la mesure de Lebesgue. On peut également signaler que les matrices diagonalisables forment un sous-ensemble dense dans l'ensemble des matrices pour la topologie donnée par n'importe quelle norme matricielle.Le résultat ne tient pas sur
 . À mesure que n augmente, il devient (dans un certain sens) de moins en moins probable qu'une matrice réelle d'ordre n, aléatoirement choisie, soit diagonalisable sur
. À mesure que n augmente, il devient (dans un certain sens) de moins en moins probable qu'une matrice réelle d'ordre n, aléatoirement choisie, soit diagonalisable sur  .
.Exemples
Exemple 1
Matrices non diagonalisables:
Certaines matrices réelles ne sont pas diagonalisables sur le corps des réels. Considérons par exemple la matrice
La matrice B n'a pas de valeurs propres réelles, ainsi il ne peut exister de matrice réelle Q inversible telle que Q − 1BQ soit une matrice diagonale. Mais, il est possible de diagonaliser B sur le corps des complexes. En prenant,
Alors Q − 1BQ est diagonale.
Cependant, il existe aussi des matrices non diagonalisables, même si le corps des complexes est utilisé. Cela se produit si les multiplicités algébriques et géométriques des valeurs propres ne coïncident pas. Par exemple, considérons:
La matrice n'est pas diagonalisable: il n'existe pas de matrice U inversible telle que U − 1CU soit diagonale. En effet, C a une valeur propre (qui est 0) et cette valeur propre a un ordre de multiplicité algébrique égal à 2 et géométrique égal à 1.
Exemple 2
Considérons la matrice:
Cette matrice admet comme valeurs propres:
Ainsi A qui est de rang 3, a 3 valeurs propres distinctes, donc est diagonalisable.
Si nous voulons diagonaliser A, nous avons besoin de déterminer les vecteurs propres correspondants. Il y a par exemple:
On vérifie facilement que Avk = λkvk.
Maintenant soit P la matrice ayant ces vecteurs propres comme colonnes:
Alors « P diagonalise A », comme le montre un simple calcul:
Remarquez que les valeurs propres λk apparaîssent sur la diagonale de la matrice dans le même ordre que nous avons placé les colonnes propres pour former P.
Exemple 3
Soit

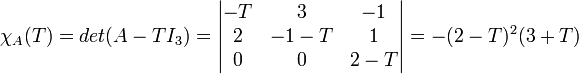 (voir le calcul d'un déterminant)
(voir le calcul d'un déterminant)
Donc les valeurs propres sont :- 2 de multiplicité 2
- -3 de multiplicité 1
Calcul des sous-espaces caractéristiques :
Calcul de E2 : On cherche les tels que :
tels que :

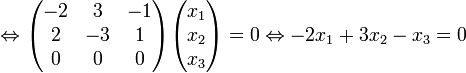
Donc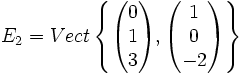
On procède de même pour et on obtient :
et on obtient :
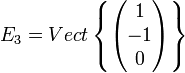
On a bien :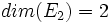 et
et  , donc cette matrice est diagonalisable.
, donc cette matrice est diagonalisable.
Une diagonalisation possible est :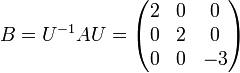 , avec
, avec 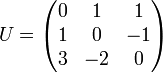
Les applications
Puissances de matrices
La diagonalisation peut être utilisée pour calculer efficacement les puissances d'une matrice diagonalisable A. Supposons que nous ayons obtenu:
- P − 1AP = D
où D est une matrice diagonale. Alors
- Ak = (PDP − 1)k = PDkP − 1
et cette dernière puissance est facile à calculer puisque la puissance kème d'une matrice diagonale s'obtient en élevant les coefficients diagonaux à la puissance k.
Par exemple considérons la matrice suivante:
En calculant les différentes puissances de M nous obtenons les formes suivantes:
Ce phénomène peut être expliqué en diagonalisant M. Pour ce faire, nous avons besoin d'une base de
 formée de vecteurs colonnes propres de M. Une telle base de colonnes propres est donnée par:
formée de vecteurs colonnes propres de M. Une telle base de colonnes propres est donnée par:où les ei désignent les vecteurs de la base canonique de
 .
.L'inverse de la matrice de passage peut s'obtenir à partir de
Un calcul direct montre que
Ainsi, a et b sont les valeurs propres associées à u et v, repsectivement. D'après la linéairité de la multiplication par une matrice, nous avons donc
En revenant à la base canonique, nous avons:
Les relations précédentes, exprimées sous forme matricielle donnent:
ce qui explique le phénomène précédent.
Systèmes Récurrents
Systèmes Différentiels
Équations Différentielles du nième ordre
Voir aussi
- Portail des mathématiques
Catégorie : Matrice
Wikimedia Foundation. 2010.