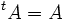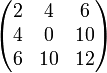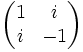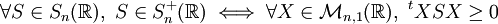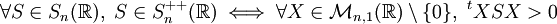- Matrice Symétrique
-
Matrice symétrique
Sommaire
Définitions
- En algèbre linéaire, une matrice symétrique est une matrice qui est égale à sa propre transposée. Ainsi A est symétrique si :
ce qui exige que A soit une matrice carrée.
Intuitivement, les coefficients d'une matrice symétrique sont symétriques par rapport à la diagonale principale (du coin en haut à gauche jusqu'à celui en bas à droite).
Exemple :
- L'ensemble des matrices symétriques à coefficients dans un anneau K est noté Sn(K).
- Toute matrice diagonale est symétrique, puisque tous les coefficients en dehors de la diagonale principale sont nuls.
- Un théorème fondamental concernant de telles matrices est le théorème spectral en dimension finie, qui énonce que les matrices symétriques dont les coefficients sont des nombres réels sont diagonalisables à l'aide de matrices orthogonales.
- Remarque : il existe des matrices symétriques non diagonalisables à coefficients complexes. Exemple :
En effet, cette matrice admet 0 comme seule valeur propre ; si elle était diagonalisable, elle serait nulle.
Interprétations
- En algèbre bilinéaire, une matrice représentant une forme bilinéaire est symétrique ssi cette dernière est symétrique.
- Dans un espace euclidien, une matrice représentant un endomorphisme dans une base orthonormée est symétrique ssi l'endomorphisme est auto-adjoint.
Matrices symétriques positives
Définitions
- Une matrice symétrique réelle est positive si et seulement si elle représente une forme bilinéaire positive.
- L'ensemble des matrices symétriques positives d'ordre n est noté
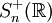
- Autrement dit :
- L'ensemble des matrices symétriques positives d'ordre n est noté
- Une matrice symétrique réelle est définie positive si et seulement si elle représente une forme bilinéaire définie positive.
- L'ensemble des matrices symétriques définies positives d'ordre n est noté
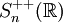
- En clair,
- L'ensemble des matrices symétriques définies positives d'ordre n est noté
Propriétés
- Une matrice symétrique est positive si et seulement si ses valeurs propres (qui sont automatiquement réelles) sont positives.
- Une matrice symétrique est définie positive si et seulement si ses valeurs propres sont strictement positives.
- Pour toute matrice réelle A, la matrice tAA est une matrice symétrique positive. De plus si A est une matrice carrée inversible, tAA est définie positive.
- Toute matrice symétrique positive admet une unique racine carrée symétrique positive, en clair :
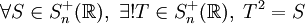 .
.
Ce résultat se généralise aux racines n-ièmes.
Utilisations concrètes
- Une matrice symétrique d'ordre 3 représente une conique en coordonnées homogènes dans un plan projectif construit à partir de
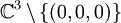 .
.
Voir aussi
- Portail des mathématiques
Catégorie : Matrice remarquable
Wikimedia Foundation. 2010.