- Matrice trigonalisable
-
Trigonalisation
En algèbre linéaire, trigonaliser une matrice consiste à réduire celle-ci sous la forme d'une matrice triangulaire supérieure, ou inférieure. Ceci n'est possible que sous certaines conditions.
Dans la suite, on se donne
 un entier naturel et
un entier naturel et 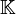 un corps commutatif.
un corps commutatif. 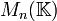 désignera l'ensemble des matrices à n lignes et n colonnes à coefficients dans
désignera l'ensemble des matrices à n lignes et n colonnes à coefficients dans 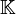 .
.Sommaire
Matrices triangulaires
Article détaillé : matrice triangulaire.Une matrice triangulaire supérieure est une matrice dont tous les coefficients situés strictement en dessous de la diagonale sont nuls. En général, on note
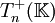 l'ensemble des matrices triangulaires supérieures. C'est un espace vectoriel, et même mieux, c'est une sous-algèbre de
l'ensemble des matrices triangulaires supérieures. C'est un espace vectoriel, et même mieux, c'est une sous-algèbre de 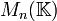 . Une matrice triangulaire supérieure T est donc de la forme :
. Une matrice triangulaire supérieure T est donc de la forme :Remarque : De la même manière, une matrice triangulaire inférieure est une matrice dont tous les coefficients situés strictement au dessus de la diagonale sont nuls.
Endomorphismes et matrices trigonalisables
Soit
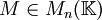 , une matrice à n lignes et n colonnes à coefficients dans
, une matrice à n lignes et n colonnes à coefficients dans 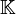 . On dit que la matrice M est trigonalisable s'il existe une matrice inversible
. On dit que la matrice M est trigonalisable s'il existe une matrice inversible 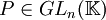 et une matrice
et une matrice 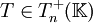 triangulaire supérieure telles que :
triangulaire supérieure telles que :- M = PTP − 1 ou bien T = P − 1MP
Cela revient à dire que M est semblable dans
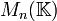 à une matrice triangulaire supérieure.
à une matrice triangulaire supérieure.En particulier, toute matrice triangulaire supérieure est trigonalisable, bien évidemment. (Il suffit de choisir P = In où In est la matrice identité de dimension n.)
Soit E un espace vectoriel sur le corps
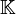 , de dimension n et u un endomorphisme de E. On dit que u est trigonalisable s'il existe une base
, de dimension n et u un endomorphisme de E. On dit que u est trigonalisable s'il existe une base  de E telle que
de E telle que  , où
, où  désigne la matrice de l'endomorphisme u dans la base
désigne la matrice de l'endomorphisme u dans la base  . Autrement dit, un endomorphisme est trigonalisable s'il existe une base dans laquelle sa matrice associée est triangulaire supérieure.
. Autrement dit, un endomorphisme est trigonalisable s'il existe une base dans laquelle sa matrice associée est triangulaire supérieure.De plus, un endomorphisme est trigonalisable si et seulement si sa matrice dans au moins une base de E est trigonalisable ; dans ce cas, sa matrice dans n'importe quelle base de E est trigonalisable.
Il faut noter un théorème important dû à Schur :
Théorème de trigonalisation de Schur — Toute matrice carrée complexe est trigonalisable dans une base orthonormale.
Conditions de trigonalisation
Il existe plusieurs critères pour savoir si une matrice ou un endomorphisme sont trigonalisables :
- Toute matrice diagonalisable est a fortiori trigonalisable (car une matrice diagonale est un cas particulier de matrice triangulaire).
- Une matrice est trigonalisable si et seulement si son polynôme caractéristique est scindé dans
![\mathbb{K} [X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) .
.
- En particulier, si
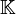 est algébriquement clos, toute matrice de
est algébriquement clos, toute matrice de 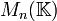 est trigonalisable. Cet énoncé est aussi valable pour un endomorphisme de E, espace vectoriel de dimension n sur
est trigonalisable. Cet énoncé est aussi valable pour un endomorphisme de E, espace vectoriel de dimension n sur 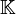 .
. - Cas particulier où
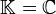 : toute matrice de
: toute matrice de  est trigonalisable, car
est trigonalisable, car 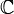 est algébriquement clos (voir théorème de d'Alembert-Gauss).
est algébriquement clos (voir théorème de d'Alembert-Gauss).
- Un endomorphisme est trigonalisable s'il existe un drapeau de E stable par cet endomorphisme.
Exemples de trigonalisation
Matrices carrées d'ordre 2 à coefficients réels
Soit
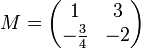 une matrice, son polynôme caractéristique est
une matrice, son polynôme caractéristique est 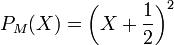 qui a comme unique racine
qui a comme unique racine 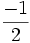 qui est donc l'unique valeur propre de M. L'espace propre associé à la valeur propre
qui est donc l'unique valeur propre de M. L'espace propre associé à la valeur propre 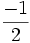 est
est 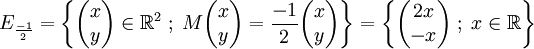 ,
,  est donc un sous espace vectoriel de dimension 1 qui a pour base le vecteur
est donc un sous espace vectoriel de dimension 1 qui a pour base le vecteur 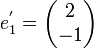 . On peut alors compléter
. On peut alors compléter  avec par exemple le vecteur
avec par exemple le vecteur  de manière à ce que
de manière à ce que  forme une base de l'espace
forme une base de l'espace  tout entier. On sait déjà que
tout entier. On sait déjà que 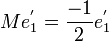 et on a facilement
et on a facilement 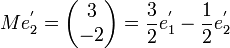 , la matrice M dans la base
, la matrice M dans la base 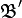 s'écrit donc
s'écrit donc 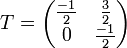 . On remarquera que la dimension de l'espace propre ne permettait pas ici de diagonaliser la matrice M. La matrice P telle que M = PTP − 1 n'est autre que la matrice de passage de la base canonique
. On remarquera que la dimension de l'espace propre ne permettait pas ici de diagonaliser la matrice M. La matrice P telle que M = PTP − 1 n'est autre que la matrice de passage de la base canonique 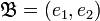 à la base
à la base 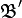 , P est donc constituée des vecteurs de
, P est donc constituée des vecteurs de 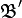 exprimés dans la base
exprimés dans la base 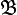 donc
donc 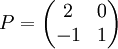 . De même, pour avoir la matrice P − 1 il suffit d'exprimer les vecteurs de
. De même, pour avoir la matrice P − 1 il suffit d'exprimer les vecteurs de 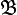 dans la base
dans la base 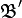 , on a facilement
, on a facilement 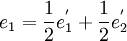 et
et 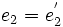 et donc
et donc 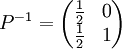 .
.Exemple de trigonalisation d'une matrice carrée d'ordre 3
Soit
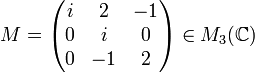 son polynôme caractéristique est
son polynôme caractéristique est 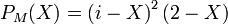 . Comme dans l'exemple précédent on a après calculs :
. Comme dans l'exemple précédent on a après calculs : 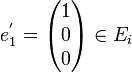 et
et 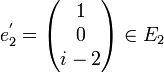 que l'on complète avec
que l'on complète avec 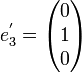 pour former une base
pour former une base 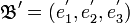 de
de 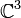 . On remarque que
. On remarque que 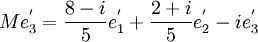 . La matrice M dans la base
. La matrice M dans la base 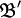 est donc
est donc 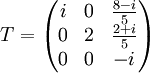 et l'on a M = PTP − 1 avec P la matrice de passage de la base canonique
et l'on a M = PTP − 1 avec P la matrice de passage de la base canonique 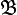 à la base
à la base 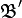 , P est donc constituée des vecteurs de
, P est donc constituée des vecteurs de 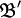 exprimés dans la base
exprimés dans la base 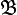 d'où
d'où 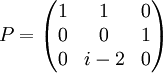 et
et  .
.Voir aussi
- Portail des mathématiques
Catégorie : Matrice
Wikimedia Foundation. 2010.

