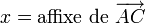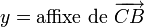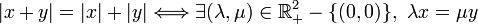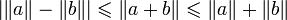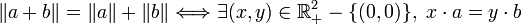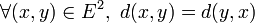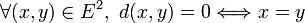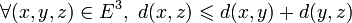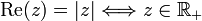- Inegalite triangulaire
-
Inégalité triangulaire
En mathématiques, l'inégalité triangulaire exprime en substance que le chemin direct est le plus court. Cette inégalité peut être énoncée sous la forme d'une propriété ou bien d'une condition nécessaire à la bonne définition d'une distance.
Sommaire
Enoncés
En géométrie
Dans un plan euclidien, soit un triangle ABC. Alors les longueur AB, AC et CB vérifient l'inégalité :
Deux propriétés complètent cette inégalité :
Pour les nombres complexes
En utilisant une représentation complexe du plan euclidien, on peut noter
On obtient cette formulation équivalente.
Pour
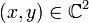 , on a :
, on a :Généralisation aux espaces préhilbertiens
Soit
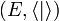 un espace préhilbertien. On note
un espace préhilbertien. On note  la norme quadratique associée au produit scalaire. Pour
la norme quadratique associée au produit scalaire. Pour 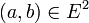 , on vérifie alors :
, on vérifie alors :Point de vue axiomatique
Voir Distance (mathématiques) pour un article plus détaillé sur la notion de distance en mathématiques.
Soit E un ensemble et
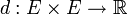 . On dit que d est une distance sur E si :
. On dit que d est une distance sur E si :La troisième propriété demandée à d pour être une distance est de vérifier l'inégalité triangulaire.
Démonstrations
Lemme
Enoncé
Pour
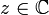 :
:Démonstration
Soient
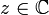 et
et 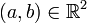 tels que z = a + ib.
tels que z = a + ib.Premièrement,
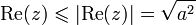 .
.Ensuite,
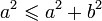 , car
, car 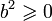 Par croissance de
Par croissance de 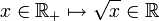 , on obtient
, on obtient 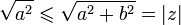 .
.Finalement
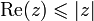 .
.Il y a égalité si Re(z) = | Re(z) | , c'est-à-dire si a est positif, et si | Re(z) | 2 = | z | 2, c'est-à-dire si b = 0.
Dans le cadre des nombres complexes
Soit
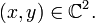
Inégalités
Or
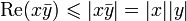 , par le lemme.
, par le lemme.Donc
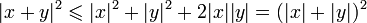
Par croissance de
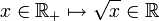 , on obtient
, on obtient 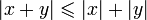 .
.
Posons x' = − x et y' = x + y.Par ce qui précède, on a
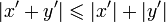 , c'est-à-dire
, c'est-à-dire 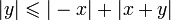 .
.Donc
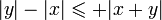
De même,
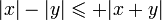
Finalement,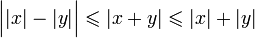
Cas d'égalité
Supposons que | x + y | = | x | + | y | .
On a alors
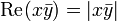 . Par le lemme,
. Par le lemme, 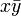 est un réel positif. C'est-à-dire que x et y ont même argument.
est un réel positif. C'est-à-dire que x et y ont même argument.Donc
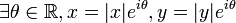 .
.
Finalement, on a bien λx = μy, avec λ = | y | et μ = | x | m.Dans le cadre d'un plan euclidien
La démonstration la plus rapide est d'utiliser une réprésentation complexe du plan euclidien et d'appliquer le résultat précédemment démontré.
Dans le cadre des espaces préhilbertiens
La démonstration a exactement la même structure que pour les complexes.
Soit
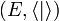 un espace préhilbertien. Soit
un espace préhilbertien. Soit 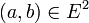 .
.Inégalités
On a
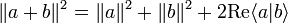 .
.
Par le lemme,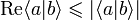 .
.Par l'inégalité de Cauchy-Schwarz,
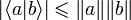 .
.D'où
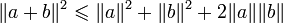 .
.Et donc
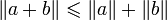
Posons a' = − a et b' = b + a. On a, par ce qui précède,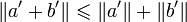 .
.C'est-à-dire, comme
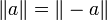 , on a
, on a 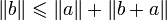 .
.En faisant de même en intervertissant a et b, on obtient
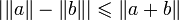 .
.
Finalement,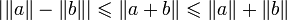
Cas d'égalité
Supposons que
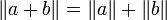 , et que
, et que 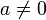 .
.Par ce qui précède, on a donc
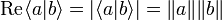 .
.Donc, par le cas d'égalité de Cauchy-Schwarz,
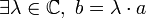 .
.Et
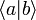 est un réel positif. Comme,
est un réel positif. Comme, 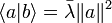 , λ est aussi un réel positif.
, λ est aussi un réel positif.
Finalement,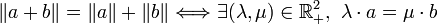
Articles connexes
- Portail de la géométrie
Catégories : Distance et longueur | Inégalité | Géométrie du triangle
Wikimedia Foundation. 2010.


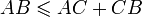
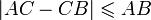
![AB = AC + CB \Leftrightarrow C \in [AB]](/pictures/frwiki/98/b0998e2695cd70b9795e6baf16695461.png)