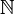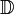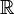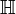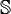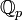- Nombres algébriques
-
Nombre algébrique
Un nombre algébrique, en mathématiques, est tout nombre qui est solution d'une équation algébrique (autrement dit racine d'un polynôme différent de zéro) à coefficients entiers (ou de manière équivalente, à coefficients rationnels). Sans plus de précision, on suppose qu'un nombre algébrique est un nombre complexe, mais on peut aussi considérer les nombres algébriques dans d'autres corps, tel que le corps des nombres p-adiques. Les éléments d'un corps de nombres sont (par définition) des nombres algébriques.
Le polynôme irréductible unitaire ayant un tel nombre pour racine est appelé polynôme minimal de ce nombre. L'étude de ces nombres, de leurs polynômes minimaux et des corps qui les contiennent est l'objet de la théorie de Galois.
Sommaire
Exemples
- Tout nombre rationnel est algébrique, car le quotient
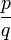 de deux entiers est racine de l'équation
de deux entiers est racine de l'équation 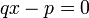 .
. - Un nombre irrationnel peut être ou non algébrique. Par exemple
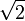 ou
ou 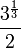 sont algébriques, car ils sont les solutions de
sont algébriques, car ils sont les solutions de 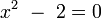 et
et 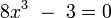 , respectivement.
, respectivement. - Le nombre complexe
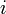 est algébrique, car il est racine de l'équation x2 + 1 = 0.
est algébrique, car il est racine de l'équation x2 + 1 = 0.
Propriétés
Les nombres qui ne sont pas algébriques sont appelés nombres transcendants. Presque tous les nombres complexes sont transcendants, parce que l'ensemble des nombres algébriques est dénombrable tandis que l'ensemble des nombres complexes, et par conséquent aussi l'ensemble des nombres transcendants, ne l'est pas. Les exemples les plus connus de nombres transcendants sont
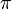 et
et  . D'autres exemples sont fournis par le théorème de Gelfond-Schneider.
. D'autres exemples sont fournis par le théorème de Gelfond-Schneider.Tous les nombres algébriques sont calculables et par conséquent sont définissables.
Si un nombre algébrique est racine d'une équation polynômiale de degré n, et s'il n'est racine d'aucune équation polynômiale de degré strictement inférieur à n, on dit que c'est un nombre algébrique de degré n. Par exemple, les nombres algébriques de degré 1 sont les rationnels ; i et
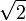 sont algébriques de degré 2.
sont algébriques de degré 2.Le concept de nombre algébrique peut être généralisé à des extensions de corps arbitraires; les éléments dans de telles extensions qui satisfont aux équations polynômiales sont appelés des éléments algébriques.
Le corps des nombres algébriques
La somme, la différence, le produit et le quotient de deux nombres algébriques sont encore algébriques (ce résultat n'est nullement évident ; la façon la plus simple de le démontrer passe par l'utilisation du résultant) ; par conséquent, les nombres algébriques forment un corps, habituellement noté
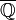 ; il est inclus dans
; il est inclus dans 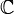 . On a
. On a 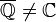 : en effet, il est connu que l'ensemble
: en effet, il est connu que l'ensemble 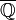 est dénombrable, alors que
est dénombrable, alors que 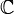 ne l'est pas. Il en résulte l'existence de nombres qui ne sont pas algébriques : on dit qu'ils sont transcendants. On peut montrer que chaque racine d'une équation polynômiale dont les coefficients sont des nombres algébriques est encore algébrique. Ceci peut être reformulé en disant que le corps des nombres algébriques est algébriquement clos. En fait, c'est le plus petit corps algébriquement clos contenant les nombres rationnels, et il est par conséquent appelé clôture algébrique du corps
ne l'est pas. Il en résulte l'existence de nombres qui ne sont pas algébriques : on dit qu'ils sont transcendants. On peut montrer que chaque racine d'une équation polynômiale dont les coefficients sont des nombres algébriques est encore algébrique. Ceci peut être reformulé en disant que le corps des nombres algébriques est algébriquement clos. En fait, c'est le plus petit corps algébriquement clos contenant les nombres rationnels, et il est par conséquent appelé clôture algébrique du corps 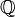 des rationnels.
des rationnels.Tous les énoncés ci-dessus sont très facilement démontrés dans le contexte général des éléments algébriques d'une extension de corps.
Nombres définis par des radicaux
Tous les nombres qui peuvent être obtenus à partir des entiers en utilisant un nombre fini d'additions, de soustractions, de multiplications, de divisions et d'extractions de racines n-ièmes (où n est un nombre entier positif) sont algébriques. La réciproque, néanmoins, n'est pas vraie : il existe des nombres algébriques qui ne peuvent pas être obtenus de cette manière (c'est le théorème d'Abel–Ruffini); d'après la théorie de Galois, tous ces nombres sont de degré supérieur ou égal à 5. Un exemple d'un tel nombre est l'unique racine réelle de
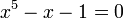 .Article détaillé : équation quintique.
.Article détaillé : équation quintique.Entiers algébriques
Article détaillé : entier algébrique.Un nombre algébrique qui satisfait une équation polynômiale de degré n à coefficients ai appartenant à l'ensemble
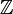 des entiers, dont le premier coefficient an vaut 1 (c'est-à-dire qui est racine d'un polynôme monique), est appelé un entier algébrique. Ainsi,
des entiers, dont le premier coefficient an vaut 1 (c'est-à-dire qui est racine d'un polynôme monique), est appelé un entier algébrique. Ainsi, 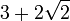 , racine de x2 − 6x + 1 et
, racine de x2 − 6x + 1 et 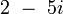 , racine de x2 − 4x + 29, sont des entiers algébriques ; il en est de même du nombre d'or
, racine de x2 − 4x + 29, sont des entiers algébriques ; il en est de même du nombre d'or 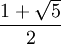 , qui est racine de x2 − x − 1 ; ce dernier exemple montre que les "coefficients" d'un entier algébrique peuvent ne pas être entiers ; cette question est développée dans l'article consacré aux entiers quadratiques.
, qui est racine de x2 − x − 1 ; ce dernier exemple montre que les "coefficients" d'un entier algébrique peuvent ne pas être entiers ; cette question est développée dans l'article consacré aux entiers quadratiques.La somme, la différence et le produit d'entiers algébriques sont encore des entiers algébriques, ce qui signifie que les entiers algébriques forment un anneau. Le nom entier algébrique provient du fait que les seuls nombres rationnels qui sont des entiers algébriques sont les entiers, et parce que les entiers algébriques dans tout corps de nombres sont sous bien des aspects analogues aux entiers. Si
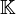 est un corps de nombres, son anneau d'entiers est le sous-anneau des entiers algébriques dans
est un corps de nombres, son anneau d'entiers est le sous-anneau des entiers algébriques dans 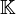 , et est fréquemment noté
, et est fréquemment noté 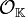 . Ces anneaux sont les exemples les plus typiques d'anneaux de Dedekind.
. Ces anneaux sont les exemples les plus typiques d'anneaux de Dedekind.Généralisation
Plus généralement : soient
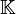 un corps, et
un corps, et 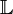 une extension de
une extension de 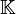 . Un élément de
. Un élément de 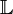 est dit algébrique sur
est dit algébrique sur 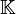 s'il est racine d'une équation polynomiale à coefficients dans
s'il est racine d'une équation polynomiale à coefficients dans 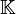 , non tous nuls ; il est dit transcendant sur
, non tous nuls ; il est dit transcendant sur 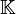 dans le cas contraire.
dans le cas contraire.La définition donnée plus haut s'obtient dans le cas particulier où
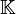 est le corps
est le corps 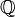 des rationnels et
des rationnels et 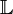 est le corps
est le corps 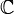 des nombres complexes.
des nombres complexes.Classes particulières de nombres algébriques
- Entier de Gauss
- Entier d'Eisenstein
- Entier de Dirichlet
- Entier quadratique
- Entier algébrique
- Racine de l'unité
- Période de Gauss
- Nombre de Pisot-Vijayaraghavan
- Nombre de Salem
Lien externe
- (histoire des sciences) L'article de 1874 de Cantor sur la dénombrabilité des nombres algébriques en ligne et commenté sur le site BibNum.
Voir aussi
- Portail des mathématiques
Catégories : Théorie algébrique des nombres | Type de nombre - Tout nombre rationnel est algébrique, car le quotient
Wikimedia Foundation. 2010.