- Algebre semi-simple
-
Algèbre semi-simple
En mathématiques et plus particulièrement en algèbre, une A-algèbre L, où A désigne un anneau, est qualifiée de semi-simple ou de complètement réductible si et seulement si la structure d'anneau associé à L l'est
Elle est présente dans de nombreuses branches mathématiques, on peut citer l'algèbre linéaire l'arithmétique, la théorie des représentations d'un groupe fini celle des groupes de Lie ou celle des algèbres de Lie. Elle est, par exemple, utilisée pour démontrer le critère de réciprocité de Frobenius.
La théorie des algèbres semi-simples, se fonde sur le lemme de Schur et le théorème d'Artin-Wedderburn.
Sommaire
Définitions
Tout au long de cet article, les notations suivantes sont utilisées : A désigne un anneau unitaire non nécessairement commutatif, L une algèbre unitaire sur l'anneau A. K désigne un corps, non nécessairement commutatif et E un espace vectoriel.
Plusieurs définitions sont nécessaire à la compréhension de la notion d'algèbre semi-simple. Les définitions diffèrent un peu du cas des module semi-simples. Par exemple un module est dit simple s'il n'admet pas d'autres sous-module que lui-même et l'ensemble nul. La situation archétypale de l'algèbre simple est celle de L(E), l'ensemble des endomorphismes de E. Il admet de nombreuses sous-algèbres, par exemple si p est un projecteur, alors l'ensemble des endomorphismes de la forme poa où a décrit les endomorphismes est une sous-algèbre, on utilise alors la définition suivante :
-
- L'algèbre L est dite simple si et seulement si les seuls idéaux bilatères sont l'ensemble nul et L lui-même.
K est une algèbre simple considéré comme un espace vectoriel sur lui-même. L'anneau des entiers Z n'est pas une Z-algèbre simple, en effet tout sous-module n.Z si n est un entier contient le sous-module 2.nZ. Cette définition se généralise aux modules, un module est dit simple s'il n'admet comme sous-module que lui-même et l'ensemble nul.
-
- Soit F un idéal de L, F est aussi appelé un facteur invariant.
Le corps des nombres complexes est une algèbre en tant qu'espace vectoriel réel, R l'ensemble des nombres réels est un sous-module simple mais n'est pas un facteur invariant au sens de l'algèbre. Si E est de dimension deux de base (e1, e2) et si L est la K algèbre des endomorphismes ayant la base comme vecteurs propres, alors le sous-ensemble de L ayant pour image de e1 le vecteur nul est un facteur invariant.
-
- Soit F un facteur invariant, F est dit facteur direct si et seulement s'il existe un supplémentaire invariant par F.
Avant de donner la définition d'une algèbre semi-simple rappelons qu'un module est dit semi-simple si et seulement s'il est somme directe de facteurs invariants. La notation suivante est utilisée dans l'article LL désigne le module L sur l'anneau L.
-
- Une algèbre L est dite semi-simple si et seulement si les modules LL à droite et à gauche le sont.
Cette définition induit immédiatement la définition d'un anneau semi-simple :
-
- Un anneau est dit semi-simple si et seulement s'il est semi-simple en tant qu'algèbre sur lui-même.
Histoire
Origines
L'histoire de l'étude de la notion d'algèbre est initialement étroitement liée à celui de la relation entre l'algèbre linéaire et la théorie des groupes. Arthur Cayley (1821-1895) développe en 1850 la notion de matrice[1]. Cette notion apporte de nombreux services dont l'un est à l'origine du concept. Elle permet d'incarner des groupes et particulièrement les groupes de Galois et de les étudier sous un axe nouveau, celui d'un groupe de matrices. À l'origine seul le cas fini est étudié, l'analyse met en évidence une nouvelle structure, que l'on considère maintenant comme l'algèbre des endomorphismes engendrés par les automorphismes du groupe.
Camille Jordan (1838-1922), le grand spécialiste de l'époque avec Cayley, l'utilise intensivement. En 1869, elle lui permet de démontrer l'existence[2] d'une chaîne de composition pour les groupes finis connue sous le nom de théorème de Jordan-Hölder. Le caractère d'unicité d'une telle chaîne est démontré par Otto Hölder (1859-1937) vingt ans plus tard. Ce théorème possède deux lectures possibles, l'une sur les groupes finis, l'autre sur les modules. La deuxième lecture correspond à une propriété structurelle essentielle, elle est une des origines de l'intérêt pour ce qui deviendra une branche des mathématiques, l'algèbre commutative. L'analyse du groupe de Galois offre des perspectives aussi en algèbre linéaire. Elle amène Jordan à étudier les endomorphismes en dimension finie à travers cette algèbre et permet une compréhension aussi profonde que définitive de leur structure. Ce résultat, est publié dans un livre de synthèse[3] en 1870. Il est connu sous le nom de réduction de Jordan et s'applique sur les corps finis premiers, c'est-à-dire les corps des entiers modulo un nombre premier.
Les conséquences des travaux de Jordan sont considérables, son livre de synthèse devient la référence sur les théories des groupes, de Galois et de l'algèbre linéaire. Il démontre d'une part que l'analyse des groupes à travers le groupe linéaire est une démarche féconde, et par ailleurs que la structure d'algèbre est riche en enseignements à la fois en termes de module et d'algèbre linéaire.
Théorie des groupes
La recherche de la compréhension des groupes devient un sujet majeur en mathématique. Par delà leur intérêt propre, la compréhension de cette structure est la clé de nombreux sujets. La théorie de Galois les place au cœur du problème de l'équation algébrique et les conséquences sont multiples, l'analyse des structures de corps s'identifie à cette époque à la théorie de Galois et la compréhension de nombreux anneaux, utiles en arithmétique s'appuie sur cette théorie. La géométrie ne fait rapidement plus exception. En 1870, deux mathématiciens Felix Klein (1849 1925) et Sophus Lie (1842 1899) visitent Jordan à Paris. Ils sont particulièrement intéressés par une de ses publications[4] vieille d'un an sur l'analyse d'une géométrie à l'aide d'un groupe de symétries. Sophus Lie développe une théorie des groupes continus et Klein, dans son fameux programme[5] classifie les géométries à travers les groupes. Ils perdent leur caractère essentiellement fini.
Georg Frobenius (1849-1917), à la suite d'une correspondance[6] avec Richard Dedekind (1831 1916) s'intéresse aux groupes finis et particulièrement à la notion de factorisation d'une représentation matricielle appelée à l'époque déterminant de groupe et maintenant tombé en désuétude. Ces lettres sont à l'origine de la théorie des représentations d'un groupe. En 1897 il saisit[7] la proximité entre une représentation c'est-à-dire un groupe qui opère linéairement sur un espace vectoriel et un module, où un anneau opère sur l'espace. Le saut est franchi, le groupe est linéarisé et devient un module. Tout progrès sur les modules ayant une structure équivalente à celle d'un module sur un groupe est sujet à faire progresser la théorie des représentation et donc celle des groupes.
Heinrich Maschke (1853 1908), un élève de Klein, est le premier à démontrer le théorème[8] qui détermine l'élément structurant de ce type de module, il est semi-simple. Il possède des analogies fortes avec les anneaux euclidiens comme celui des nombres entiers. Ils se décomposent en une série de modules simples qui correspondent un peu aux nombres premiers, à la différence qu'il n'en existe qu'un nombre fini.
Structure d'algèbre
Une structure apparaît de plus en plus centrale, celle d'algèbre semi-simple. Dans le cas des représentations, elle correspond à faire opérer l'extension linéaire du groupe, non plus sur un espace vectoriel quelconque, mais sur lui-même. D'autres branches mathématiques amènent naturellement à l'utilisation de ce concept. Une extension galoisienne dispose d'une structure analogue et la théorie des corps suppose l'étude de ces objets. Enfin, les groupes continus développés par Lie disposent en chaque point d'un espace tangent équipé d'une structure d'algèbre semi-simple. À l'aube du XXe siècle, ce sujet devient majeur, des mathématiciens d'horizon divers étudient ce concept. Le théorème de décomposition des modules s'appliquent car une algèbre dispose aussi d'une structure de module.
William Burnside (1852 1927) saisit rapidement la portée de l'approche de Frobenius. L'importance de la structure de l'algèbre sous-jacente à un groupe linéaire ne lui échappe pas. Il établit dès 1897 dans la première édition[9] de son livre de référence sur les groupe finis un premier résultat. Dans le cas où le corps est algébriquement clos l'ensemble des endomorphismes d'un espace vectoriel de dimension finie est une algèbre simple. Un exemple des briques élémentaires est alors explicité.
Leonard Dickson (1874-1954) écrit en 1896 sa thèse de doctorat à propos les groupes de Galois comme des groupes linéaires sur des corps finis quelconques, généralisant ainsi les résultats de Jordan. Il démontre que tout corps fini commutatif est une extension de Galois d'un corps premier. Elle est publiée[10] en Europe en 1901. La structure de base est celle d'une algèbre semi-simple. Si l'approche de Galois ne permet que l'étude des corps commutatifs, les algèbres semi-simples permettent aussi celui des corps gauches (ie. non commutatifs), Dickson développe la théorie général des corps et trouve de nombreux exemples de corps gauches. A partir de cette période les deux théories : celle de Galois et celle des corps commencent leur séparation.
Elie Cartan (1869-1951) s'intéresse dès sa thèse[11]qu'il soutient en 1894 aux algèbres de Lie. Toutes les structures d'algèbres simples et semi-simples sur les complexes y sont traitées. Avec Joseph Wedderburn (1882 - 1948), il étudie la structure générique de ces algèbres. Cartan explicite la structure des algèbres semi-simples pour le cas des nombres complexes. En 1907 Wedderburn publie son article[12] peut-être le plus célèbre. Il généralise les résultats de Cartan pour les algèbres sur un corps quelconque qu'on appelle à l'époque les nombres hypercomplexes. Cette généralisation est importante, car tous les exemples d'applications citées précédemment utilisent des corps gauches.
Structure d'anneau
Le théorème de Wedderburn modifie la situation, il existe des corps naturels pour toute algèbre simple, même si ces corps sont a priori non commutatifs. Le théorème doit donc pouvoir s'exprimer en termes d'anneau. Si Wedderburn ne le fait pas, en 1908 il propose néanmoins une classification comportant d'une part les anneaux à radicaux et d'autre part les semi-simples. Cette décomposition[13] devient la base de la théorie des anneaux pour le demi-siècle à venir.
Une grande figure de la recherche dans ce domaine est Emmy Noether (1882 - 1935). Elle est souvent considérée[14] comme la mère de la théorie moderne des anneaux. Elle développe la théorie des anneaux non commutatifs et fonde[15] une théorie générale des idéaux. Le concept d'idéal irréductible, correspondant à l'algèbre simple, est développée, ainsi que la théorie des anneaux dont toute chaîne ascendante strictement croissante d'idéaux est finie. Ces anneaux sont maintenant nommés en son honneur.
Emil Artin (1898 - 1962) étudie particulièrement un cas dont l'étude est initiée par Noether, celui des anneaux dont toute chaîne descendante strictement décroissante d'idéaux est finie. Un anneau semi-simple de longueur finie est à la fois artinien et noethérien. En 1927, Artin trouve[16] la forme définitive du théorème. Sans son formalisme linéaire, le théorème prend sa portée maximale, il devient un résultat important de l'algèbre non commutative. Une large classe d'anneaux, est isomorphe à un produit d'algèbres associative sur des corps quelconques.
Si le théorème est définitif, un de des attributs reste ouvert. Quelle classe d'anneaux autres que ceux à la fois artiniens et noethériens satisfont le théorème ? Un premier élément de réponse est apporté en 1939. C. Hopkins démontre[17] que, seule la condition sur la chaîne descendante est nécessaire. La véritable percée[18] est néanmoins l'œuvre de N. Jacobson, qui trouve la condition. Elle porte sur la notion de radical, maintenant essentielle pour l'étude des anneaux semi-simples.
Exemples
Endomorphismes de E
-
- L'ensemble des endomorphismes L(E) est une algèbre simple si E est un espace vectoriel de dimension finie.
Ce résultat est connu sous le nom de théorème de Burnside, il est démontré dans l'article Théorème d'Artin-Wedderburn.
Algèbre de groupe
Anneau Artinien
Propriétés héritées des modules
Article détaillé : Module semi-simple.Une algèbre semi-simple est aussi un module semi-simple. En conséquence, une telle structure hérite directement de propriétés:
Caractérisation d'une algèbre semi-simple
-
- Les trois propositions suivantes sont équivalentes :
- (i) L est une algèbre semi-simple.
- (ii) L est somme de sous-algèbres simples.
- (iii) Tout sous-algèbre est un facteur direct.
Les conséquences s'appliquent aussi aux algèbres :
-
- Supposons que L ne soit pas semi-simple, alors la somme de toutes les sous-algèbres simples de L est une sous-algèbre semi-simple, c'est la plus grande au sens de l'inclusion.
-
- Toute sous-algèbre d'une algèbre semi-simple est semi-simple.
Les démonstrations se trouvent dans l'article associés.
Lemme de Schur
Article détaillé : Lemme de Schur.Le lemme de Schur est un lemme technique explicitant la nature des morphismes entre une algèbre semi-simple et une algèbre simple. Il est à la fois simple à exprimer et à démontrer, cependant ses conséquences sont aussi nombreuses que profondes. Ici L désigne une algèbre semi-simple et S une algèbre simple sur A.
-
- Un morphisme de A dans L est soit nul soit injectif, un morphisme de L dans A est soit nul soit surjectif, si de plus L est simple alors un morphisme est soit nul soit bijectif. Si A est commutatif et si le polynôme minimal du morphisme est scindé, les seuls morphismes de S dans S sont les homothéties.
La structure d'un morphisme d'algèbres semi-simples est donc aisée à comprendre, elle correspond à une somme directe d'automorphismes de sous-algèbres simples et de morphisme nul.
Décomposition canonique
La décomposition d'une algèbre semi-simple en sous-algèbres simples n'est pas unique, pour obtenir une décomposition canonique, il est nécessaire de considérer la relation d'équivalence entre les sous-algèbres simples donnée par les isomorphismes. Deux algèbres simples sont en relation si et seulement s'il existe un isomorphisme de module entre elles. Soit Ni la somme des sous-algèbres d'une classe donnée. La décomposition suivante est canonique :
-
- Ni est la plus grande sous-algèbre ne contenant que des sous-algèbres simples isomorphes à Si et toutes ses sous-algèbres sont isomorphes à Si. L est somme directe des Ni.
-
- Avec les notations précédentes les sous-algèbres Ni sont appelées facteurs isotypiques de L.
Si une algèbre L ne contient que des sous-algèbre simples isomorphes deux à deux, alors l'algèbre L est qualifiée d'isotypique.
Le théorème d'Artin-Wedderburn énoncé ci-dessous, permet d'aller plus loin dans la compréhension de la structure.
Analyse des endomorphismes
Anneau simple
Déterminons l'ensemble des endomorphismes dans un cas simple, celui de l'anneau A considéré comme un module sur lui-même. Un tel module est noté ici AA. Une définition préalable est nécessaire :
-
- L'anneau opposé de A est l'anneau noté ici Aop muni de la multiplication définie par :
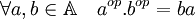
On dispose alors de la propriété suivante :
-
- L'ensemble des endomorphismes du module AA est isomorphe à AAop.
Ce qui revient à dire que les endomorphismes correspondent à l'anneau opposé de A.
En effet, si φ est un endomorphisme, il est entièrement déterminé par l'image de 1. En effet, si a est un élément de A, alors son image est égal à a. φ(1), l'égalité suivante permet de conclure :
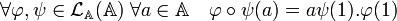
La structure d'anneau des endomorphisme est général aux algèbres, dans le cas d'une algèbre simple, le lemme de Schur indique que l'endomorphisme est soit nul, soit inversible ce qui démontre la propriété suivante :
-
- L'ensemble des endomorphismes d'une algèbre simple est un corps non nécessairement commutatif.
Dans le cas où l'algèbre simple est défini sur un corps commutatif algébriquement clos, les seuls automorphismes sont les homothéties.
-
- L'ensemble des endormorphismes d'une algèbre simple L sur un corps commutatif algébriquement clos K est isomorphe au centre de l'algèbre et à K.
Cette égalité s'écrit aussi : dim HomKL(L, L) = 1. Cette égalité signifie que l'algèbre sur le corps K des endomorphismes de L en tant qu'algèbre est de dimension 1.
Algèbre simple
Soit l un élément de L non nul, on utilise la définition et de la proposition suivante :
-
- L'ensemble des éléments a de A tel que a.l est égal zéro est un idéal bilataire maximal, on l'appelle idéal annulateur de A car cet idéal est indépendant de l'élément l non nul choisi.
Soit a un élément de l'idéal annulateur de l. L'homothétie de rapport a possède un noyau non nul, le lemme de Schur indique alors que cette homothétie est l'application nulle. L'élément a annule tout élément de L, les annulateurs des différents éléments non nuls de L sont donc tous égaux. Cette propriété montre aussi que l'ensemble des éléments annulant l est un idéal à droite. Si b est un élément de A, alors b.a.l = b.0 = 0, l'annulateur est donc aussi un idéal à gauche. Montrons enfin qu'il est maximal, pour cela il suffit de remarquer que tout élément hors de l'annulateur est inversible. C'est encore une conséquence directe du lemme de Schur. Il est donc inutile de considérer le cas d'une algèbre simple sur un anneau, il suffit d'étudier celui d'une algèbre simple sur un corps, en général gauche.
-
- Le quotient de A par l'idéal annulateur est un corps inclus dans celui du corps opposé des endomorphismes d'une algèbre simple.
Ce quotient est composée d'éléments qui s'identifient à des homothéties inversibles, ce sont donc bien des endomorphismes. Une algèbre simple sur un corps est la donnée d'un anneau L simple et d'un sous-corps du corps de l'opposé de l'algèbre des endomorphismes de L. Pour cette raison, seules les algèbres simples sur un corps sont étudiées.
Théorème d'Artin-Wedderburn
Article détaillé : Théorème d'Artin-Wedderburn.Énoncé du théorème
Le théorème d'Artin-Wedderburn est au cœur de la structure de l'algèbre, il exprime de la manière suivante :
-
- Un anneau semi-simple tel que tout idéal simple est de dimension finie sur son corps d'endomorphismes, est isomorphe à un produit d'algèbres d'endomorphismes de modules de dimension fini sur des corps à priori distincts et gauches.
L'analyse des endomorphismes d'une algèbre simple montre que le théorème se généralise immédiatement aux algèbres semi-simples. Ainsi un algèbre simple correspond à un anneau d'endomorphismes de module sur un corps gauche, et une algèbre correspond à la même structure adjointe d'un sous-corps du corps gauche.
Réciproquement une généralisation d'un théorème de Burnside (cf paragraphe Démonstration de Burnside de l'article Théorème d'Artin-Wedderburn) montre que l'algèbre des endomorphismes d'un module sur un corps gauche adjointe de la multiplication externe naturelle sur un sous-corps du corps définissant le module est une algèbre simple. De plus, un produit fini d'algèbres simples est une algèbre semi-simple. La réciproque du théorème d'Artin-Wedderburn est donc vérifiée.
L'unicité de la structure est assurée par l'unicité de la décomposition d'un module semi-simple en facteurs isotypiques.
Dans le cas où A est un corps commutatif algébriquement clos, alors l'analyse précédente montre que les corps des algèbres des endomorphismes sont tous égaux à A. On bénéficie alors de la proposition suivante :
-
- Si A est un corps commutatif algébriquement clos et L une algèbre semi-simple de dimension finie n, alors la dimension de chaque facteur isotypique est un carré parfait di2. De plus l'égalité suivante est vérifiée si h désigne le nombre de sous-algèbres simples incluses dans L :
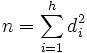
En effet, si di est la dimension d'un module simple Si de la i-ième composante isotypique de L, alors la i-ième algèbre est celle des endomorphisme de l'espace vectoriel sous-jacent de Si.
Centre de l'algèbre
Étudions le centre de l'algèbre dans le cas où l'algèbre est définie sur un corps commutatif algébriquement clos. Soient (Li) pour i variant de 1 à h la famille des sous-algèbres simples et c un élément du centre. Comme la famille des (Li) forme une somme directe égale à L, si l'on note pi le projecteur sur Li parallèlement à la somme directe des autres membres de la famille, on à l'égalité :
![c = \sum_{ij \in [1, h]} c_{ij} \quad avec \quad \forall i,j \in [1,h] \quad c_{ij}= p_j\circ c\circ p_i \;](/pictures/frwiki/99/cdedc5c68ffdded699da75343ab386a8.png)
Si i est différent de j, alors cij définit un morphisme de Li dans Lj. Le lemme de Schur indique qu'un tel morphisme est toujours nul. Si i est égal à j, alors cii correspond à un morphisme d'algèbre simple, c'est donc une homothétie d'un rapport à valeur dans K. En conclusion :
-
- Le centre de l'algèbre L est isomorphe à l'anneau somme directe d'autant de copies de K qu'il existe de sous-algèbres simples.
Cette égalité s'écrit maintenant si h désigne le nombre de sous-algèbres simples de l'algèbre L et C son centre.
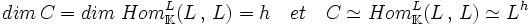
Notes et références
- ↑ Arthur Cayley Sur une nouvelle classe de théorèmes 1850
- ↑ Camille Jordan Commentaire sur Galois Math. Ann. 1869, réédition Œuvres Gauthier-Villars (Vol 1 page 211 à 230) 1961
- ↑ Marie Ennemond Camille Jordan Traité des substitutions et des équations algébriques 1870
- ↑ Marie Ennemond Camille Jordan Sur les équations de la Géométrie Comptes Rendus des Séances de l'Académie des Sciences. Paris. 1869
- ↑ Felix Klein Vergleichende Betrachtungen über neuere geometrische Forschungen A. Deichert 1872
- ↑ T. Y. Lam Representation of finite groups : A Hundred years, Part I Notice of the AMS Vol 45 p 365
- ↑ Ferdinand Georg Frobenius Uber die Darstellung der Endlichen Gruppen durch linear Substitutionen, Sitzungsber. Preuss Akad. Wiss Berlin 1897
- ↑ Heinrich Maschke Beweiss des Satzes, dass diejenigen endlichen linearen Substitutionesgruppen, in welchen einige durchgehends verschwindende Coefficienten auftenen intransitiv sind 1899
- ↑ William Burnside The Theory of Groups of Finite Order The University Press, Cambridge 1897
- ↑ Leonard Dickson Linear Groups- With an Exposition of the Galois Field Theory Courier Dover Publications 2003
- ↑ Elie Cartan Sur la structure des groupes de transformations finis et continus Paris, Librairie Vuibert, 1933
- ↑ Joseph Wedderburn On hypercomplex numbers London Mathematical Society 1907
- ↑ K H Parshall Joseph H M Wedderburn and the structure theory of algebras Arch. Hist. Exact Sci. (3-4) 32 pages 223 à 349 1985
- ↑ Paul Dubreil Emmy Noether Cahiers du séminaire d’histoire des mathématiques tome 7 pages 15 à 27 1986
- ↑ Emmy Noether Ideal Theorie in Ringbereichen Math. Annalen, t. 83 pages 24 à 66 1921
- ↑ Emil Artin Über einen Satz von J. H. Maclagan Wedderburn Abh. Math. Sem. Univ. Hamburg 5 pages 100 à 115 1927
- ↑ C. Hopkins Rings with minimal condition for left ideals Ann. of Math. II. Ser. 40 pages 712 à 730 1939
- ↑ N. Jacobson The radical and semisimplicity for arbitrary ring am. J. math. 67 pages 300 à 320 1945
Voir aussi
Liens externes
- (fr) Théorie des algèbres simples J.P. Serre Séminaire Henri Cartan
- (fr) Algèbre commutative A. Chambert-Loir
- (en) Finite group representation for the pure mathematician Peter Webb
- (fr) Théorie des algèbres semi-simples P. Cartier Séminaire Sophus Lie
Références
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
- N. Bourbaki, Algèbre commutative Chapitre VIII et IX Masson 1983
- Portail des mathématiques
Catégories : Algèbre commutative | Théorie des représentations | Structure externe -
Wikimedia Foundation. 2010.



