- Groupe De Lie
-
Groupe de Lie
En mathématiques, un groupe de Lie est un groupe qui est continu, c'est-à-dire que chaque élément du groupe peut être approché d'aussi près que l'on veut par une suite d'autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu'un groupe continu: il est en plus lisse, et on peut faire du calcul différentiel dessus. Ces groupes sont nommés ainsi en l'honneur du mathématicien norvégien Sophus Lie, qui les introduisit afin d'étudier certaines propriétés des équations différentielles.Sommaire
Histoire
Sophus Lie lui-même considérait que la théorie des groupes continus était née lors de l'hiver 1873-1874, mais le biographe Hawkins suggère que la théorie soit née des recherches effectuées par Lie durant les quatre années précédentes (de 1869 à 1873).
Une partie des idées initiales de Lie furent développées en collaboration avec Felix Klein, qu'il rencontrait quotidiennement durant les jours d'octobre des années 1869 à 1872, à Berlin d'abord, puis Paris, Gőttingen et Erlangen.
Les résultats de Lie furent publiés dans des journaux norvégiens lors de la décennie 1870, et son œuvre gagna rapidement le reste de l'Europe. En 1884, un jeune mathématicien allemand, Friedrich Engel travailla avec Lie à la création d'un exposé systématique de la théorie des groupes continus, lequel fut publié en trois volumes sous le titre Theorie der Transformationsgruppen, en 1888, 1890 et 1893.
Un développement important de la théorie fut ensuite réalisé par Wilhelm Killing. La généralisation par Elie Cartan, mena à la classification des algèbres de Lie semi-simples et aux travaux d'Hermann Weyl sur les représentations des groupes de Lie compacts.
La théorie des groupes de Lie fut exposée méthodiquement dans le langage mathématique moderne par Claude Chevalley.
Définitions
Une structure algébrique G est un groupe de Lie réel ou complexe lorsque :
- G est une variété différentiable réelle ou complexe ;
- G, munie de deux fonctions G×G
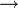 G (multiplication) et G
G (multiplication) et G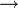 G (inversion), est un groupe ;
G (inversion), est un groupe ; - les applications de multiplication et d'inversion sont différentiables ou holomorphes.
Il est également possible de définir un groupe de Lie comme une variété différentielle munie d'opérations de groupe seulement continues. Cette définition est équivalente à la précédente et est une interprétation du 5e problème de Hilbert.
La dimension d'un groupe de Lie est définie comme sa dimension en tant que variété.
Il existe également une notion analogue de Groupe de Lie p-adique lorsque la variété différentielle sous-jacente est remplacée par un ensemble analytique p-adique. Ce sera le cas, par exemple, du groupe des points p-adiques d'un groupe algébrique.
Des premiers exemples simples
Un exemple simple est le groupe des matrices de rotation 2×2, noté SO(2,
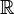 ) :
) : 
Il est paramétré par un seul angle λ : sa variété est donc unidimensionnelle (un cercle). C'est bien un groupe car l'inverse d'un élément de paramètre λ est donné par l'élément de paramètre −λ et le produit des éléments de paramètres λ et μ est donné par l'élément de paramètre λ+μ.
À l'inverse,
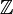 n'est pas un groupe continu, car il n'y a aucun élément entre 1 et 2.
n'est pas un groupe continu, car il n'y a aucun élément entre 1 et 2.Propriétés
Types de groupes de Lie
Les groupes de Lie sont classables selon leur propriétés algébriques (abélien, simple, semisimple, résoluble, nilpotent), ou bien topologiques (connexe, simplement connexe, compact).
Ils sont également usuellement classés en 4 groupes, représentés dans le tableau d'exemples plus bas :
- Groupes de Lie réels, basés sur le groupe
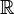 .
. - Groupes de Lie complexes, basés sur le groupe
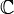 .
. - Groupes de Lie quaternioniques, basés sur le groupe des quaternions
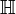 .
. - Groupes de Lie exceptionnels.
Homomorphismes et isomorphismes
Si G et H sont deux groupes de Lie (tous deux réels ou complexes), alors un homomorphisme de groupes de Lie f : G
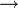 H est un homomorphisme de groupe qui est également une fonction différentiable ou holomorphe (il suffit en fait que f soit continue).
H est un homomorphisme de groupe qui est également une fonction différentiable ou holomorphe (il suffit en fait que f soit continue).La composition de deux homomorphismes de groupes de Lie est un homomorphisme de groupes de Lie et la classe de tous les groupes de Lie est une catégorie dont les flèches sont les homomorphismes de groupes de Lie. Deux groupes de Lie sont dit isomorphes s'il existe entre eux un homomorphisme bijectif dont la réciproque est également un homomorphisme.
La classe des groupes de Lie réels ou complexes de dimension n identifiés à isomorphisme près est un ensemble.
Algèbre de Lie associée à un groupe de Lie
Il est possible d'associer naturellement à tout groupe de Lie G une algèbre de Lie. Il existe deux manières équivalentes d'introduire cette algèbre de Lie. L'une consiste à introduire un espace de champs de vecteurs sur G, la seconde consiste à munir l'espace tangent en l'élément neutre d'un crochet de Lie, dérivant de l'expression locale de la loi interne de G.
Comme algèbre de champs de vecteurs
G désigne un groupe de Lie réel ou complexe de dimension n. Pour g un élément de G, l'application Lg : G
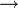 G définie par Lg(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dLg(Xh) = Xgh (où on note Xa la valeur du champ de vecteurs X au point a).
G définie par Lg(f) = gf est un difféomorphisme de la variété réelle ou complexe sous-jacente à G. Un champ de vecteurs X sur G est dit invariant à gauche lorsque pour tout couple d'élément g et h de G, on a : dLg(Xh) = Xgh (où on note Xa la valeur du champ de vecteurs X au point a).Pour toute variété différentielle réelle ou complexe M, l'espace vectoriel réel ou complexe des champs de vecteurs sur M, noté I(M), est muni d'une structure naturelle d'algèbre de Lie réelle ou complexe, dont le crochet est le crochet de champs de vecteurs. La naturalité signifie exactement que tout morphisme f:M
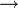 N entre variétés réelles ou complexes induit un morphisme d'algèbres de Lie f*I(M)
N entre variétés réelles ou complexes induit un morphisme d'algèbres de Lie f*I(M)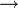 I(N). En particulier, pour M = N = G, on dispose d'automorphisme d'algèbres de Lie Lg *:I(G)
I(N). En particulier, pour M = N = G, on dispose d'automorphisme d'algèbres de Lie Lg *:I(G)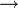 I(G). En particulier, l'ensemble des points fixes communs à tous les difféomorphismes Lg * est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont dits des champs de vecteurs invariants à gauche sur G.
I(G). En particulier, l'ensemble des points fixes communs à tous les difféomorphismes Lg * est une sous-algèbre de Lie de I(G), notée g. Ses éléments sont dits des champs de vecteurs invariants à gauche sur G.Comme espace tangent
Soit TeG l'espace tangent en e à G, e désignant l'élément neutre de G. L'application
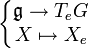 (où Xe est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel TeG
(où Xe est la valeur de X en l'élément neutre) est un isomorphisme linéaire. La structure d'algèbre de Lie de g se transporte donc, via cet isomorphisme, en une structure d'algèbre de Lie sur l'espace vectoriel TeGCette structure peut se définir directement. Supposons donnée f une carte locale de G en l'élément neutre e avec f(e)=0, alors, l'application produit lue dans la carte locale f est au second ordre près :
f(f-1(a).f-1(b))=a+b+B(a,b)+...
où B est une forme bilinéaire antisymétrique. La structure d'algèbre de Lie sur TeG est donnée par :
- [X,Y] = B(X,Y).
Application exponentielle
Dans la première présentation, tout vecteur X de g est par définition un vecteur invariant à gauche sur G. L'invariance à gauche implique que son flot est globalement défini. L'exponentielle de X est définie comme l'image au temps 1 de l'élément neutre. Plus précisément, il existe une unique fonction c :
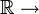 G dont la dérivée est donnée par :
G dont la dérivée est donnée par :- c'(t) = X[c(t)] [eq.1].
et c(0) = 1
Elle possède la propriété remarquable suivante :
- c(s + t) = c(s).c(t) [eq.2]
pour tous s et t.
On peut écrire : ev = c(1)
Une reparamétrisation incluant la variable t montre
- c(t) = etv [eq.3]
On peut vérifier : c(0) = 1; d(c(t)) / dt = vetv ; d(c(0)) / dt = X[c(0)] = v .
Cette fonction est également appelée fonction exponentielle et relie l'algèbre de Lie g au groupe de Lie G. Elle définit un difféomorphisme entre un voisinage de 0 dans g et un voisinage de e dans G. Toutefois, en général, l'application exponentielle n'est pas surjective.
Un sous-groupe à un paramètre de G est une application différentiable c
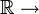 G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément X de g vérifiant : c(t) = etv.
G vérifiant l'identité eq.2 ci-dessus. À tout sous-groupe à un paramètre c est associé un unique élément X de g vérifiant : c(t) = etv.Classification algébrique des groupes de Lie
Plusieurs groupes de Lie peuvent partager la même algèbre de Lie associée. Cependant, à toute algèbre de Lie g correspond un groupe de Lie simplement connexe G, unique à isomorphisme près. De plus cet isomorphisme est uniquement déterminé par l'isomorphisme d'algèbre de Lie associé. Tout groupe de Lie connexe dont l'algèbre de Lie est isomorphe à g se réalise comme quotient de G par un sous-groupe normal discret.
Un groupe de Lie connexe est simple, semisimple, résoluble, nilpotent ou abélien si et seulement si son algèbre de Lie associée possède la propriété de même nom. En particulier, la classification des algèbres de Lie semi-simples donne une classification des groupes de Lie simplement connexes et semi-simples.
Exemples
Groupes de Lie réels
Groupe de Lie Description Propriétés Algèbre de Lie Description Dimension 
Espace euclidien muni de l'addition Abélien; Simplement connexe, non compact 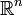
Le crochet de Lie est nul n 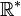
Nombres réels non nuls munis de la multiplication Abélien; Non connexe, non compact 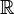
Le crochet de Lie est nul 1 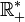
Nombres réels strictement positifs munis de la multiplication Abélien; Simplement connexe, non compact 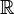
Le crochet de Lie est nul 1 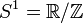
Nombres complexes de module 1 munis de la multiplication Abélien; Connexe, non simplement connexe, compact 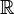
Le crochet de Lie est nul 1 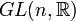
Groupe général linéaire : matrices réelles n×n inversibles Non connexe, non compact 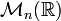
Matrices n×n, le crochet de Lie étant le commutateur n² 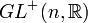
matrices réelles n×n à déterminant positif Simplement connexe, non compact 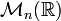
Matrices n×n, le crochet de Lie étant le commutateur n² 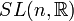
Groupe spécial linéaire : matrices réelles de déterminant 1 Simplement connexe, non compact si n > 1 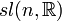
Matrices carrées de trace nulle, le crochet de Lie étant le commutateur n²-1 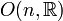
Groupe orthogonal : matrices orthogonales réelles Non connexe, compact 
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur; 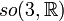 est isomorphe à
est isomorphe à 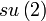 et
et 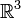 muni du produit vectoriel
muni du produit vectorieln(n - 1)/2 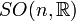
Groupe spécial orthogonal : matrices orthogonales réelles de déterminant 1 Simple et semisimple pour n=3 et n≥5; Connexe, compact, non simplement connexe pour n≥2 
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur n(n - 1)/2 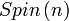
Groupe Spin Simple et semisimple pour n=3 et n≥5; Simplement connexe, compact 
Matrices antisymétriques carrées réelles, le crochet de Lie étant le commutateur n(n - 1)/2 
Groupe symplectique : matrices symplectiques réelles Simple, semisimple; Non compact 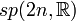
Matrices réelles satisfaisant JA + ATJ = 0 où J est la matrice antisymétrique standard n(2n + 1) Groupes de Lie complexes
Les dimensions sont données sur
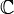 (sauf pour les groupes unitaires où elles sont données sur
(sauf pour les groupes unitaires où elles sont données sur 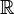 ). Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.
). Tout groupe ou algèbre de Lie complexe peut être vu comme un groupe ou une algèbre de Lie réel de dimension double.Groupe de Lie Description Propriétés Algèbre de Lie Description Dimension 
Espace euclidien muni de l'addition Abélien; Simplement connexe, non compact 
Le crochet de Lie est nul n 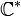
Nombres complexes non nuls munis de la multiplication Abélien; Non simplement connexe, non compact 
Le crochet de Lie est nul 1 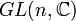
Groupe général linéaire : matrices complexes n×n inversibles Simplement connexe, non compact; Isomorphe à 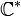 pour n=1
pour n=1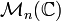
Matrices n×n, le crochet de Lie étant le commutateur n² 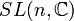
Groupe spécial linéaire : matrices complexes de déterminant 1 Simple, semisimple; Simplement connexe, non compact pour n≥2 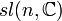
Matrices carrées de trace nulle, le crochet de Lie étant le commutateur (n²-1) 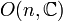
Groupe orthogonal : Matrices orthogonales complexes Non connexe, non compact pour n≥2 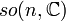
matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur n(n-1) 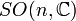
Groupe spécial orthogonal : matrices orthogonales complexes de déterminant 1 Simple et semisimple pour n=3 et n≥5; Non simplement connexe, non compact pour n≥2 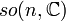
Matrices antisymétriques carrées complexes, le crochet de Lie étant le commutateur n(n-1) 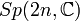
Groupe symplectique : matrices symplectiques complexes Simple et semisimple; Non compact 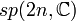
Matrices complexes satisfaisant JA+ATJ=0 où J est la matrice antisymétrique standard 2n(2n+1) 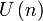
Groupe unitaire : matrices unitaires n×n complexes Non simplement connexe, compact; Isomorphe à S1 pour n=1 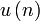
Matrices carrées complexes A vérifiant A=-A*, le crochet de Lie étant le commutateur n² 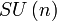
Groupe spécial unitaire : matrices unitaires complexes n×n de déterminant 1 Simple et semisimple pour n≥2; Simplement connexe, compact 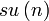
Matrices carrées complexes de traces nulles A vérifiant A=-A*, le crochet de Lie étant le commutateur n²-1 Groupes de Lie quaternioniques
Les dimensions sont données sur
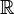 .
.Groupe de Lie Description Propriétés Algèbre de Lie Description Dimension 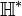
Quaternions non nuls munis de la multiplication Simplement connexe, non compact 
Quaternions, le crochet de Lie étant le commutateur 4 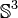
Quaternions de module 1 munis de la multiplication, également noté 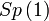
Simple, semisimple; Simplement connexe, compact; Topologiquement une sphère, isomorphe à 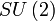 et
et 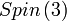
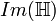
Quaternions de partie réelle nulle, le crochet de Lie étant le produit vectoriel; Isomorphe aux vecteurs réels de dimension 3, également isomorphe à 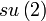 et
et 
3 
Groupe compact symplectique : matrices unitaires n×n quaternioniques Simple, semisimple; Compact, simplement connexe 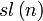
Matrices quaternioniques carrées A vérifiant A=-A*, le crochet de Lie étant le commutateur n(2n + 1) Groupes de Lie exceptionnels
On répertorie 5 Groupes de Lie dits exceptionnels, notés respectivement E6, E7, E8, F4 & G2
Voir aussi
Articles connexes
- Espace homogène
- Action de groupe de Lie
- Action hamiltonienne
- Représentation
- Représentation coadjointe
- Application moment
- E8 (mathématiques)
- Groupe algébrique (l'analogue algébrique des groupes de Lie, ce sont des variétés algébriques munies d'une structure de groupe).
- Groupe classique
Sites externes
- Site du Projet Atlas de résolution des représentations des groupes de Lie (National Science Foundation, American Institute of Mathematics)
Bibliographie
- Rached Mneimné et Frédéric Testard, Introduction à la théorie des groupes de Lie classiques, Hermann, 2005.
- Roger Godement, Introduction à la théorie des groupes de Lie, Springer, 2004.
- Portail des mathématiques
Catégories : Article à désacadémiser | Groupe de Lie | Physique quantique | Structure algébrique topologique
Wikimedia Foundation. 2010.
