- Suite de Fibonacci
-
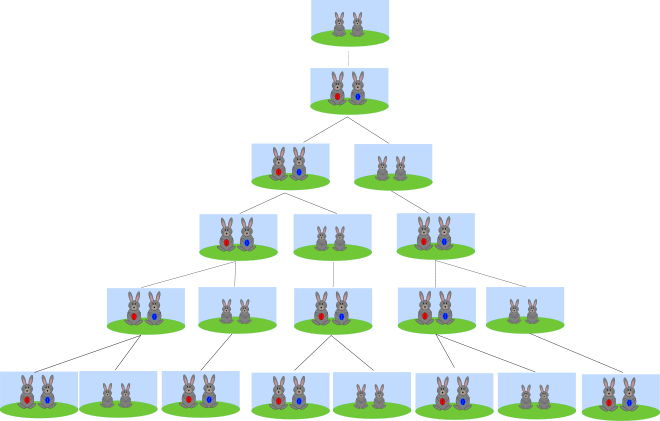
La suite de Fibonacci est une suite d'entiers très connue. Elle doit son nom à Leonardo Fibonacci, dit Leonardo Pisano, un mathématicien italien du XIIIe siècle qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, décrit la croissance d'une population de lapins :
- « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? »
Ce problème est à l'origine de la suite dont le n-ième terme correspond au nombre de paires de lapins au n-ème mois. Dans cette population (idéale), on suppose que :
- au (début du) premier mois, il y a juste une paire de lapereaux ;
- les lapereaux ne procréent qu'à partir du (début du) troisième mois ;
- chaque (début de) mois, toute paire susceptible de procréer engendre effectivement une nouvelle paire de lapereaux ;
- les lapins ne meurent jamais (donc la suite de Fibonacci est strictement croissante).
Présentation mathématique
Formule de récurrence
Notons
 le nombre de couples de lapins au début du mois n. Jusqu’à la fin du deuxième mois, la population se limite à un couple (ce qu'on note :
le nombre de couples de lapins au début du mois n. Jusqu’à la fin du deuxième mois, la population se limite à un couple (ce qu'on note :  ). Dès le début du troisième mois, le couple de lapins a deux mois et il engendre un autre couple de lapins. On note alors
). Dès le début du troisième mois, le couple de lapins a deux mois et il engendre un autre couple de lapins. On note alors  . Plaçons-nous maintenant au mois
. Plaçons-nous maintenant au mois  et cherchons à exprimer ce qu'il en sera deux mois plus tard (n + 2) :
et cherchons à exprimer ce qu'il en sera deux mois plus tard (n + 2) :  désigne la somme des couples de lapins au mois n + 1 et des couples nouvellement engendrés. Or, n'engendrent au mois (n + 2) que les couples pubères, c'est-à-dire ceux qui existent deux mois auparavant. On a donc :
désigne la somme des couples de lapins au mois n + 1 et des couples nouvellement engendrés. Or, n'engendrent au mois (n + 2) que les couples pubères, c'est-à-dire ceux qui existent deux mois auparavant. On a donc :pour tout entier n strictement positif. On choisit alors de poser
 , de manière que cette équation soit encore vérifiée pour n = 0.
, de manière que cette équation soit encore vérifiée pour n = 0.On obtient ainsi la forme récurrente de la suite de Fibonacci : chaque terme de cette suite est la somme des deux termes précédents ; pour obtenir chacun de ces deux termes, il faut faire la somme de leurs termes précédents… et ainsi de suite, jusqu'à ce que ces deux termes soient les deux termes initiaux,
 et
et  , qui sont connus.
, qui sont connus.Nombres de Fibonacci
Les termes de cette suite sont appelés nombres de Fibonacci (suite A000045 de l’OEIS) :


























… 
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 ... 
Expression fonctionnelle
On souhaite établir une expression fonctionnelle de la suite de Fibonacci, c'est-à-dire une expression telle que le calcul du nombre de couples pour une valeur de
 donnée ne présuppose la connaissance d’aucun nombre de couples pour une quelconque autre valeur de
donnée ne présuppose la connaissance d’aucun nombre de couples pour une quelconque autre valeur de  , ce que ne permet pas la formule de récurrence. Comme la suite de Fibonacci est linéairement récurrente d’ordre deux, on peut écrire son équation caractéristique. On obtient une équation du second degré :
, ce que ne permet pas la formule de récurrence. Comme la suite de Fibonacci est linéairement récurrente d’ordre deux, on peut écrire son équation caractéristique. On obtient une équation du second degré :Le calcul du discriminant de cette équation donne les deux solutions du polynôme :
où φ est le nombre d'or.
Les suites (φn) et (φ'n) engendrent alors l'espace vectoriel des suites vérifiant un + 2 = un + 1 + un. Il en résulte que :
 (α et β sont des constantes à déterminer à partir de
(α et β sont des constantes à déterminer à partir de  et
et  .)
.)
Les conditions initiales
 et
et  conduisent au système suivant :
conduisent au système suivant :ce qui donne :
Nous obtenons finalement l'expression fonctionnelle recherchée, qui porte le nom de formule de Binet :

Quand n tend vers l'infini,
 est équivalent à
est équivalent à  . Plus précisément, φn tend vers l'infini et φ'n tend vers zéro car | φ' | < 1 < φ.
. Plus précisément, φn tend vers l'infini et φ'n tend vers zéro car | φ' | < 1 < φ.En fait, dès le rang n = 1, le deuxième terme
 est assez petit pour que les nombres de Fibonacci puissent être obtenus uniquement à partir du premier terme :
est assez petit pour que les nombres de Fibonacci puissent être obtenus uniquement à partir du premier terme : est l'entier le plus proche de
est l'entier le plus proche de  (et il lui est supérieur ou inférieur, selon la parité de n).
(et il lui est supérieur ou inférieur, selon la parité de n).
Il existe d'autres démonstrations de la formule de Binet, telles que la transformation en Z et la technique des fonctions génératrices.
Remarquons qu'une fois découverte, cette formule se démontre aussi par récurrence, y compris pour n entier négatif quand la suite est prolongée comme ci-dessous.
La suite pour les nombres négatifs
En général, on n'étudie pas les nombres de Fibonacci pour des valeurs négatives de n, bien qu'ils existent et soient facilement déterminables avec la formule récurrente. Il existe ainsi une règle très simple pour calculer ces nombres quand n < 0 :
- si n est pair alors

- si n est impair alors

ou plus généralement :

Ainsi, autour de 0, la séquence est :
Limite des quotients
Comme l'avait déjà remarqué Johannes Kepler[1], le taux de croissance des nombres de Fibonacci, c'est-à-dire
 , converge vers le nombre d'or, noté φ.
, converge vers le nombre d'or, noté φ.En effet, puisque la suite
 est équivalente à
est équivalente à  (cf supra, section Expression fonctionnelle), la suite
(cf supra, section Expression fonctionnelle), la suite  est équivalente à
est équivalente à  qui est donc sa limite.
qui est donc sa limite.En fait plus généralement, toutes les suites vérifiant la même relation de récurrence que la suite de Fibonacci (cf infra, section Suites de Fibonacci généralisées) satisfont cette propriété.
Bases et espaces vectoriels
- La dénomination de « suite de Fibonacci généralisée » est attribuée plus généralement à toute fonction
 définie sur
définie sur  vérifiant pour tout entier naturel n,
vérifiant pour tout entier naturel n,  . Ces fonctions sont précisément celles pour lesquelles il existe des nombres a et b, tels que pour tout entier naturel n,
. Ces fonctions sont précisément celles pour lesquelles il existe des nombres a et b, tels que pour tout entier naturel n,  . Ainsi, l'ensemble des suites de Fibonacci est un espace vectoriel, et les suites
. Ainsi, l'ensemble des suites de Fibonacci est un espace vectoriel, et les suites  et
et  en forment une base.
en forment une base.
- Le nombre d'or est la racine positive de l'équation du second degré
 , ainsi
, ainsi  . Si on multiplie les deux côtés par
. Si on multiplie les deux côtés par  , on obtient
, on obtient  , donc la fonction
, donc la fonction  est une suite de Fibonacci. La racine négative de l'équation du second degré,
est une suite de Fibonacci. La racine négative de l'équation du second degré,  , possède les mêmes propriétés, et les deux fonctions linéairement indépendantes
, possède les mêmes propriétés, et les deux fonctions linéairement indépendantes  et
et  , forment une autre base de l'espace vectoriel.
, forment une autre base de l'espace vectoriel.
Algorithmes de calcul des nombres de Fibonacci
Avec la formule de Binet
Calculer les nombres de Fibonacci à partir du nombre d'or est une possibilité très pratique. Néanmoins, la précision de calcul de la racine carrée génère des erreurs d'arrondis pour des valeurs assez grandes dépendant du système utilisé. En général, on obtient les bonnes valeurs jusqu’à
 = 308 061 521 170 130, sur ordinateur ou sur calculatrice.
= 308 061 521 170 130, sur ordinateur ou sur calculatrice.Notons qu’au-delà de
 , les calculs dépassent les possibilités de calcul en notation entière, et sont alors représentés en notation scientifique. Les premiers chiffres significatifs sont alors de nouveau bien représentés par cette formule.
, les calculs dépassent les possibilités de calcul en notation entière, et sont alors représentés en notation scientifique. Les premiers chiffres significatifs sont alors de nouveau bien représentés par cette formule.Détail d’un exemple d'application faisable à partir d'une calculatrice : calcul de
 .
.Le nombre d’or vaut
 1,618 033 988 749 89…, et d'après la formule de Binet,
1,618 033 988 749 89…, et d'après la formule de Binet,  est l'entier le plus proche du réel
est l'entier le plus proche du réel  , qui le dépasse à peine. Compte tenu de l'ordre de grandeur de ce réel, le théorème des accroissements finis permet de s'assurer que pour le calculer à 0,5 près par défaut, 1,618 033 988 749 89 est une approximation suffisante de φ.
, qui le dépasse à peine. Compte tenu de l'ordre de grandeur de ce réel, le théorème des accroissements finis permet de s'assurer que pour le calculer à 0,5 près par défaut, 1,618 033 988 749 89 est une approximation suffisante de φ.On trouve que le réel (1,618 033 988 749 89)50/√5 est à peine inférieur à l'entier 12 586 269 025, d'où

si bien que

Algorithme récursif naïf
La mise en œuvre récursive naïve qui suit la définition de la suite de Fibonacci est immédiate en appliquant la fonction donnée par l'algorithme suivant :
fonction fibo(n): // entrée : un nombre entier n // sortie : le terme de rang n de la suite de Fibonacci // // deux premiers cas : fibo(0) est égal à 0 et fibo(1) est égal à 1 si (n <= 1) retourner n // récurrence à partir du terme de rang 2 sinon retourner fibo(n - 1) + fibo(n - 2) fin de la fonction
Ce n'est cependant pas une façon judicieuse de calculer la suite de Fibonacci, car on calcule de nombreuses fois les mêmes valeurs (à moins d'employer une technique de mémoization). Le temps de calcul s'avère exponentiel.
Algorithme linéaire
Un moyen bien plus efficace de calculer la suite de Fibonacci consiste à calculer simultanément deux valeurs consécutives de la suite, c'est-à-dire en commençant avec les deux premières valeurs 0 et 1, et en remplaçant répétitivement le premier nombre par le second, et le second nombre par la somme des deux.
En Python, un tel algorithme itératif donne :
def fibo(n): f_n_1 = 1 # F_{-1} = 1 f_n = 0 # F_0 = 0 for i in range(n): # n fois (f_n_1, f_n) = (f_n, f_n + f_n_1) return f_n
De manière équivalente, on peut écrire une fonction récursive terminale :
def fibo(n, f_n_1 = 1, f_n = 0): # (n, F_{n-1}, F_n) if (n == 0): # cas de base return f_n else: # récurrence return fibo(n - 1, f_n, f_n + f_n_1)
Le temps de calcul est à chaque fois proportionnel à n et l'espace mémoire occupé constant.
Algorithme logarithmique
En utilisant la relation matricielle suivante, que l'on montre par récurrence :
ou avec les propriétés de la suite de Fibonacci, on obtient :
En prenant bien soin de ne pas calculer deux fois les mêmes éléments, on obtient alors un algorithme dont le temps de calcul est proportionnel au logarithme de n. Voici un exemple de programme en Python :
def fibo2(n): """Renvoie F_{n-1}, F_n""" if (n == 0): # cas de base return 1, 0 # F_{-1}, F_0 else: # récurrence f_k_1, f_k = fibo2(n//2) # F_{k-1}, F_k avec k = n/2 f2_k = f_k**2 # F_k^2 if n%2 == 0: # n pair return f2_k + f_k_1**2, f_k*f_k_1*2 + f2_k # F_{2k-1}, F_{2k} else: # n impair return f_k*f_k_1*2 + f2_k, (f_k + f_k_1)**2 + f2_k # F_{2k}, F_{2k+1} def fibo(n): """Renvoie F_n""" return fibo2(n)[1]
En retravaillant les relations de récurrence pour le cas pair on obtient :
Et donc :
Curiosité algorithmique
Le programme FRACTRAN défini par la liste de fractions [23/95, 57/23, 17/39, 130/17, 11/14, 35/11, 19/13, 1/19, 35/2, 13/7, 7] et appliqué à l'entier 3 génère une suite qui contient tous les termes de la forme 2a3b, où a et b sont deux termes consécutifs de la suite de Fibonacci.
Propriétés de la suite de Fibonacci
La suite de Fibonacci présente de remarquables propriétés. En voici quelques-unes, démontrées à partir de la formule de Binet ou par récurrence (pour certaines, on peut aussi utiliser le calcul matriciel et les identités données au paragraphe précédent). Nous donnons également quelques propriétés liant la suite de Fibonacci et la suite des nombres de Lucas
 définie par la même relation de récurrence mais avec pour initialisation
définie par la même relation de récurrence mais avec pour initialisation  et
et  , et pour laquelle l'analogue de la formule de Binet est :
, et pour laquelle l'analogue de la formule de Binet est :  .
.Propriété 1 :
 ou encore :
ou encore :  Démonstration
DémonstrationPropriété 2 :

- C'est le cas r = 1 de la propriété 1.
Propriété 3 :

- C'est le cas q = p − 1 de la propriété 2.
Propriété 4 :

- C'est le cas q = 1 de la propriété 1.
Propriété 5 :
 (identité de Catalan) et
(identité de Catalan) et  (identité de Cassini).
(identité de Cassini).- L'identité de Catalan est le cas r = p − q de la propriété 1. L'identité de Cassini est le cas q = 1 de celle de Catalan (c'est donc aussi le cas r = p − 1 de la propriété 4).
- Corollaire 1 :

DémonstrationPour prouver la première propriété, il suffit de considérer l'identité de Cassini
 et de résoudre l'équation du second degré obtenue d'inconnue
et de résoudre l'équation du second degré obtenue d'inconnue  , à savoir
, à savoir 
La suite de Fibonnacci apparaît également comme une suite récurrente du premier ordre, mais non linéaire.
Pour en déduire la fin du corollaire, on fait un petit décalage d'indice dans la formule précédente, en remarquant que les termes de la suite de Fibonacci sont entiers.
- Corollaire 2 :

Démonstration
Propriété 6 :
 en particulier
en particulier  Démonstration
DémonstrationLe cas nk = 0 est immédiat et le cas k < 0 se déduit du cas k > 0. On peut donc supposer k > 0 et
 .
.En particulier,
Propriété 7 : Pour tout entier naturel n différent de 4, si
 est premier, alors n est premier.
est premier, alors n est premier.- Ou par contraposée : si n est composé alors
 aussi. En effet, supposons n = mk avec m et k entiers strictement supérieurs à 1. Comme n est supposé différent de 4, l'un au moins des deux facteurs est strictement supérieur à 2 : par exemple m > 2. D'après la propriété 6,
aussi. En effet, supposons n = mk avec m et k entiers strictement supérieurs à 1. Comme n est supposé différent de 4, l'un au moins des deux facteurs est strictement supérieur à 2 : par exemple m > 2. D'après la propriété 6,  est alors un diviseur propre de
est alors un diviseur propre de  , qui n'est donc pas premier.
, qui n'est donc pas premier. - La réciproque est fausse, car 2 est premier alors que
 ne l'est pas ; de façon moins triviale,
ne l'est pas ; de façon moins triviale,  .
.
Propriété 8 :
 où
où  désigne le PGCD de nombres entiers.Démonstration
désigne le PGCD de nombres entiers.DémonstrationSoient
 et
et  (qui sont tous deux positifs ou nuls).
(qui sont tous deux positifs ou nuls).- D'après la propriété 6,
 et
et  et donc
et donc  .
. - D'après le théorème de Bézout, il existe deux entiers x et y tels que d = ax + by. Posons alors p = ax et q = by. Comme
 divise
divise  et
et  , il divise aussi
, il divise aussi  et
et  d'après la propriété 6, donc également
d'après la propriété 6, donc également  d'après la propriété 2, autrement dit
d'après la propriété 2, autrement dit  .
. - Ainsi,
 est égal ou opposé à D. Comme il est positif ou nul (car d l'est), nous en concluons que
est égal ou opposé à D. Comme il est positif ou nul (car d l'est), nous en concluons que  .
.
- En particulier,
 c.-à-d. que
c.-à-d. que  et
et  sont premiers entre eux.
sont premiers entre eux.
Propriété 9 :
 En particulier :Démonstration
En particulier :DémonstrationPropriété 10 :
 Démonstration
DémonstrationPar somme et différence, il revient au même de démontrer que
La seconde égalité est immédiate et la première résulte de la propriété 9 :
Propriété 11 :
 Démonstration
DémonstrationLes deux premières égalités s'obtiennent par somme télescopique :
La troisième s'en déduit en les additionnant, de façon différente suivant la parité de n :
Propriété 12 :
 où les
où les  sont des coefficients binomiaux.Démonstration
sont des coefficients binomiaux.DémonstrationEn réalité, la somme n'est pas infinie car tous les
 sont nuls pour k > n - k mais on sommera sur
sont nuls pour k > n - k mais on sommera sur  pour faciliter les démonstrations.
pour faciliter les démonstrations.Par récurrence d'ordre 2 sur n.
- Initialisation
- (n = 0) :
 et
et 
- (n = 1) :
 et
et 
- Hypothèses de récurrence :
- au rang n,

- au rang n + 1,

- Hérédité (rang n + 2) :

-
- (Formule du triangle de Pascal)
-

-
- Car
 )
)
- Car
-

-
- (Hypothèse de récurrence, changement de variable
 )
)
- (Hypothèse de récurrence, changement de variable
-
 (Hypothèse de récurrence)
(Hypothèse de récurrence) (Définition de la suite de Fibonacci)
(Définition de la suite de Fibonacci)
- Cela signifie que, dans un triangle de Pascal, les nombres de Fibonacci s'obtiennent en sommant les termes situés sur une diagonale (du bas vers la droite).
Bestiaire de formules
Divisibilité des nombres de Fibonacci
Une première approche de la question de la divisibilité de
 par un entier a consiste à étudier la suite des restes de
par un entier a consiste à étudier la suite des restes de  modulo a : cette suite (rn) vérifie (dans Z/aZ) la même récurrence (rn + 2 = rn + 1 + rn) et est donc périodique de période au plus a2 (les longueurs des périodes en fonction de n forment la suite des périodes de Pisano (en) suite A001175 de l’OEIS) ; on en déduit que pour tout a, il existe n inférieur ou égal à a2 tel que
modulo a : cette suite (rn) vérifie (dans Z/aZ) la même récurrence (rn + 2 = rn + 1 + rn) et est donc périodique de période au plus a2 (les longueurs des périodes en fonction de n forment la suite des périodes de Pisano (en) suite A001175 de l’OEIS) ; on en déduit que pour tout a, il existe n inférieur ou égal à a2 tel que  (et donc
(et donc  ) soit divisible par a. Plus précisément, l'étude de cette récurrence dans le corps Z/pZ (où p est un nombre premier) amène à des formules analogues à la formule de Binet, d'où l'on déduit finalement (selon que 5 est ou n'est pas un carré modulo p ; voir la loi de réciprocité quadratique) que
) soit divisible par a. Plus précisément, l'étude de cette récurrence dans le corps Z/pZ (où p est un nombre premier) amène à des formules analogues à la formule de Binet, d'où l'on déduit finalement (selon que 5 est ou n'est pas un carré modulo p ; voir la loi de réciprocité quadratique) que  est divisible par 5, et que si p est premier autre que 5,
est divisible par 5, et que si p est premier autre que 5,  est divisible par p si p est de la forme 5m+1 ou 5m+4, et
est divisible par p si p est de la forme 5m+1 ou 5m+4, et  est divisible par p sinon (des résultats un peu plus précis peuvent être obtenus ; ainsi, dans le premier cas,
est divisible par p sinon (des résultats un peu plus précis peuvent être obtenus ; ainsi, dans le premier cas,  est divisible par p si (p-1)/2 est pair). Enfin, si p>2 est premier et divise
est divisible par p si (p-1)/2 est pair). Enfin, si p>2 est premier et divise  , pk divise
, pk divise  , et 2k+1 divise
, et 2k+1 divise  ; ces derniers résultats sont des conséquences du lemme de Hensel[2],[3].
; ces derniers résultats sont des conséquences du lemme de Hensel[2],[3].Primalité des nombres de Fibonacci
On ignore s'il existe une infinité de nombres de Fibonacci premiers. On sait que
 divise
divise  (voir Propriétés, Propriété 6), et donc que, pour tout
(voir Propriétés, Propriété 6), et donc que, pour tout  , si
, si  est premier, alors
est premier, alors  est premier, mais la réciproque est fausse (
est premier, mais la réciproque est fausse ( est le premier contre-exemple non trivial). À ce jour (août 2011), le plus grand nombre premier de Fibonacci connu est
est le premier contre-exemple non trivial). À ce jour (août 2011), le plus grand nombre premier de Fibonacci connu est  [4] et le plus grand nombre de Fibonacci probablement premier connu est
[4] et le plus grand nombre de Fibonacci probablement premier connu est  [5], qui possède 341 905 chiffres.
[5], qui possède 341 905 chiffres.Depuis 1964, on connait des suites
 vérifiant en même temps les trois conditions suivantes :
vérifiant en même temps les trois conditions suivantes :Par exemple:
- suite A082411 de l’OEIS (John Nicol, 1999) déterminée par :
- suite A083216 de l’OEIS (Herbert Wilf (en), 1990) déterminée par :
- et suite A083103 de l’OEIS (Robert Graham, 1964 ; non vérifiée, selon l'OEIS) déterminée par:
Applications
- En poésie, un fib est un petit poème, sorte de haïku, dont le nombre de pieds des premiers vers correspond aux premiers nombres de la suite (1, 1, 2, 3, 5, 8).
- La suite de Fibonacci apparaît dans de nombreux problèmes de dénombrement. Par exemple, le terme d'indice n (pour n supérieur ou égal à 2) de la suite de Fibonacci permet de dénombrer le nombre de façons de parcourir un chemin de longueur n-1 en faisant des pas de 1 ou 2. Ce problème apparaît d'aillleurs très tôt en Inde, sous le nom maatraameru (montagne de cadence), dans le travail du grammairien de sanskrit Pingala, le Chhandah-shastra, (l'art de la Prosodie), 450 ou 200 av. J.-C.). Le mathématicien indien Virahanka (en) en a donné des règles explicites au VIIIe siècle. Le philosophe indien Acharya Hemachandra (en) (c. 1150) (et aussi Gopala, c. 1135) ont revisité le problème de manière assez détaillée. En sanskrit en effet, les voyelles peuvent être longues (L) ou courtes (C), et Hemachandra a souhaité calculer combien on peut former de cadences différentes d'une longueur donnée, chaque cadence étant définie par les longueurs des voyelles qui la constituent. Si la voyelle longue est deux fois plus longue que la courte, les solutions sont, en fonction de la longueur totale de la cadence :
-
- 1 C → 1
- 2 CC,L → 2
- 3 CCC, CL, LC → 3
- 4 CCCC, CCL, CLC, ,LCC, LL → 5
- 5 CCCCC, CCCL, CCLC, CLCC, LCCC, CLL, LCL, LLC → 8
- Le nombre de cadences fait apparaître les termes de la suite de Fibonacci. En effet, une cadence de longueur n peut être constituée en ajoutant C à une cadence de longueur n-1, ou L à une cadence de longueur n-2. Ainsi le nombre de cadences de longueur n est la somme des deux nombres précédents de la série. Ce problème est également équivalent au dénombrement des emballages de longueur n donnée, constitué d'articles de longueur 1 ou 2, tel qu'on le trouve par exemple dans The Art of Computer Programming de Donald Knuth.
- Les nombres de Fibonacci interviennent dans l'étude de l'exécution de l'algorithme d'Euclide qui détermine le plus grand commun diviseur de deux entiers.
- Matiyasevich a montré que les nombres de Fibonacci pouvaient être définis par une équation diophantienne, ce qui a conduit à la résolution du dixième problème d'Hilbert. En 1975, Jones en a déduit que, pour des valeurs de x et y entières positives ou nulles, les valeurs positives du polynôme 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y étaient exactement les nombres de Fibonacci. Ces valeurs positives s'obtiennent d'ailleurs en attribuant pour valeurs à x et y deux nombres de Fibonacci successifs.
- Les nombres de Fibonacci apparaissent dans la formule des diagonales du triangle de Pascal (voir Propriétés, Propriété 12).
- Une bonne approximation d'un rectangle d'or peut être construite à l'aide de carrés dont les côtés sont égaux aux nombres de Fibonacci.
- Une spirale logarithmique peut être approchée de la manière suivante : on commence à l'origine d'un repère cartésien, on se déplace de
 unités vers la droite, puis de
unités vers la droite, puis de  unités vers le haut, on se déplace de
unités vers le haut, on se déplace de  unités vers la gauche, ensuite de
unités vers la gauche, ensuite de  unités vers le bas, puis de
unités vers le bas, puis de  unités vers la droite, etc. Cela ressemble à la construction mentionnée dans l'article sur le nombre d'or. Les nombres de Fibonacci apparaissent souvent dans la nature lorsque des spirales logarithmiques sont construites à partir d'une unité discrète, telles que dans les tournesols ou dans les pommes de pin. Depuis l'antiquité grecque, la suite est également utilisée par les architectes afin de définir l'agencement et les proportions des différentes pièces d'un logement.
unités vers la droite, etc. Cela ressemble à la construction mentionnée dans l'article sur le nombre d'or. Les nombres de Fibonacci apparaissent souvent dans la nature lorsque des spirales logarithmiques sont construites à partir d'une unité discrète, telles que dans les tournesols ou dans les pommes de pin. Depuis l'antiquité grecque, la suite est également utilisée par les architectes afin de définir l'agencement et les proportions des différentes pièces d'un logement.
- Le nombre de pétales de la marguerite (et d'autres fleurs composées comme le tournesol) appartient à la suite de Fibonacci : souvent 34, 55 ou 89. Cela s'explique par le mécanisme de développement de la plante. Voir ici une explication et le lien avec le nombre d'or dans la nature.
- La plupart des êtres vivants sexués sont issus de deux parents, de sorte que leurs ancêtres à la ne génération, supposés distincts, sont au nombre de 2n. Mais les hyménoptères sont tels que les femelles sont issues de deux parents, et les mâles sont issus d'une mère seulement. Il en résulte que leurs ancêtres à la ne génération sont constitués :
-
- pour les femelles, de
 mâles et
mâles et  femelles,
femelles, - pour les mâles, de
 mâles et
mâles et  femelles.
femelles.
- pour les femelles, de
DémonstrationPar récurrence sur N que l'on considéra comme la longueur horizontale du rectangle 2×N :
- Initialisation :
- Le rectangle 2×1 est un domino 2×1 ; il y a 1 seule façon de paver ce rectangle
 .
.
- Le rectangle 2×1 est un domino 2×1 ; il y a 1 seule façon de paver ce rectangle
- Supposons qu'il y ait
 façons de paver le rectangle 2×N.
façons de paver le rectangle 2×N. - Considérons le rectangle 2×(N+1) :
- Ce rectangle 2×(N+1) peut être construit comme la juxtaposition d'un rectangle 2×(N-1) et de 2 dominos placés horizontalement (la longueur du rectangle d'origine est toujours N+1) ; il y a par hypothèse
 façons de paver le rectangle auquel on a retiré les 2 dominos.
façons de paver le rectangle auquel on a retiré les 2 dominos. - Ce rectangle 2×(N+1) peut aussi être construit comme la juxtaposition d'un rectangle 2×N et d'un domino placé verticalement (la longueur du rectangle d'origine est toujours N+1) ; il y a par hypothèse
 façons de paver le rectangle auquel on a retiré le domino.
façons de paver le rectangle auquel on a retiré le domino. - Le nombre de façons de paver le rectangle 2×(N+1) est donc la somme
 , ce qui termine le raisonnement par récurrence.
, ce qui termine le raisonnement par récurrence.
- Ce rectangle 2×(N+1) peut être construit comme la juxtaposition d'un rectangle 2×(N-1) et de 2 dominos placés horizontalement (la longueur du rectangle d'origine est toujours N+1) ; il y a par hypothèse
Généralisations
Il existe plusieurs voies pour généraliser la suite de Fibonacci : on peut modifier les valeurs initiales, modifier les coefficients de la relation de récurrence ou modifier le nombre de termes (ou ordre) de la relation de récurrence.
Suites de Fibonacci généralisées
On appelle suite de Fibonacci généralisée toute suite définie par la même relation de récurrence que la suite de Fibonacci, mais dont les termes initiaux sont différents de 0 et 1. Sur le modèle de la démonstration donnée plus haut (voir section Expression fonctionnelle), une telle suite un est encore de la forme αφn + βφ'n où φ est le nombre d'or et φ' = − 1 / φ. Elle est donc équivalente à αφn, si bien que (comme la suite des quotients de la suite de Fibonacci) la suite
 converge vers φ.
converge vers φ.Parmi ces suites de nombres, il faut signaler les nombres de Lucas obtenus en choisissant comme initialisation :
 et
et  . Cela donne la suite 2, 1, 3, 4, 7, 11, 18, 29, … On trouve parfois une initialisation
. Cela donne la suite 2, 1, 3, 4, 7, 11, 18, 29, … On trouve parfois une initialisation  et
et  qui ne consiste qu'à décaler la suite d'un rang. Ces nombres interviennent dans la résolution d'équations diophantiennes. Ils sont très liés à la suite de Fibonacci, en particulier par la relation suivante :
qui ne consiste qu'à décaler la suite d'un rang. Ces nombres interviennent dans la résolution d'équations diophantiennes. Ils sont très liés à la suite de Fibonacci, en particulier par la relation suivante :  pour tout entier n strictement positif (voir Propriétés, Propriété 9).
pour tout entier n strictement positif (voir Propriétés, Propriété 9).Suites de Lucas
Ce sont les suites où la relation de récurrence a changé : elle est devenue
Elles sont de deux types selon que l'initialisation est de u0 = 0 et u1 = 1 ou qu'elle est v0 = 2 et v1 = P.
La suite de Fibonacci est alors une suite u de Lucas de paramètres P = 1 et Q = 1. La suite des nombres de Lucas est alors une suite v de Lucas de paramètres P = 1 et Q = 1.
Articles détaillés : Suite de Lucas et Nombre de Lucas.Suites de k-bonacci
Ce sont des suites dont la relation de récurrence est d'ordre k. Un terme est la somme des k termes qui le précèdent
Parmi ces suites, on distingue la suite de Tribonacci (récurrence d'ordre 3) et la suite de Tetranacci (récurrence d'ordre 4). Selon ce nouveau classement de suites, la suite de Fibonacci est une suite de 2-bonacci.
Si on modifie tout à la fois (initialisation, récurrence, ordre) on arrive à l'ensemble très général des suites à récurrence linéaire.
La suite de Fibonacci dans la culture populaire
Littérature
- Da Vinci Code, de Dan Brown
- Maya Fox 2012, tome 1 : La prédestinée, de Silvia Brena et Iginio Straffi (it)
- La Confrérie des Invisibles, de Kurt Aust (en)
- Le problème avec les lapins, d'Emily Gravett
- Les Pyramides de Napoléon, de William Dietrich
Cinéma
Télévision
- Numb3rs (épisodes 6, 21 des saison 1, 5)
- Fringe (épisode 10 de la saison 1)
- Chuck (épisode 7 de la saison 2)
- Alias
- Lost
- Esprits Criminels (épisode 8 de la saison 4)
- Disparition
Musique
Le groupe de metal progressif Tool structure le rythme de certaines parties du morceau Lateralus selon une suite de Fibonacci[6].
Architecture
Le Corbusier et son Modulor, une mesure harmonique à l'échelle humaine applicable universellement à l'Architecture et à la mécanique.
Notes et références
- (la) J. Kepler, Strena seu de nive sexangula, 1611
- (en) Paulo Ribenboim, The New Book of Prime Number Records, New York, Springer, 1996 (ISBN 0-387-94457-5), p. 64
- (en) Franz Lemmermeyer (de), Reciprocity Laws, New York, Springer, 2000 (ISBN 3-540-66957-4), ex. 2.25–2.28, p. 73–74
- (en) Fibonacci Number, sur le site Prime Pages
- suite A001605 de l’OEIS
- (en)Christopher diCarlo, Interview with Maynard James Keenan
Voir aussi
Bibliographie
N. Vorobiev, Caractères de Divisibilité, Suite de Fibonacci, coll. Initiation aux Mathématiques, Editions Mir, Moscou, 1973
Articles connexes
- Groupe de Fibonacci
- Suite de Padovan
- Nombre d'or
- Mot de Fibonacci
- Polynôme de Fibonacci (en)
- Codage de Fibonacci
- The Fibonacci Association (en) et sa revue, Fibonacci Quarterly
Liens externes
Wikimedia Foundation. 2010.

























 et
et  sont premiers entre eux (ils n'ont aucun
sont premiers entre eux (ils n'ont aucun  n'est pas
n'est pas 







