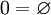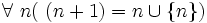- Fondements Des Mathématiques
-
Fondements des mathématiques
Le problème de la fondation ou des fondements, des mathématiques est celui des principes sur lequel est établie cette science, de sa vérité et de son contenu. Il s'agit en particulier de répondre à la question : « À partir de quels principes les connaissances mathématiques se développent-elles ? »
Sommaire
Le problème des fondements des mathématiques
Les mathématiques, ensemble des sciences ayant pour objet le nombre, la quantité, l’étendue et l’ordre, constituent apparemment le modèle de toute science. Avec les Grecs, les mathématiques changent de statut : elles passent des calculs empiriques aux démonstrations rationnelles ; un détachement par rapport aux objets particuliers s’opère ; le concept de démonstration s’élabore avec le développement des maths. Avec Galilée, les mathématiques sont appliquées systématiquement à la physique, d’où le renforcement du prestige de cette science.
Il est possible de mettre en évidence trois caractéristiques des mathématiques :
- Les mathématiques constituent un corpus de démonstrations rigoureuses : le passage d’un chaînon au suivant est censé ne laisser aucune place au doute et emporte par là l’assentiment universel.
- Elles utilisent un langage univoque, artificiel et conventionnel, afin d’échapper aux confusions sous-tendues par le langage ordinaire.
- Par principe, les mathématiques sont une science hypothético-déductive : tout ce qui est établi procède d’enchaînements déductifs ; un théorème est une proposition dont la démonstration est possible par déductions successives. Ces chaînes déductives s’enracinent dans des vérités posées par hypothèse. Ces vérités sont les postulats, les axiomes et les définitions.
Dès lors, si l’on considère, du point de vue épistémologique, le réseau de croyances – ou attitudes propositionnelles d’un agent – constitutif des mathématiques, celui-ci renvoie à deux modèles distincts de la connaissance : le modèle fondationaliste et le modèle cohérentiste.
Le modèle fondationaliste repose sur la distinction entre les croyances de base (ou fondationnelles) et les croyances dérivées. L’enjeu du fondationalisme est de répondre au problème spécifique suivant : « Comment établir les croyances de base ? » Les propriétés épistémiques des croyances dérivées relèvent en effet de celles des croyances de base. Les croyances de base sont des points terminaux dans une chaîne des raisons ; elles sont immunisées à l’égard du doute.
Selon le modèle cohérentiste, d’autre part, toutes les croyances propositionnelles ont prima facie, le même statut épistémologique. Les propriétés épistémiques d’une croyance propositionnelle donnée dépendent des propriétés épistémiques, non seulement d’autres croyances propositionnelles qui la justifient, mais encore, du réseau de croyances dans son ensemble. Les croyances propositionnelles n’ont aucune propriété intrinsèque, permettant d’opérer une distinction entre croyance de base et croyance dérivée. Toute croyance est par conséquent, sujette à révision ou pour le moins, révisable.
Ainsi, dans le cas du théorème, la vérité est donnée par préservation : étant donné les prémisses du raisonnement et la vérité de ces prémisses, la vérité du théorème est établie. La propagation de la vérité à travers le système relève de procédés essentiellement d’ordre syntaxique. Ce type de proposition peut être appelée : C-propositions (propositions cohérentes), c’est-à-dire des propositions dont la valeur de vérité est obtenue par préservation. D’autre part, la vérité des axiomes résulte d’un autre type d’attribution : elle est déclarée. Le procédé de déclaration de la vérité ne signifie rien d’autre que ceci : ce qui rend vrai un axiome ne trouve aucune expression dans les limites du langage formel donné. Il n’est pas nécessaire d’interroger les axiomes sur leurs origines. Les motifs et les justifications pour accepter la vérité d’une proposition à titre d’axiome ne sont pas pertinents. Seul compte le fait de déclarer la vérité de la proposition. Ce type de propositions peut être appelé : F-propositions (propositions fondationnelles), c’est-à-dire une proposition dont la valeur de vérité est obtenue par déclaration. Alors que les C-propositions permettent de propager et de garantir la consistance, les F-propositions introduisent la vérité dans le système.
De là, il s’ensuit une interrogation permanente au sujet des fondements des mathématiques : quelle est la solidité des F-propositions ? Ne sont-elles pas de simples suppositions ? Trois conceptions s’opposent par rapport au problème des fondements des mathématiques :
Le logicisme
Le logicisme a été prôné notamment par Gottlob Frege et Bertrand Russell. La mathématique pure présente deux caractéristiques : la généralité de son discours –- la considération des particuliers existants est exclue -- et la déductibilité du discours mathématique –- les inférences qui structurent le discours mathématique sont des implications formelles (elles affirment non pas les propositions elles-mêmes, mais la nécessité de leur connexion) --. En ce que le discours mathématique ne prétend qu’à une vérité formelle, il est possible de réduire les mathématiques à la logique, les lois logiques étant les lois du « vrai ». Par exemple, la définition logique du nombre, loin d’être réduite à l’opération concrète de dénombrement d’objets, consiste en la référence à l’égalité numérique de deux classes (deux classes ont le même nombre s’il est possible d’instaurer entre leurs éléments respectifs une relation bijective). Le logicisme a rencontré néanmoins, à ses débuts, de réelles difficultés en tant qu’il s'engage ontologiquement par rapport aux classes. Or, la théorie des classes a conduit à des paradoxes logiques.
Le formalisme
Le formalisme soutenu par David Hilbert : les mathématiques se présentent comme une pure construction de l’esprit. La tâche des mathématiciens est de déduire des théorèmes à partir d’axiomes qui ne sont ni vrais ni faux. La validité ne repose plus que sur la structure des énoncés, et non sur la nature de ce dont ils parlent. La vérité des mathématiques est réduite à leur cohérence interne, la non contradiction des propositions. Le débat sur cette conception formaliste a été relancé par le théorème d'incomplétude de Gödel qui affirme que tout système formel cohérent et récursif contenant l'arithmétique, possède une proposition valide (ou disons « vraie ») qui n’est ni démontrable, ni réfutable.
L'intuitionnisme
L’intuitionnisme défendu de manière paradigmatique par Brouwer : les mathématiques ont un fondement intuitif. Sans l’intuition, la logique s’avère stérile. Défendre une conception intuitionniste a des conséquences importantes. Ainsi, selon la logique intuitionniste, on ne peut pas éliminer la double négation (ce que fait la logique classique) : « non non p » ne se réduit pas à « p ». Il s’ensuit que « non p ou p » n'est pas un théorème. Ces refus sont justifiés par le fait qu'en logique intuitioniste « q implique r » signifie que « d'une démonstration de q je peux construire une démonstration de r », or l'affirmation « non non p implique p» ne permet pas de construire une démonstration de p à partir d'une démonstration de « non non p ».
Les fondements de la géométrie
L’œuvre de Hilbert est très représentative de la crise des fondements qui s’est produite en mathématiques pendant le XIXe et au début du XXe siècle.
Hilbert, comme d’autres logiciens et mathématiciens de son temps, s’est rendu compte que la géométrie euclidienne était incomplète, pas au sens où l’axiome des parallèles n’y est pas déductible, mais parce que tous les géomètres depuis Euclide se servent dans leurs preuves d’axiomes qui n’avaient jamais été explicités. À la suite des travaux de Pasch, Hilbert a donné une formulation presque complète de la géométrie euclidienne, dans son livre Les Fondements de la géométrie, pour laquelle aucun axiome géométrique n’était laissé dans l’ombre.
Ce programme de fondation de la géométrie n’était cependant pas achevé pour deux raisons. D’une part, les règles de raisonnement admises étaient encore laissées dans l’ombre. D’autre part, un des axiomes de la géométrie, relatif à la continuité de l’espace, posait des problèmes d’interprétation associés à ceux de la définition des nombres réels et de la théorie des ensembles de Cantor.
Les fondements de l’analyse et la théorie des ensembles
L’analyse, que l’on peut aussi appeler calcul infinitésimal, ou calcul différentiel et intégral, repose maintenant sur la définition de l’ensemble des nombres réels. Depuis les découvertes de Newton et Leibniz, il avait fallu sortir du cadre des Éléments d'Euclide.
Les mathématiciens du XIXe siècle, notamment Cauchy et Weierstrass, pour l'analyse proprement dite, puis Dedekind et Cantor ont donné une formulation précise de principes qui permettent de raisonner avec rigueur et exactitude sur les nombres réels. Ceux-ci sont définis par Dedekind comme des ensembles de nombres rationnels. Peano a donné des axiomes et des méthodes formelles pour développer d’une façon logiquement rigoureuse l’arithmétique et celle-ci suffit pour fonder la théorie des nombres rationnels.
La théorie des ensembles de Cantor, qui n'était pas vraiment formalisée, semblait cependant le cadre idéal, paradisiaque selon l’expression de Hilbert, pour fonder l’analyse et plus généralement les mathématiques. Frege, de son côté avait donné des règles formelles précises et explicites pour une théorie logique qui devait permettre de fonder les mathématiques. On pouvait espérer une base solide.
Mais cette base n'a pas tardé à montrer ses faiblesses. La découverte du paradoxe de Burali-Forti (l'ensemble de tous les ordinaux est bien ordonné, ce bon ordre est supérieur à tous les ordinaux, donc à son propre ordinal), puis celle du paradoxe de Russell, proche sur le principe mais nettement plus simple (l'ensemble des ensembles qui ne s'appartiennent pas à eux-mêmes est un ensemble, il ne peut ni s'appartenir, ni ne pas s'appartenir à lui-même), montrent l'incohérence des ces deux théories (Russell a donné son paradoxe initialement pour la théorie de Frege).
Des solutions pour éviter ces paradoxes furent rapidement trouvées. L'une, initiée par Russell, et développée dans les Principia Mathematica, stratifie les prédicats grâce à la notion de type : on ne peut plus écrire qu'un ensemble appartient à lui-même. L'autre, initiée par Zermelo, restreint la définition des ensembles par compréhension, c'est-à-dire par une propriété de ses éléments : la propriété de ne pas appartenir à soi-même ne définit plus un ensemble.
Mais pouvait-on s'assurer que l'on ne puisse pas dériver de nouveaux paradoxes dans ces théories ?
Le programme de Hilbert
Pour répondre à la crise des fondements des mathématiques, Hilbert avait conçu un programme dont il établit les prémisses en 1900 dans l'introduction à sa célèbre liste de problèmes, le second problème étant justement celui de la cohérence de l'arithmétique. Il développe ce programme avec ses collaborateurs, parmi lesquels Bernays et Ackermann, essentiellement dans les années 1920. L'idée est grossièrement la suivante.
Tant que l'on manipule le fini, les mathématiques sont sûres. L'arithmétique élémentaire (en un sens qui doit se préciser) est sûre. Pour justifier l'utilisation d'objets abstraits ou idéaux, en particulier infinis, il suffit de montrer que la théorie qui les utilise est cohérente, mais bien-sûr cette cohérence doit elle-même être démontrée par des moyens finitaires. On peut alors affirmer l'existence de ces objets. C'est la position formaliste (à ne pas confondre avec le finitisme qui considère que seules les constructions directement finitaires ont un sens).
Le système dans lequel on pourrait formaliser les mathématiques finitaires n'est pas clair. À l'époque, il semble que Hilbert pensait, sans l'avoir explicitement formalisé, à un système plus faible que l'arithmétique de Peano, l'arithmétique primitive récursive : toutes les définitions de fonctions récursives primitives sont dans le langage, la récurrence est restreinte aux formules sans quantificateurs (disons aux égalités pour faire simple), donc très immédiate. Peu importe en fait : le second théorème d'incomplétude de Gödel, montre que l'on ne pourra même pas prouver dans la théorie arithmétique en question sa propre cohérence, et donc certainement pas celle de théories plus fortes qui assureraient la fondation des mathématiques.
Le programme de Hilbert n'est donc pas réalisable, en tout cas pas sans une révision drastique. Des logiciens comme Gentzen, et Gödel lui-même, ont pensé à rétablir ce programme en étendant la notion de méthodes finitaires, celles-ci ne pouvant cependant pas être définies une fois pour toutes par une théorie toujours à cause du second théorème d'incomplétude. Ainsi Gentzen a donnée en 1936 une preuve de cohérence de l'arithmétique de Peano dans un système forcément plus fort, où l'on raisonne par induction sur un ordre bien fondé (dénombrable mais plus grand que l'ordre des entiers), mais où l'induction est cependant restreinte à des formules sans quantificateurs, donc plus "immédiate". Si l'intérêt mathématique des méthodes mise en œuvre par Gentzen ne fait aucun doute, l'interprétation de ses preuves de cohérence, en tant que preuves "absolues" (ce sont bien sûr indubitablement des preuves de cohérence relative) reste très discutable.
Il reste que, malgré son échec, le programme de Hilbert a joué un rôle décisif dans le développement de la logique mathématique moderne.
La méthode formelle
Il ne faudrait pas confondre formalisme, et méthode formelle. La méthode formelle est essentielle pour comprendre les mathématiques contemporaines.
Définir une théorie formelle, c'est :
- se donner des symboles (a, b, c, =, +, ≥ etc<;) ;
- se donner une syntaxe pour construire des « phrases ». Par exemple on peut écrire a≥b mais pas a b ≥ ;
- se donner une méthode pour déduire des phrases à partir d'autres phrases. Par exemple, si on a a≥b et b≥c alors on a aussi la « phrase » a≥c.
Définir une théorie de façon formelle est essentiel pour en donner des propriétés : cohérence ou incohérence, complétude ou incomplétude etc. Tant qu’on a pas formalisé une théorie, on ne sait pas exactement si une formule appartient ou non à la théorie.
Les règles de déduction de la logique traditionnelle sont désormais complètement connues et formalisées au sein de la logique mathématique. Toutes les connaissances mathématiques peuvent être prouvées avec ces règles et des axiomes convenablement choisis.
C'est probablement dans cette catégorie que l'on doit classer les mathématiques à rebours d'Harvey Friedman.
Les théories des ensembles
Les mathématiques actuelles sont basées sur la notion d' ensemble. En fait, tout objet mathématique ou presque peut être défini comme un ensemble. Par exemple, « 23 » peut être défini comme un ensemble qui contient 23 éléments.
De même,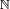 peut être construit à partir d'ensembles comme suit :
peut être construit à partir d'ensembles comme suit :(voir à ce sujet l'article sur la construction des entiers naturels).
Avec de telles définitions, ou d’autres semblables, toutes les connaissances mathématiques peuvent être prouvées à l’intérieur d’une théorie des ensembles. Leurs axiomes peuvent être considérés comme les principaux fondements des mathématiques (avec les règles de déduction du calcul des prédicats au premier ordre).
Plusieurs systèmes d’axiomes ont été proposés :
- La théorie axiomatique des ensembles « standard » comporte neuf axiomes. Ces axiomes ont été énoncés par Zermelo (1908) et complétés dans les années 1920 par Fraenkel et Skolem. Ils sont dits de Zermelo-Fraenkel et comprennent l'axiome du choix, d'où le sigle ZFC souvent employé pour désigner cette théorie. L'œuvre de l'association Bourbaki a été développée dans ce cadre axiomatique.
- La théorie des classes, de von Neumann, Gödel et Bernays (NGB). C’est une extension de ZFC qui lui est presque équivalente. Tous les théorèmes de ZFC sont des théorèmes de NGB. Inversement, tous les théorèmes de NGB qui ne mentionnent que les notions fondamentales de ZFC (c’est-à-dire les ensembles et non les classes) sont des théorèmes de ZFC. NGB convient mieux que ZFC pour formuler la théorie des catégories.
- La théorie des types de Whitehead et Russell, exposée principalement dans les Principia Mathematica. Son formalisme est lourd (des dizaines de pages pour prouver des propositions qui nous paraissent au premier abord évidentes) et ses principes sont peu élégants, parce qu’ils imposent beaucoup d’interdits. Outre sa grande importance historique parce qu’elle est la première formulation axiomatique, rigoureuse et cohérente des principes généraux des mathématiques, elle a, grâce à l'informatique, repris de la vigueur à la fin du siècle précédent et au début de celui-ci et devient une discipline phare de la logique mathématique contemporaine.
- La théorie du zig-zag interdit de Quine. Elle n'est pas très utilisée mais pourrait l’être davantage. Elle montre en particulier qu’on peut développer une théorie des ensembles sans exclure l’ensemble de tous les ensembles.
- D’autres théories, qui sont soit moins puissantes que les précédentes, parce qu’elles refusent les constructions ensemblistes trop audacieuses (théories constructivistes, intuitionnistes, finitaires, ...), soit plus puissantes parce qu’elles les complètent avec d’autres axiomes (axiome de constructibilité, axiomes des très grands ensembles, ...)
Parmi les mathématiciens, certains se contentent des axiomes ZF, et refusent l'axiome du choix (C), car ils considèrent que certaines de ses implications sont contre-intuitives. Certains mathématiciens refusent même ZF et la logique classique qui en est la base, car ils considèrent que tout doit être construit explicitement; c'est la raison pour laquelle on les appelle constructivistes ou intuitionnistes.
L'analyse non-standard est aussi une voie qui remet en cause certains principes fondamentaux des mathématiques.
Voir aussi
Références
- Conférence sur les fondements des mathématiques, par Jean-Yves Girard, 17 juin 2002, Université de tous les savoirs.
- Portail de la logique
- Portail des mathématiques
Catégories : Philosophie des mathématiques | Fondements des mathématiques | Logique
Wikimedia Foundation. 2010.