- Logique Intuitionniste
-
Logique intuitionniste
L'intuitionnisme est une position philosophique vis-à-vis des mathématiques proposée par le mathématicien hollandais Luitzen Egbertus Jan Brouwer comme une alternative à l'approche dite classique. Elle a été ensuite formalisée, sous le nom de logique intuitionniste, par ses élèves V. Glivenko et A.Heyting. Kurt Gödel a montré que l'on pouvait représenter la logique classique dans la logique intuitionniste, corroborant le fait que la logique intuitionniste n'est pas une logique à part, mais fait bien partie de la Logique. Gerhard Gentzen en a formalisé les règles de déduction dans le cadre de la déduction naturelle.
Les travaux récents, notamment la correspondance de Curry-Howard, lui ont donné un statut central dans la logique et dans l'informatique, en en faisant historiquement la première des logiques constructives. L'étude de la logique intuitionniste est la clé pour bien comprendre la logique classique et ses subtilités.
Sommaire
Approche informelle
Brouwer a fondé l'intuitionnisme comme une position philosophique vis-à-vis des mathématiques ; cela l'a conduit à rejeter certaines formes du raisonnement mathématique traditionnel, qu'il jugeait contre-intuitives. En fait, il refusait deux concepts.
- Le tiers exclu, qui consiste à dire qu'étant donnée une proposition φ, soit on a φ, soit on a non(φ), formellement
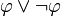 . A titre d'exemple, il rejetait la démonstration suivante de la proposition : « Il existe des nombres irrationnels a et b, tels que ab est un nombre rationnel» :
. A titre d'exemple, il rejetait la démonstration suivante de la proposition : « Il existe des nombres irrationnels a et b, tels que ab est un nombre rationnel» :
« Si
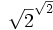 est rationnel,
est rationnel, 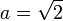 et
et 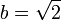 conviennent. Sinon, prenons
conviennent. Sinon, prenons 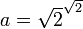 et
et 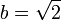 . Nous avons
. Nous avons 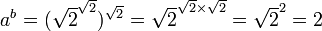 qui donne le résultat puisque 2 est évidemment rationnel ». La critique de cette démonstration est qu'elle utilise le tiers exclu et qu'elle n'exhibe pas un couple particulier qui serait solution. En fait, un théorème d'analyse affirme que
qui donne le résultat puisque 2 est évidemment rationnel ». La critique de cette démonstration est qu'elle utilise le tiers exclu et qu'elle n'exhibe pas un couple particulier qui serait solution. En fait, un théorème d'analyse affirme que 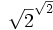 est irrationnel et que c'est le a qu'il faut choisir, mais la démonstration fondée sur le tiers exclu ne le dit pas.
est irrationnel et que c'est le a qu'il faut choisir, mais la démonstration fondée sur le tiers exclu ne le dit pas.- L'existentiel non constructif. Brouwer veut que quand un mathématicien affirme il existe x tel que x est P, que l'on écrirait formellement
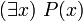 , il donne aussi un moyen de construire x qui satisfait P.
, il donne aussi un moyen de construire x qui satisfait P.
Brouwer a prôné une mathématique qui rejetterait le tiers exclu et n'accepterait que l'existentiel constructif. Cette attitude a été assez violemment critiquée par des mathématiciens comme David Hilbert tandis que d'autres comme Hermann Weyl y ont souscrit. Une fois formalisée, trois faits font de la logique intuitionniste une logique à part entière : l'existence de modèles qui font d'elle un système complet de déduction, la découverte de son contenu calculatoire, connu sous le nom de correspondance de Curry-Howard, enfin le fait qu'elle est une logique modale. La logique intuitionniste n'a donc rien d'exotique. Allant plus loin, le logicien Jean-Yves Girard a proposé une logique plus faible que la logique intuitionniste, qu'il a appelée la logique linéaire, qui se trouve à la base de toute logique et qui permet de mieux comprendre la logique intuitionniste en particulier.
La logique intuitionniste revisite aussi le concept d'implication. L'implication
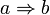 n'est plus l'implication matérielle
n'est plus l'implication matérielle 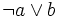 . Quand un mathématicien intuitionniste affirme
. Quand un mathématicien intuitionniste affirme 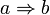 , il veut dire qu'il fournit un procédé de « construction » d'une démonstration de
, il veut dire qu'il fournit un procédé de « construction » d'une démonstration de 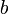 à partir d'une démonstration de
à partir d'une démonstration de 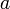 . Ceci est d'ailleurs la clé du contenu calculatoire de la logique intuitionniste.
. Ceci est d'ailleurs la clé du contenu calculatoire de la logique intuitionniste.Approche formelle
Nous venons de voir que l'implication et la disjonction ne sont plus liées. Mais en fait cela va plus loin: une des caractéristiques de la logique intuitionniste est le fait que chaque connecteur (
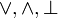 ) et chaque quantificateur (
) et chaque quantificateur (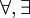 ) doit être défini à partir de ses propres règles, autrement dit il n'y a pas de moyen de ramener la logique à un connecteur et à un quantificateur. C'est pourquoi nous allons donner des règles pour chaque connecteur.
) doit être défini à partir de ses propres règles, autrement dit il n'y a pas de moyen de ramener la logique à un connecteur et à un quantificateur. C'est pourquoi nous allons donner des règles pour chaque connecteur.La logique implicative minimale
Pour introduire la logique intuitionniste, le plus simple est de commencer par la déduction naturelle en logique implicative minimale, qui est la logique propositionnelle dans laquelle il n'y a qu'un connecteur, l'implication
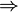 .
.Rappelons qu'en déduction naturelle
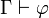 doit se lire « de l'ensemble de propositions
doit se lire « de l'ensemble de propositions 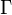 on déduit la proposition
on déduit la proposition 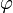 ».
».Il y a alors deux règles (voir plus bas Lecture des règles) :
 .
.La première régle s'appelle la règle d'élimination de l'implication, tandis que la seconde règle s'appelle la règle d'introduction de l'implication. On remarque que l'élimination de l'implication est aussi le modus ponens bien connu. La méthode qui consiste à avoir pour chaque connecteur une (ou des) règle(s) d'élimination et une (ou des) règle(s) d'introduction est typique de la déduction naturelle et nous allons la retrouver par la suite.
Ce système de déduction est très simple (rasoir d'Ockham), mais il est moins puissant que la logique classique, car on ne peut y démontrer ni la loi de Peirce
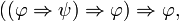 ni la proposition
ni la proposition 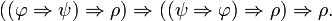
Lecture des règles
La règle d'élimination de l'implication peut se lire comme suit : si de l'ensemble d'hypothèses Γ je déduis
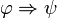 et si de plus de l'ensemble d'hypothèses Γ je déduis
et si de plus de l'ensemble d'hypothèses Γ je déduis 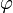 alors de l'ensemble d'hypothèses Γ je déduis ψ. Nous verrons (section interprétation de la logique intuitionniste) que l'expression « je déduis » prend un sens plus fort en logique intuitionniste qu'en logique classique. La règle d'introduction de l'implication, quant à elle, peut se lire comme suit : si de l'ensemble d'hypothèses Γ et de l'hypothèse
alors de l'ensemble d'hypothèses Γ je déduis ψ. Nous verrons (section interprétation de la logique intuitionniste) que l'expression « je déduis » prend un sens plus fort en logique intuitionniste qu'en logique classique. La règle d'introduction de l'implication, quant à elle, peut se lire comme suit : si de l'ensemble d'hypothèses Γ et de l'hypothèse 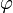 je déduis ψ alors de l'ensemble d'hypothèses Γ je déduis
je déduis ψ alors de l'ensemble d'hypothèses Γ je déduis 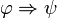 .
.La logique propositionnelle intuitionniste
On conserve les règles de la logique implicative minimale concernant l'implication.
L'absurde
L'absurde est la proposition, notée
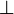 , qui traduit une proposition essentiellement fausse. Elle est régie par une règle:
, qui traduit une proposition essentiellement fausse. Elle est régie par une règle: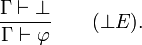
Cela signifie que si un ensemble de propositions Γ conduit à l'absurde, alors de cet ensemble de propositions Γ, je peux déduire n'importe quelle proposition
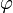 .
.Cette règle est aussi la règle d'élimination de l'absurde. Il n'y a pas (heureusement!) de règle d'introduction de l'absurde. Le nom de cette règle ne doit pas la faire confondre avec la règle de raisonnement par l'absurde (reductio ad absurdum) qui n'existe pas en logique intuitionniste. En effet le raisonnement par l'absurde est étroitement lié au tiers exclu et n'est pas constructif.
Remarque: en logique classique cette règle n'est pas utile, car elle est une conséquence du raisonnement par l'absurde.
La négation
Traditionnellement, on considère la négation comme une abréviation. Plus précisément on dit que
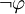 est en fait une abréviation pour
est en fait une abréviation pour 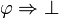 . Il n'y a donc pas de règles spécifiques à la négation.
. Il n'y a donc pas de règles spécifiques à la négation.La conjonction
On introduit un nouveau connecteur binaire
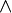 , representant la conjonction de deux formules. On lit
, representant la conjonction de deux formules. On lit 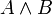 : A et B. On lui associe deux régles d'élimination,
: A et B. On lui associe deux régles d'élimination, 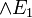 et
et 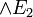 , et une régle d'introduction.
, et une régle d'introduction.
La disjonction
On introduit un nouveau connecteur binaire
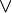 , representant la disjonction de deux formules. Il est en quelque sorte symétrique du connecteur
, representant la disjonction de deux formules. Il est en quelque sorte symétrique du connecteur 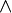 . Ainsi, on lui associe une régle d'élimination et deux régles d'introduction.
. Ainsi, on lui associe une régle d'élimination et deux régles d'introduction.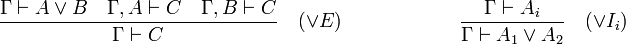
On remarque que la règle d'élimination de la disjonction est une règle tryadique, c'est-à-dire qu'elle a trois prémisses.
Le calcul des prédicats intuitionniste
Interprétation de la logique intuitionniste
Approche intuitive
La logique intutionniste peut être vue comme une logique modale, munie de la modalité de nécessité, notée
 où l'implication intuitionniste est
où l'implication intuitionniste est 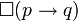 , quand
, quand 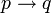 est l'implication classique. Cela peut se lire nécessairement p implique q. L'idée des modèles de Kripke est de créer une hiérarchie qui donne de plus en plus de « nécessité» aux implications. Comme cela ne concerne que l'implication intuitionniste, il n'y a qu'elle qui sera concernée par cette hiérarchie.
est l'implication classique. Cela peut se lire nécessairement p implique q. L'idée des modèles de Kripke est de créer une hiérarchie qui donne de plus en plus de « nécessité» aux implications. Comme cela ne concerne que l'implication intuitionniste, il n'y a qu'elle qui sera concernée par cette hiérarchie.La sémantique de la logique intuitionniste est fondée sur les modèles de Kripke. Ces modèles sont eux-mêmes fondés sur des mondes dans lesquels opèrent la sémantique classique (en 0 et 1 pour le calcul des propositions). Ces mondes peuvent être vus comme des contenus d'information de plus en plus riches. Ils sont donc hiérachisés par une relation d'ordre (la relation d'accessibilité). Si une proposition est « satisfaite » dans un monde, on dit que ce monde force la proposition. Un monde force une proposition
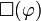 , si tous les mondes qui le dominent hiérarchiquement forcent
, si tous les mondes qui le dominent hiérarchiquement forcent 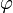 . Comme la nécessité ne va être appliquée qu'à l'implication, nous dirons qu'un monde force
. Comme la nécessité ne va être appliquée qu'à l'implication, nous dirons qu'un monde force 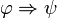 si pour tous les mondes m qui le dominent hiérarchiquement, on a m force ψ dès que m force
si pour tous les mondes m qui le dominent hiérarchiquement, on a m force ψ dès que m force 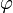 .
.On dira qu'un modèle de Kripke satisfait ou modèlise une proposition si tous les mondes qu'il contient forcent cette proposition.
Une proposition est valide, si elle est satisfaite par tous les modèles.
On peut montrer que la logique intuitionniste est correcte pour les modèles de Kripke, c'est-à-dire que toute proposition prouvable en logique intuitionniste est valide dans les modèles de Kripke.
Or on peut montrer que les propositions suivantes ne sont pas valides pour les modèles de Kripke:
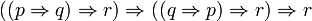 ,
,
On en conclut que ces deux propositions, qui sont pourtant des tautologies classiques, ne sont pas prouvables en logique intuitionniste.
On montre que les modèles de Kripke sont complets pour la logique intuitionniste, c'est-à-dire que toute proposition valide est prouvable.
Approche formelle
Dans cet article nous ne considèrons que les modèles de la logique propositionnelle qui forment un exemple de sémantique de Kripke.
Un modèle est formé d'un triplet
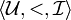 .
.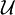 est appelé l'univers et ses éléments notés m sont appelés des mondes,
est appelé l'univers et ses éléments notés m sont appelés des mondes,
- < est une relation d'ordre ,
Un cône est un ensemble C de mondes (
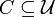 ) tels que
) tels que 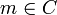 et m < m' impliquent
et m < m' impliquent 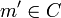 .
.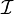 est une initialisation; c'est une application qui associe à chaque variable propositionnelle un cône de
est une initialisation; c'est une application qui associe à chaque variable propositionnelle un cône de 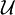 .
.On définit une relation
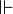 de réalisabilité ou de forçage entre un monde m et une proposition
de réalisabilité ou de forçage entre un monde m et une proposition 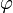 , que l'on écrit
, que l'on écrit 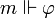 et que l'on lit m force
et que l'on lit m force 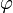 . La relation de forçage est définie par induction sur la structure des formules.
. La relation de forçage est définie par induction sur la structure des formules.- si φ est une variable x, alors
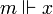 si
si 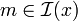 ,
, - si φ est une proposition
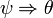 alors
alors 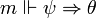 , si pour tout monde m' tel que
, si pour tout monde m' tel que 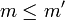 on a si
on a si 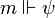 alors
alors 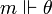 .
.
On peut démontrer (par induction sur la structure ou la taille de
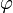 ) que pour chaque proposition
) que pour chaque proposition 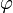 , l'ensemble des m tels que
, l'ensemble des m tels que 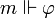 est un cône.
est un cône.On dit que
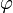 est valide dans
est valide dans 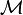 ou que
ou que 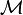 modélise
modélise 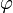 , noté
, noté 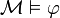 , si pour
, si pour 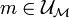 , on a
, on a 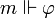 . On dit que
. On dit que 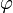 est valide, si pour tout modèle
est valide, si pour tout modèle 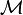 ,
, 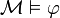 .
.Correction de la logique intuitionniste
On peut montrer que la logique intuitionniste est correcte vis-à-vis des modèles de Kripke, c'est-à-dire que toute proposition démontrable est valide.
Formellement,
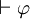 implique
implique 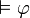 .
.On peut utiliser ce résultat pour montrer qu'une proposition n'est pas démontrable en logique intuitionniste. Si on considère le modèle
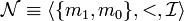 avec m0 < m1 et
avec m0 < m1 et 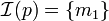 et
et 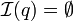 , on peut montrer que
, on peut montrer que 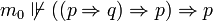 , donc
, donc 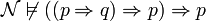 et donc que
et donc que 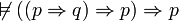 . La loi de Peirce n'est pas valide vis-à-vis des modèles de Kripke, donc elle n'est pas démontrable en logique intuitionniste.
. La loi de Peirce n'est pas valide vis-à-vis des modèles de Kripke, donc elle n'est pas démontrable en logique intuitionniste.On peut aussi trouver un contre-modèle très simple de la proposition
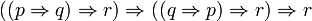 .
.Complétude de la logique intuitionniste
On peut démontrer que toute proposition valide est démontrable.
Formellement,
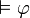 implique
implique 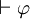 .
.La démonstration se fait de la façon suivante: si
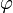 n'est pas démontrable alors on peut construire un contre-modèle (infini) de
n'est pas démontrable alors on peut construire un contre-modèle (infini) de 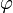 c'est-à-dire un modèle
c'est-à-dire un modèle 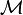 tel que
tel que 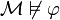 .
.Voir aussi
Références
Articles connexes
- Portail des mathématiques
- Portail de la philosophie
- Portail de la logique
Catégories : Logique | Logique mathématique | Théorie des types | Théorie de la démonstration - Le tiers exclu, qui consiste à dire qu'étant donnée une proposition φ, soit on a φ, soit on a non(φ), formellement
Wikimedia Foundation. 2010.

 (
(