- Composition De Fonctions
-
Composition de fonctions
En mathématiques, la composition de fonctions (ou composition d'applications) est un procédé qui consiste, à partir de deux fonctions, d'en construire une nouvelle. Pour cela on utilise les images de la première fonction comme arguments pour la seconde (à condition que cela ait un sens). On parle alors de fonction composée (ou d'application composée).
Sommaire
Définition formelle
Soient X, Y et Z trois ensembles quelconques. Soient deux fonctions
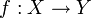 et
et 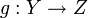 . Si l'ensemble d'arrivée de f est inclus dans l'ensemble de départ de g (c'est-à-dire si
. Si l'ensemble d'arrivée de f est inclus dans l'ensemble de départ de g (c'est-à-dire si 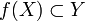 ), on définit alors la composée de f par g, notée
), on définit alors la composée de f par g, notée 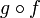 par
parOn applique ici f à l'argument x, puis on applique g au résultat.
On se retrouve donc avec une nouvelle fonction
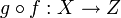 .
.La notation
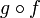 se lit « g rond f », « f suivie de g » ou encore « g après f ». On note parfois
se lit « g rond f », « f suivie de g » ou encore « g après f ». On note parfois 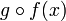 pour
pour 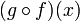 .
.Exemple d'incompatibilité des domaines
Soient les deux fonctions :
et
Ici, le domaine d'arrivée de f est
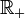 . Or le domaine de départ de g est
. Or le domaine de départ de g est 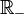 (il n'existe pas de nombre réel tel que son carré soit strictement négatif). La fonction
(il n'existe pas de nombre réel tel que son carré soit strictement négatif). La fonction 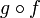 n'a donc pas de sens ici (puisqu'elle n'est vérifiée que pour une seule valeur de x, 0).
n'a donc pas de sens ici (puisqu'elle n'est vérifiée que pour une seule valeur de x, 0).Propriétés
Ici on ne se préoccupe pas des problèmes de compatibilité des domaines des fonctions considérées.
- La composition de fonctions n'est généralement pas commutative :
- La composition de fonctions est associative :
- La composition de fonctions n'est généralement pas distributive (sur un opérateur quelconque
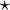 ) :
) :
- Si la fonction g est continue en x0 et la fonction f est continue en g(x0) alors
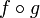 est continue en x0.
est continue en x0.
- Composition de deux fonctions f et g strictement monotones ( le sens de variation obéit à une sorte de règle des signes):
- si f et g ont même sens de variation, leur composée est strictement croissante;
- si f et g ont des sens de variation différents, leur composée est strictement décroissante.
- Dérivée d'une composition de fonctions dérivables :
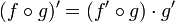
- Voir l'article théorème de dérivation des fonctions composées.
- Réciproque d'une composée :
Puissances fonctionnelles
On conserve les notations ci-dessus. Si
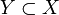 alors f peut être composée avec elle-même; et la composée est notée f2. Ainsi
alors f peut être composée avec elle-même; et la composée est notée f2. AinsiEt de manière plus générale:
On pose
où
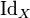 est l'application identité de l'ensemble X.
est l'application identité de l'ensemble X.Une extension de cette notation avec des exposants entiers négatifs peut être définie, à condition de supposer la fonction f bijective de X dans lui-même. Ainsi, f − 1 désigne l'application réciproque et pour tout entier n strictement négatif, fn, est la composée de f − 1 par elle-même − n fois.
Attention à ne pas confondre cette notation avec la puissance d'une fonction pour la multiplication des applications. Par exemple sin2 est la fonction
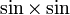 qui vérifie
qui vérifieIl y a aussi une confusion possible entre l'inverse d'une fonction pour la multiplication et l'application réciproque.
Autre notation
Au milieu du XXe siècle, quelques mathématiciens trouvèrent que la notation
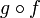 portait à confusion et décidèrent d'utiliser xf pour f(x) et xfg pour
portait à confusion et décidèrent d'utiliser xf pour f(x) et xfg pour 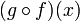 . Ils ne furent pas suivis et cette notation ne se rencontre que dans certains vieux livres.
. Ils ne furent pas suivis et cette notation ne se rencontre que dans certains vieux livres.Voir aussi
- Logique combinatoire
- Lambda calcul
- Fonction d'ordre supérieur
- Théorème de dérivation des fonctions composées
- Portail des mathématiques
Catégories : Opération | Analyse | Mathématiques élémentaires
Wikimedia Foundation. 2010.

![\forall x \in X,\ (g\circ f)(x)=g[f(x)].](/pictures/frwiki/57/925325e8470483b9466ca3355212014c.png)
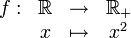
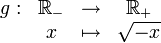
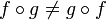
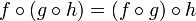
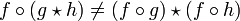
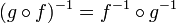
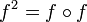
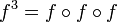
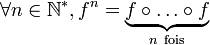
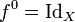
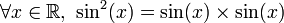

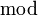
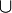
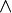
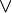
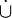
 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe Composition de fonctions
Composition de fonctions
 Cup produit
Cup produit