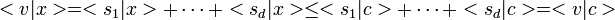- Points et parties remarquables de la frontiere d'un convexe
-
Points et parties remarquables de la frontière d'un convexe
Face à un polyèdre convexe de l'espace de dimension 3, qu'il soit familier comme un cube ou plus exotique, on sait spontanément reconnaître des points où le convexe est « pointu », ses sommets, puis subdiviser les points restants entre points des faces et points des arêtes.
On va ici présenter quelques jeux de définitions qui étendent ces concepts à des ensembles convexes plus généraux, dans n'importe quelle dimension et aux bords possiblement incurvés. Une de ces généralisations, le concept de sommets, est très apparentée à l'intuition qu'on peut avoir de cette notion sur un cube (les points d'une sphère ne seront pas des sommets de la boule qu'elle limite). Les points extrémaux peuvent pour leur être part plus nombreux, suffisamment en fait pour permettre de reconstituer à partir d'eux tout le convexe, et ce même si sa forme est lisse (ainsi dans l'exemple d'une sphère tous les points seront extrémaux).
Après avoir énuméré trois possibles généralisations des sommets d'un cube, l'article fournit deux variantes de la hiérarchie sommets-arêtes-faces, qui ont le bon goût de coïncider dans le cas important des polyèdres convexes.
Sommaire
Les points extrémaux
Définition
Soit C un convexe et c un point de C. On dit que c est un point extrémal de C lorsque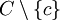 est encore convexe.
est encore convexe.L'ensemble des points extrémaux d'un convexe fermé peut ne pas être fermé, même si l'intuition peut être trompeuse à cause du résultat suivant, qui devient faux à partir de la dimension 3 :
Proposition — Si C est un convexe fermé de dimension 2, l'ensemble de ses points extrémaux est fermé.
Les théorèmes de Minkowski et Krein-Milman
Article détaillé : Théorème de Krein-Milman.Ce théorème, dû à Hermann Minkowski, permet de reconstituer tout le convexe à partir de ses seuls points extrémaux :
Théorème — Tout convexe compact d'un espace affine de dimension finie est enveloppe convexe de l'ensemble de ses points extrémaux.
La démonstration n'est pas très longue, l'outil essentiel étant le théorème d'existence d'un hyperplan d'appui en tout point de la frontière d'un convexe.
Il peut être généralisé à certains espaces de dimension infinie, à condition d'appliquer in fine l'opérateur de fermeture à l'enveloppe convexe. Ce type d'extension à l'analyse fonctionnelle remonte à 1940, et est l'œuvre des mathématiciens Mark Krein et David Milman.
Théorème — Tout convexe compact d'un espace localement convexe séparé est enveloppe convexe l'adhérence de l'ensemble de ses points extrémaux.
Une classe particulière de points extrémaux : les points exposés
Soit C un convexe et c un point de C. On dit que c est un point exposé de C lorsqu'il existe un hyperplan d'appui H de C vérifiant :
 .
.L'énoncé suivant est quasi-évident, mais sa réciproque est fausse, dès la dimension 2 :
Proposition — Tout point exposé est extrémal.
En effet si c est exposé de C, on peut écrire
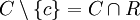 pour R l'un des demi-espaces ouverts délimités par H, d'où la convexité de
pour R l'un des demi-espaces ouverts délimités par H, d'où la convexité de 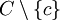 comme intersection de convexes.
comme intersection de convexes.On dispose toutefois, à défaut de réciproque, de l'information suivante (c'est un théorème dû à S. Straszewicz et remontant à 1935) :
Théorème — Dans un convexe fermé en dimension finie, tout point extrémal est limite de points exposés.
Une classe particulière de points exposés : les sommets
Dans cette section, on travaille exclusivement en dimension finie.
Définition et comparaison avec les points exposés
Soit C un convexe et c un point de C. On dit que c est un sommet de C lorsque c est sur la frontière de C et l'intersection des hyperplans d'appui à C au point c est réduite à {c}.
DémonstrationNotons C le convexe, c le sommet considéré, E l'espace affine ambiant et d sa dimension. On munit E d'une structure euclidienne.
Notons Sc la partie de E formée des vecteurs s vérifiant la condition suivante :
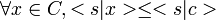 .
.
Lorsque s n'est pas nul cette condition s'interprète géométriquement : elle signifie que l'hyperplan passant par c et perpendiculaire à s est d'appui en c, le vecteur s pointant du côté opposé à celui du convexe. L'intersection des hyperplans d'appui c'est donc l'ensemble des c + u où u est perpendiculaire à tous les éléments de Sc ; en plus concis c'est
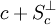 .
.Dire que c est un sommet, c'est dire que cette intersection est réduite à {c}, ce qui revient à dire que
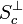 se réduit à {0}, ou encore que l'espace vectoriel engendré par Sc est égal à E tout entier. On peut donc sélectionner un d-uplet de vecteurs (s1,...,sd) dans Sc qui constitue une base de E.
se réduit à {0}, ou encore que l'espace vectoriel engendré par Sc est égal à E tout entier. On peut donc sélectionner un d-uplet de vecteurs (s1,...,sd) dans Sc qui constitue une base de E.Notons
 . Alors pour tout x dans C :
. Alors pour tout x dans C :ce qui prouve déjà que l'hyperplan H passant par x et perpendiculaire à v est d'appui en c ; de plus, si x est un point de
 , l'inégalité qui précède est une égalité. C'est donc nécesairement que toutes les inégalités
, l'inégalité qui précède est une égalité. C'est donc nécesairement que toutes les inégalités 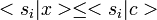 sont elles-mêmes des égalités (
sont elles-mêmes des égalités ( ). Puisque (s1,...,sd) est une base de E, on en déduit que x = c, ce qui prouve que H ne contient aucun point du convexe en dehors de c.
). Puisque (s1,...,sd) est une base de E, on en déduit que x = c, ce qui prouve que H ne contient aucun point du convexe en dehors de c.L'ensemble des sommets est au plus dénombrable
Proposition — Un convexe (en dimension finie) possède un ensemble de sommets au plus dénombrable.
DémonstrationOn reprend les notations introduites à la démonstration précédente.
Remarquons d'abord que pour tous réels strictement positifs α1,...,αd, le vecteur α1s1 + ... + αdsd est dans Sc et que l'ensemble de ces vecteurs est évidemment un ouvert, ce dont on déduit que Sc est d'intérieur non vide. C'est donc aussi le cas de son translaté c + Sc.
Considérons maintenant un vecteur y de c + Sc ; posons y = c + s, avec s dans Sc. Pour x dans C, examinons le produit scalaire
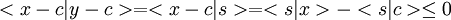 (où l'inégalité finale provient de la définition même de Sc).
(où l'inégalité finale provient de la définition même de Sc).Vu la caractérisation variationnelle de la projection sur un convexe fermé, on en conclut que c est la projection
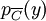 de y sur le convexe fermé
de y sur le convexe fermé 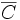 .
.Prenons alors une partie dénombrable dense A de E. Pour tout sommet c du convexe, A rencontre c + Sc (puisque celui-ci est d'intérieur non vide) tandis que
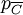 prend la valeur c en tout point de c + Sc : dès lors la restriction de
prend la valeur c en tout point de c + Sc : dès lors la restriction de 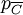 à A prend elle-même la valeur c. Cette application définie sur un ensemble dénombrable prenant tout sommet pour valeur, on conclut alors que l'ensemble des sommets est au plus dénombrable.
à A prend elle-même la valeur c. Cette application définie sur un ensemble dénombrable prenant tout sommet pour valeur, on conclut alors que l'ensemble des sommets est au plus dénombrable.Contextualisations
On prendra garde de ce que le mot « face » n'a pas ici la signification qu'il a dans l'étude des polyèdres traditionnels dans l'espace de dimension 3, celui des éléments plans les bordant. Ici les « faces » vont pouvoir avoir toutes les dimensions, y compris 0 ou 1. Tant les sommets, les arêtes que les « faces » habituelles d'un cube ou d'un tétraèdre seront des faces au sens des définitions qui suivent.
Contextualisation des points exposés : les faces exposées
On va ici commencer par l'extension du concept de « sommets exposés » bien que ce ne soit pas la plus utile, mais parce qu'elle est la plus facile à définir et visualiser : on appelle face exposée d'un convexe C tout ensemble de la forme
 , où H est un hyperplan d'appui de C.
, où H est un hyperplan d'appui de C.La remarque suivante est alors tautologique :
Remarque — Un point c d'un convexe C est exposé si et seulement si {c} est une face exposée de C.
Les faces exposées de C couvrent toute sa frontière puisqu'il passe un hyperplan d'appui au moins en chaque point de celle-ci.
Contextualisation des points extrémaux : les faces
De même que les points exposés sont les faces exposées de dimension zéro, les points extrémaux sont les faces de dimension zéro où « faces » est défini comme suit :
Une partie F d'un convexe C est dite une face de C lorsque F est un convexe non vide ayant la propriété suivante : si un segment ouvert ]x,y[ tracé dans C rencontre F, alors tout le segment fermé [x,y] est inclus dans F.
Les deux énoncés qui suivent sont de vérification quasi-immédiate, le second se vérifiant de la même façon qu'on a vérifié que les points exposés étaient extrémaux :
Proposition — Un point c d'un convexe C est extrémal si et seulement si {c} est une face de C.
Proposition — Les faces exposées sont des faces.
Vu ce deuxième énoncé, les faces de C (autres que C tout entier qui est l'unique face de dimension maximale) couvrent donc toute la frontière de C.
La réciproque n'en est pas vraie (puisqu'il existe des points extrémaux qui ne sont pas exposés, ils donnent aussitôt un exemple de faces qui ne sont pas des faces exposées), avec toutefois une exception pour les faces de codimension 1, qu'on appelle parfois des facettes :
Contrairement aux faces exposées, les faces s'organisent d'une manière hiérarchique particulièrement agréable, comme l'expriment les deux énoncés qui suivent :
Proposition — Si F est une face de C et F1 une face de F, alors F1 est une face de C.
Proposition — Si C est un convexe de dimension finie, les intérieurs relatifs des faces de C forment une partition de celui-ci.
Vérification des énoncés de la sectionPour la première proposition, soit c extrémal. Considérons un segment ]x,y[ dans C contenant c. Comme
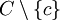 est convexe, l'une au moins de ses extrémités n'est pas dans cet ensemble, donc est égale à c. Mais un point de l'intérieur d'un segment ne peut être égal à une extrémité que si le segment est un singleton, donc x = y = c.
est convexe, l'une au moins de ses extrémités n'est pas dans cet ensemble, donc est égale à c. Mais un point de l'intérieur d'un segment ne peut être égal à une extrémité que si le segment est un singleton, donc x = y = c.Pour la deuxième proposition, soit F une face exposée et H un hyperplan d'appui avec
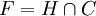 . Soit maintenant ]x,y[ un segment ouvert qui rencontre
. Soit maintenant ]x,y[ un segment ouvert qui rencontre 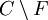 —et donc H— tout en étant tracé dans C, qui se situe d'un seul côté de H : c'est forcément que ce segment est tout entier dans H, donc aussi ses extrémités qui sont donc bien dans F.
—et donc H— tout en étant tracé dans C, qui se situe d'un seul côté de H : c'est forcément que ce segment est tout entier dans H, donc aussi ses extrémités qui sont donc bien dans F.Pour le troisième énoncé, soit F une face de dimension d − 1, H l'hyperplan affine enveloppe affine de F et c un point de l'intérieur relatif de F (c'est-à-dire de son intérieur dans H). Notons
 , si bien que
, si bien que 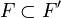 , et montrons l'inclusion réciproque ; dans cette intention prenons
, et montrons l'inclusion réciproque ; dans cette intention prenons 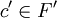 . Alors le segment [c,c'] est à extrémités dans C et, parce que c est dans l'intérieur relatif de F, le segment ouvert correspondant contient des points de F. L'extrémité finale c' de ce segment est donc aussi dans F. Vérifions ensuite que H est un hyperplan d'appui. Si ce n'était pas le cas, il existerait deux points a et b de C de part et d'autre de H (au sens strict). Le segment [a,b] serait alors un segment à extrémités hors de F dont l'intérieur, à l'endroit où il intersecte H, rencontre F' qu'on sait égal à F. Or ceci est interdit par la définition d'une face. On a finalement bien écrit F sous la forme
. Alors le segment [c,c'] est à extrémités dans C et, parce que c est dans l'intérieur relatif de F, le segment ouvert correspondant contient des points de F. L'extrémité finale c' de ce segment est donc aussi dans F. Vérifions ensuite que H est un hyperplan d'appui. Si ce n'était pas le cas, il existerait deux points a et b de C de part et d'autre de H (au sens strict). Le segment [a,b] serait alors un segment à extrémités hors de F dont l'intérieur, à l'endroit où il intersecte H, rencontre F' qu'on sait égal à F. Or ceci est interdit par la définition d'une face. On a finalement bien écrit F sous la forme 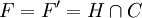 avec H hyperplan d'appui, prouvant qu'elle est exposée.
avec H hyperplan d'appui, prouvant qu'elle est exposée.Passons à la quatrième proposition. Soit ]x,y[ un segment ouvert dans C rencontrant F1. A fortiori ce segment rencontre F, qui est une face de C, donc ses extrémités sont dans F. Puisque les faces sont convexes par définition, tout le segment [x,y] est dans F. On a alors un segment dans F dont un point de l'intérieur rencontre F1 ; puisque F1 est une face de F ses deux extrémités sont dans F1.
Reste l'énoncé relatif à la partition par les intérieurs relatifs des faces. On va le montrer par récurrence sur la dimension du convexe, l'initialisation étant évidente (cas d'un point). Supposons donc le vrai pour les convexes de dimension strictement inférieure à k et soit C un convexe de dimension k.
- *La non-vacuité des intérieurs relatifs des faces provient de la condition de non-vacuité exigée des faces elles-mêmes.
- *Pour ce qui est de la réunion des intérieurs relatifs, soit c un point de C. Si c est dans l'intérieur relatif de C, en remarquant que C est lui-même une face, on a exhibé une face dont l'intérieur relatif contient c. Si c est sur la frontière, soit F une face exposée contenant c. Par l'hypothèse de récurrence, c appartient à l'intérieur relatif d'une des faces de F, qui est elle-même par l'énoncé précédent une face de C.
- *Vérifions enfin que deux intérieurs relatifs de faces sont soit égaux soit disjoints. Soit donc F1 et F2 deux faces de C dont les intérieurs relatifs se rencontrent ; notons c un point de leur intersection et G1 et G2 leurs enveloppes affines respectives. On va dans un premier temps montrer que G1 = G2 ; puisque ces sous-espaces affines passent tous deux par c, il suffit pour ce faire de s'assurer qu'ils ont même direction. Soit u un vecteur dans la direction de G1 ; comme c est dans l'intérieur relatif de F1, à condition de prendre α assez petit, les deux points c + αu et c − αu sont tous deux dans F1 donc dans C, tandis que le segment ouvert qui les joint passe par c qui est dans F2. Comme F2 est une face, les extrémités de ce segment sont aussi dans F2 et u appartient bien à la direction de G2. En échangeant les rôles de G1 et G2 on prouve l'égalité. Une fois cette étape passée, en reprenant le même argument qu'à la troisième proposition, on vérifie que
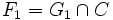 , et de même pour F2. Ceci prouve que F1 = F2 et a fortiori que les intérieurs relatifs de ces deux faces sont égaux.
, et de même pour F2. Ceci prouve que F1 = F2 et a fortiori que les intérieurs relatifs de ces deux faces sont égaux.
Contextualisation des sommets : le classement des points de la frontière selon leur ordre
En dimension finie, on vient de voir qu'à chaque point de la frontière pouvait être associée une sorte de « dimension », celle de l'unique intérieur relatif de face à laquelle il appartient.
Il y a une deuxième façon de procéder pour associer à chaque point de la frontière d'un convexe de dimension d un entier compris entre 0 et d − 1, apparentée à la définition des « sommets ».
Pour C convexe de dimension finie et c point de la frontière de C. On appelle ordre de c la dimension de l'intersection des hyperplans d'appui à C en c.
Ainsi les sommets sont les points d'ordre nul.
L'exemple très simple d'un disque du plan montre bien que cette notion ne recoupe pas la précédente : sur le cercle qui le borde, tous les points sont extrémaux, donc chaque singleton est à lui seul une face : par la division en faces, on associerait à chaque point l'entier 0. En revanche, il y a une droite d'appui unique en chaque point, et l'ordre est donc partout égal à 1.
Le cas des polyèdres convexes
Les trois notions dont cet article a fait une présentation parallèle coïncident dans le cas particulier important des polyèdres convexes (qu'on définira comme dans l'article Polytope comme étant les intersections d'un nombre fini de demi-espaces dans un espace affine de dimension finie).
Pour ce cas particulier :
Proposition — Dans un polyèdre convexe,
- toute face de la frontière est exposée ;
- l'ordre de chaque point de la frontière est égal à la dimension de l'unique intérieur relatif de face auquel il appartient.
En particulier il y a identité de l'ensemble des sommets et de celui des points extrémaux. Pour un polyèdre convexe compact, le théorème de Minkowski peut donc aussi être énoncé comme assurant qu'il est enveloppe convexe de l'ensemble de ses sommets.
Quelques autres informations relatives à la division en faces d'un polyèdre convexe, qu'on démontre concurremment à la proposition précédente, méritent d'être signalées dans ce rapide survol. Rappelons qu'on appelle facettes d'un convexe de dimension d ses faces de dimension d − 1 :
Proposition — Dans un polyèdre convexe C,
- les facettes sont en nombre fini et couvrent toute la frontière relative, ce sont elles-mêmes des polyèdres convexes ;
- toute face propre de C est elle-même face d'une facette de C.
Une conséquence est qu'on obtient toutes les faces propres en considérant les facettes, puis les facettes des facettes, etc... Les faces sont donc en nombre fini, et en particulier les sommets : tout polyèdre convexe compact est donc l'enveloppe convexe d'un nombre fini de points.
Références
Sauf précisions contraires, les informations fournies dans cet article sont issues de Fundamentals of convex analysis, de Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, coll. « Grundlehren Text Editions », Springer, 2001 (ISBN 3540422056) p. 41-45, 57 ou 246.
Marcel Berger, Géométrie [détail des éditions] a servi de source pour les sections consacrées aux sommets (section 11.6, tome 3, p. 50-52 dans l'édition de 1978), à l'ordre en un point (même section, p. 50) et au cas des polyèdres convexes (section 12.1, p. 89-90).
Catégorie : Géométrie convexe
Wikimedia Foundation. 2010.