- Espace Localement Convexe
-
Espace localement convexe
Sommaire
Définition
Un espace vectoriel topologique E est dit localement convexe s'il vérifie l'une des deux propriétés équivalentes suivantes :
- (i) La topologie de E peut être définie par une famille filtrante de semi-normes
- (ii) 0 possède une base de voisinages formée de convexes
Démonstration de l'équivalence des 2 définitions
(i) (ii)
(ii)
En effet toute semi-norme sur E est une fonction convexe et donc pour tout R>0 l'ensemble des x de E vérifiant p(x)<R est convexe.
(ii) (i)
(i)- Supposons d'abord que E est un espace réel.
Si V est un voisinage convexe de 0 alors
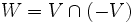 est un voisinage convexe et symétrique de 0. Il est absorbant. Il en résulte que la jauge de W est une semi-norme sur E et ces semi-normes définissent la topologie de E.
est un voisinage convexe et symétrique de 0. Il est absorbant. Il en résulte que la jauge de W est une semi-norme sur E et ces semi-normes définissent la topologie de E.- Supposons maintenant que E est un espace complexe.
Nous allons montrer que tout voisinage convexe de l'origine contient un voisinage convexe équilibré.
Soit en effet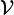 un voisinage convexe de 0. Par application de la continuité de l'application de
un voisinage convexe de 0. Par application de la continuité de l'application de  dans
dans 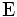 :
:  , il existe α > 0 et un voisinage
, il existe α > 0 et un voisinage 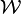 de 0 tels que | λ | < α et
de 0 tels que | λ | < α et 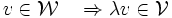 .
.
Soit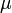 un scalaire vérifiant | μ | < α. Alors
un scalaire vérifiant | μ | < α. Alors 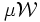 est un voisinage de 0 inclus dans
est un voisinage de 0 inclus dans 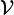 . Si
. Si 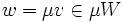 et
et 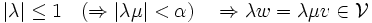 . Ceci entraîne que x appartient au noyau équilibré de
. Ceci entraîne que x appartient au noyau équilibré de 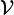 .
.
Ce noyau équilibré (contenant ) est un voisinage de 0. Son enveloppe convexe est un voisinage convexe et équilibré de 0 inclus dans
) est un voisinage de 0. Son enveloppe convexe est un voisinage convexe et équilibré de 0 inclus dans 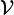 (puisque
(puisque 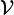 est convexe).
est convexe).
La jauge de ce noyau équilibré est une semi-norme sur E (ce noyau est un voisinage de 0 donc absorbant ). Ces semi-normes définissent la topologie de E.Critère de séparation
Théorème
- Pour qu'un espace localement convexe E défini par la famille
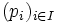 soit un espace séparé, il faut et il suffit que pour tout
soit un espace séparé, il faut et il suffit que pour tout 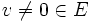 il existe une semi-norme
il existe une semi-norme  telle que
telle que 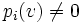 .
.
Continuité d'une fonction
Soient
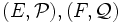 2 espaces localement convexes,
2 espaces localement convexes, 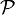 et
et 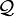 étant des familles de semi-normes définissant les topologies et f une application du premier espace dans le second. Alors il résulte de la définition même que f est continue en
étant des familles de semi-normes définissant les topologies et f une application du premier espace dans le second. Alors il résulte de la définition même que f est continue en  si et seulement si
si et seulement si
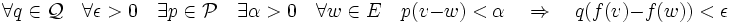
On peut aussi définir la continuité uniforme. f est uniformément continue si

Espace métrisable
- Un espace localement convexe est métrisable ssi il est séparé et sa topologie peut être définie par une famille dénombrable de semi-normes.
Le qualificatif "métrisable" est justifié par le théorème suivant:
Théorème- Si E est un espace localement convexe métrisable, il existe une distance invariante par translation définissant la même topologie que celle de E.
Démonstration:
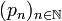 désignant une famille filtrante de semi-normes définissant la topologie de E, posons pour tout
désignant une famille filtrante de semi-normes définissant la topologie de E, posons pour tout 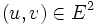
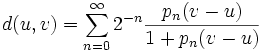 .
.
Remarque: En fait la structure d'espace localement convexe est souvent définie par une famille quelconque de semi-normes (cf. semi-norme). Cependant on peut, comme vu dans cet article, la compléter pour obtenir une famille filtrante. Cette complétion est toujours sous-entendue dans les démonstrations. De plus, la procédure indiquée (rajouter les sup des sous-familles finies) conserve ici le caractère dénombrable de cette famille complétée (Le cardinal de cette famille complétée est majoré par celui des parties finies de la suite initiale, qu'on peut mettre en bijection avec les entiers écrits en binaire).- Tout d'abord, on voit aisément que d(u,v) est bien défini pour tous u, v (série positive convergente).
- Ensuite il est aisé de démontrer qu'il s'agit bien d'une distance sur E (en particulier le critère de séparation ci-dessus montre que
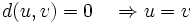 ).
). - L'invariance par translation de cette distance est également immédiate (
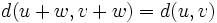 ).
). - Il reste enfin à montrer que la topologie définie par cette distance est identique à celle définie par la famille de semi-normes. Comme la distance est invariante par translation, il suffit de montrer que toute boule (ouverte) de centre 0 pour la distance d contient une "p-boule" de centre 0 et réciproquement. Autrement dit:
- (i)
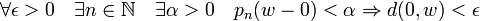
- (ii)

-
- Démontrons (i). Soit ε > 0
- Démontrons (i). Soit ε > 0
Le terme général de la série définissant
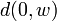 etant majoré par
etant majoré par 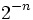 , on peut tout d'abord trouver
, on peut tout d'abord trouver  tel que
tel que 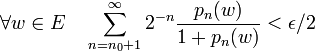 .
.
Ensuite, la famille de semi-normes étant filtrante, on peut trouver une semi-norme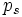 majorant toutes les semi-normes
majorant toutes les semi-normes 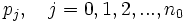 .
.
Comme l'application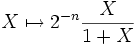 de
de 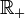 sur
sur ![\quad [0,2^{-n}]](/pictures/frwiki/98/bc4f4668741d0cdb3924eb0f5ec0904f.png) est croissante, on en déduit que
est croissante, on en déduit que 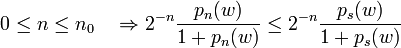 .
.
On obtient alors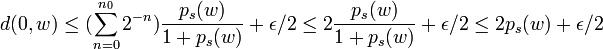
Il suffit alors de poser α = ε / 4. CQFD-
- Démontrons maintenant(ii). Soit encore ε > 0
D'après la définition de d(u,v), on doit avoir:
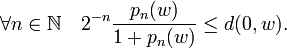
On définit l'homographie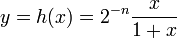 . On a donc
. On a donc  .
.
L'homographie inverse est donnée par . .Cette homographie inverse est continue en 0 et est strictement croissante.
. .Cette homographie inverse est continue en 0 et est strictement croissante.
On a donc . On veut choisir α tel que si
. On veut choisir α tel que si 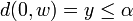 , alors
, alors 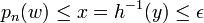 . Il suffit donc de choisir α tel que h − 1(α) = ε.
. Il suffit donc de choisir α tel que h − 1(α) = ε.
Donc on choisit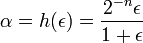 . CQFD
. CQFDEspace de Fréchet
- Un espace de Fréchet est un espace localement convexe métrisable et complet
Remarquons qu'un espace de Banach est un espace de Fréchet (topologie définie par une seule semi-norme: la norme). Cependant la réciproque n'est pas vraie car si d est la distance définie ci-dessus, d(0,v) n'est en général pas une norme sur E.
- Tout espace de Fréchet est un espace de Baire.
En effet la topologie est celle d'un espace métrique complet (voir théorème de Baire)
- Portail des mathématiques
Catégories : Géométrie convexe | Espace vectoriel topologique
Wikimedia Foundation. 2010.
