Inegalite arithmetico-geometrique
- Inegalite arithmetico-geometrique
-
Inégalité arithmético-géométrique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inegalite arithmetico-geometrique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inégalité arithmético-géométrique — En mathématiques, l inégalité arithmético géométrique établit un lien entre la moyenne arithmétique et la moyenne géométrique. C est un résultat classique lié à la convexité. Énoncé Étant donnés n réels strictement positifs , on définit leur… … Wikipédia en Français
Inegalite de Jensen — Inégalité de Jensen En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de … Wikipédia en Français
Inégalité De Jensen — En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de deux manières … Wikipédia en Français
Inégalité de jensen — En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de deux manières … Wikipédia en Français
Inegalite de Holder — Inégalité de Hölder En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans… … Wikipédia en Français
Inégalité De Hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français
Inégalité de hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français
Inégalité de Jensen — En mathématiques, et plus précisément en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de … Wikipédia en Français
Inégalité (mathématiques) — Pour les articles homonymes, voir inégalité. En mathématiques, une inégalité est un énoncé permettant de comparer la taille, ou l ordre de deux objets (dans le cas où ils seraient égaux, on a une égalité) La notation a < b signifie que a est… … Wikipédia en Français
Inégalité de Hölder — En analyse, l’inégalité de Hölder, ainsi nommée en l honneur de Otto Hölder, est une inégalité fondamentale relative aux espaces de fonctions Lp et aux espaces de suites . Sommaire 1 Enoncé 2 Applications … Wikipédia en Français
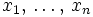 , on définit leur moyenne arithmétique
, on définit leur moyenne arithmétique 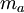 et leur moyenne géométrique
et leur moyenne géométrique 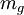 :
: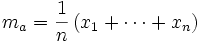 et
et ![m_g = \sqrt[n\,]{x_1 \cdots x_n}](/pictures/frwiki/50/2afa3a71dcdd6defdfc6fa74e4444f36.png) .
.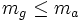 .
.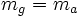 si et seulement si les
si et seulement si les 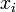 sont tous égaux.
sont tous égaux.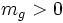 et
et 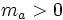 ,
, 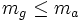 équivaut (par croissance stricte du logarithme)
équivaut (par croissance stricte du logarithme)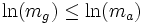 ,
,![\frac{1}{n}\, \left[\,\ln(x_1) + \cdots + \ln(x_n)\right] \leq \ln \left(\frac{x_1 + \cdots + x_n}{n}\right)](/pictures/frwiki/102/f75cc1c6f70ca31be1f0bbb6ff7a40b6.png) .
.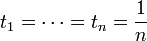 .
.