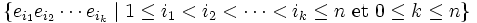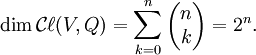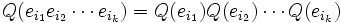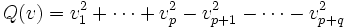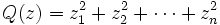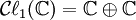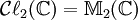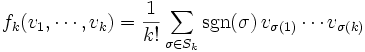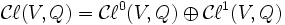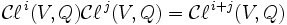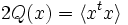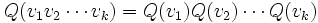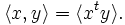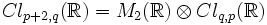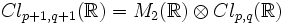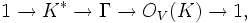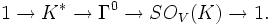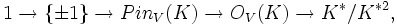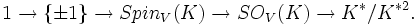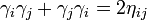- Algebre de Clifford
-
Algèbre de Clifford
En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l'une des généralisations possibles des nombres complexes et des quaternions. Elles ont été nommées en l'honneur du mathématicien anglais William Kingdon Clifford.
- Une certaine familiarité avec les bases de l'algèbre multilinéaire sera très utile à la lecture de cet article.
Introduction et propriétés de base
Précisément, une algèbre de Clifford est une algèbre associative unitaire qui est engendrée par un espace vectoriel V muni d'une forme quadratique Q.
L'algèbre de Clifford
 est l'algèbre « la plus générale » engendrée par V soumise à la condition1
est l'algèbre « la plus générale » engendrée par V soumise à la condition1où le produit v2 est pris à l'intérieur de l'algèbre et le réel Q(v) est identifié à Q(v)·1, 1 désignant l'unité de l'algèbre. Si la caractéristique du corps de base K n'est pas 2, alors on peut ré-écrire cette identité fondamentale sous la forme
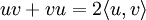 pour tout
pour tout 
où
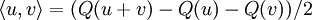 est la forme bilinéaire symétrique associée à Q.
est la forme bilinéaire symétrique associée à Q.Cette idée d'algèbre « la plus générale » soumise à cette identité peut être formellement exprimée à travers la notion de propriété universelle (voir ci-dessous).
Les algèbres de Clifford sont directement reliées aux algèbres extérieures. En fait, si Q = 0 alors l'algèbre de Clifford
 est simplement l'algèbre extérieure
est simplement l'algèbre extérieure 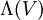 . Pour Q différent de zéro, il existe un isomorphisme canonique linéaire entre
. Pour Q différent de zéro, il existe un isomorphisme canonique linéaire entre 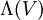 et
et  toutes les fois que le corps de base K n'est pas de caractéristique 2. C’est-à-dire qu'ils sont naturellement isomorphes comme espaces vectoriels mais avec des multiplications différentes. La multiplication de Clifford est plus riche que le produit extérieur puisqu'il fait usage d'une information supplémentaire fournie par Q.
toutes les fois que le corps de base K n'est pas de caractéristique 2. C’est-à-dire qu'ils sont naturellement isomorphes comme espaces vectoriels mais avec des multiplications différentes. La multiplication de Clifford est plus riche que le produit extérieur puisqu'il fait usage d'une information supplémentaire fournie par Q.Les formes quadratiques et les algèbres de Clifford de caractéristique 2 forment un cas exceptionnel. En particulier, si la caractéristique de K = 2, il n'est pas vrai qu'une forme quadratique est déterminée par sa forme bilinéaire symétrique, ou que chaque forme quadratique admet une base orthogonale. Beaucoup de résultats dans cet article incluent la condition que la caractéristique n'est pas 2, et sont faux si cette condition est enlevée.
Construction et propriété universelle
Soit V un espace vectoriel sur un corps K, et
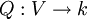 une forme quadratique sur V. Une algèbre de Clifford
une forme quadratique sur V. Une algèbre de Clifford 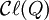 est une algèbre associative unitaire sur K munie d'une application linéaire
est une algèbre associative unitaire sur K munie d'une application linéaire 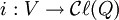 définie par la propriété universelle suivante :
définie par la propriété universelle suivante :Pour toute algèbre associative A sur K munie d'une application linéaire
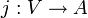 vérifiant j(v)2 = Q(v)1 pour chaque vecteur v de V (où 1 désigne le neutre multiplicatif de A), il existe un unique homomorphisme d'algèbres
vérifiant j(v)2 = Q(v)1 pour chaque vecteur v de V (où 1 désigne le neutre multiplicatif de A), il existe un unique homomorphisme d'algèbres 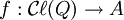 faisant commuter le diagramme suivant :
faisant commuter le diagramme suivant :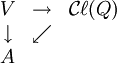
c'est-à-dire que
 .
.En travaillant avec la forme bilinéaire symétrique
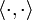 associée à Q (de caractéristique différente de 2), la condition sur j est
associée à Q (de caractéristique différente de 2), la condition sur j est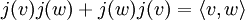 pour tout v w ∈ V.
pour tout v w ∈ V.
Une algèbre de Clifford comme décrite ci-dessus existe toujours et peut être construite comme suit : Démarrer avec l'algèbre la plus générale qui contient V, concrètement l'algèbre tensorielle T(V), puis imposer l'identité fondamentale en prenant un quotient convenable. Dans notre cas, nous voulons prendre l'idéal bilatère
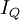 dans
dans 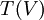 engendré par tous les éléments de la forme
engendré par tous les éléments de la forme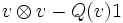 pour tout
pour tout 
et définissons
 comme le quotient
comme le quotient .
.
Il est alors plus direct de montrer que
 contient V et satisfait la propriété universelle ci-dessus, donc que
contient V et satisfait la propriété universelle ci-dessus, donc que 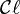 est unique à un isomorphisme près; ainsi on parle de l'algèbre de Clifford
est unique à un isomorphisme près; ainsi on parle de l'algèbre de Clifford  . Il suit aussi de cette construction que i est injective. Habituellement, on laisse tomber le i et on considère V comme un sous-espace vectoriel de
. Il suit aussi de cette construction que i est injective. Habituellement, on laisse tomber le i et on considère V comme un sous-espace vectoriel de  .
.Une conséquence de la définition est que pour tous vecteurs u,v de V, l'identité
 est vraie dans C(Q). Si le corps n'est pas de caractéristique 2, cette propriété peut être utilisée en tant que définition alternative.
est vraie dans C(Q). Si le corps n'est pas de caractéristique 2, cette propriété peut être utilisée en tant que définition alternative.La caractérisation universelle des algèbres de Clifford montre que la construction de
 est de nature fonctorielle. Concrètement,
est de nature fonctorielle. Concrètement, 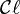 peut être considéré comme un foncteur issu de la catégorie des espaces vectoriels avec formes quadratiques (dont les morphismes sont des applications linéaires préservant la forme quadratique) vers la catégorie des algèbres associatives. La propriété universelle garantit que les applications linéaires entre les espaces vectoriels (préservant la forme quadratique) s'étendent de façon unique vers les homomorphismes d'algèbre entre les algèbres de Clifford associées.
peut être considéré comme un foncteur issu de la catégorie des espaces vectoriels avec formes quadratiques (dont les morphismes sont des applications linéaires préservant la forme quadratique) vers la catégorie des algèbres associatives. La propriété universelle garantit que les applications linéaires entre les espaces vectoriels (préservant la forme quadratique) s'étendent de façon unique vers les homomorphismes d'algèbre entre les algèbres de Clifford associées.Base et dimension
Si la dimension de V est n et
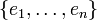 est une base de V, alors l'ensemble
est une base de V, alors l'ensembleest une base de
 . Le produit vide (k = 0) est défini comme l'élément neutre multiplicatif. Pour chaque valeur de k, il existe
. Le produit vide (k = 0) est défini comme l'élément neutre multiplicatif. Pour chaque valeur de k, il existe  éléments de la base, donc, la dimension totale de l'algèbre de Clifford est
éléments de la base, donc, la dimension totale de l'algèbre de Clifford estSi la caractéristique n'est pas 2, il existe un ensemble de bases privilégiées pour V : les bases orthogonales. Une base orthogonale est telle que
où <·,·> est la forme bilinéaire symétrique associée à Q. L'identité de Clifford fondamentale implique que pour une base orthogonale
Ceci rend la manipulation des vecteurs de la base orthogonale tout à fait simple. Etant donné un produit
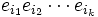 de vecteurs distincts de la base orthogonale, on peut les placer dans un ordre standard en incluant un signe correspondant au nombre de permutations nécessaires pour les ordonner correctement (i.e. la signature de la permutation ordonnée).
de vecteurs distincts de la base orthogonale, on peut les placer dans un ordre standard en incluant un signe correspondant au nombre de permutations nécessaires pour les ordonner correctement (i.e. la signature de la permutation ordonnée).On peut aisément étendre la forme quadratique sur V vers une forme quadratique sur
 en demandant que les éléments distincts
en demandant que les éléments distincts 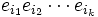 soient orthogonaux entre eux, et en posant :
soient orthogonaux entre eux, et en posant :En particulier Q(1) = 1 et la forme quadratique sur un scalaire est simplement
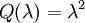 . Ainsi, les bases orthogonales de V peuvent être étendues en une base orthogonale de
. Ainsi, les bases orthogonales de V peuvent être étendues en une base orthogonale de  . La forme quadratique définie de cette manière est en fait indépendante de la base orthogonale choisie (une formulation indépendante de la base sera donnée plus bas).
. La forme quadratique définie de cette manière est en fait indépendante de la base orthogonale choisie (une formulation indépendante de la base sera donnée plus bas).Exemples : les algèbres de Clifford réelles et complexes
Les algèbres de Clifford les plus importantes sont celles sur les espaces vectoriels réels et complexes muni de formes quadratiques non dégénérées.
Chaque forme quadratique non dégénérée sur un espace vectoriel réel de dimension finie est équivalente à la forme diagonale standard :
où n = p + q est la dimension de l'espace vectoriel. La paire d'entiers (p, q) est appelée la signature de la forme quadratique. L'espace vectoriel avec cette forme quadratique est souvent noté
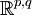 . L'algèbre de Clifford sur
. L'algèbre de Clifford sur 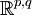 est notée
est notée 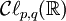 . Le symbole
. Le symbole 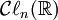 signifie soit
signifie soit 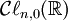 ou
ou 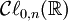 selon que les auteurs préfèrent des espaces définis positifs ou négatifs.
selon que les auteurs préfèrent des espaces définis positifs ou négatifs.Une base orthonormale standard {ei} pour
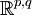 consiste en n = p + q vecteur mutuellement orthogonaux, p ont une norme +1 et q ont une norme -1. L'algèbre
consiste en n = p + q vecteur mutuellement orthogonaux, p ont une norme +1 et q ont une norme -1. L'algèbre 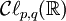 aura par conséquent p vecteurs dont le carré sera égal à +1 et q vecteurs dont le carré sera égal à -1.
aura par conséquent p vecteurs dont le carré sera égal à +1 et q vecteurs dont le carré sera égal à -1. est naturellement isomorphe à
est naturellement isomorphe à 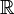 puisqu'il n'y a pas de vecteurs différents de zéro.
puisqu'il n'y a pas de vecteurs différents de zéro.
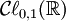 est une algèbre à deux dimensions engendrée par un vecteur unique e1 dont le carré est égal à -1, et par conséquent est isomorphe à
est une algèbre à deux dimensions engendrée par un vecteur unique e1 dont le carré est égal à -1, et par conséquent est isomorphe à 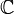 , le corps des nombres complexes.
, le corps des nombres complexes.
- L'algèbre
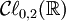 est une algèbre à quatre dimensions engendrée par {1, e1, e2, e1e2}. Les trois derniers éléments ont le carré égal à -1 et anticommutent tous, et donc, l'algèbre est isomorphe aux quaternions
est une algèbre à quatre dimensions engendrée par {1, e1, e2, e1e2}. Les trois derniers éléments ont le carré égal à -1 et anticommutent tous, et donc, l'algèbre est isomorphe aux quaternions 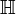 .
.
- L'algèbre suivante dans la suite,
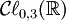 , est une algèbre à huit dimensions isomorphe à la somme directe
, est une algèbre à huit dimensions isomorphe à la somme directe 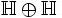 appelée les biquaternions de Clifford.
appelée les biquaternions de Clifford.
On peut aussi étudier les algèbres de Clifford sur les espaces vectoriels complexes. Chaque forme quadratique non dégénérée sur un espace vectoriel complexe est équivalent à la forme diagonale standard
où n = dim V, donc il existe essentiellement une seule algèbre de Clifford dans chaque dimension. Nous noterons l'algèbre de Clifford sur
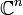 avec la forme quadratique standard par
avec la forme quadratique standard par 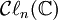 . On peut montrer que l'algèbre
. On peut montrer que l'algèbre 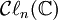 peut être obtenue par la complexification de l'algèbre
peut être obtenue par la complexification de l'algèbre 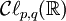 où n = p + q:
où n = p + q: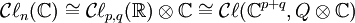 .
.
Ici Q est la forme quadratique réelle de signature (p,q).
Note : la complexification ne dépend de la signature. Les premiers cas ne sont pas difficiles à calculer. On trouve que
où
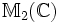 représente l'algèbre de matrices 2 x 2 sur
représente l'algèbre de matrices 2 x 2 sur 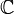 .
.Il s'avère que chacune des algèbres
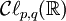 et
et 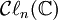 est isomorphe à l'algèbre de matrices sur
est isomorphe à l'algèbre de matrices sur 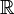 ,
, 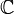 ou
ou 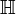 ou à la somme directe de deux algèbres de cette sorte. Pour une classification complète de ces algèbres :Article détaillé : classification des algèbres de Clifford.
ou à la somme directe de deux algèbres de cette sorte. Pour une classification complète de ces algèbres :Article détaillé : classification des algèbres de Clifford.Propriétés
Relation avec l'algèbre extérieure
Etant donné un espace vectoriel V, on peut construire l'algèbre extérieure
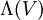 , dont la définition est indépendante de toute forme quadratique sur V. Il s'avère que si F n'est pas de caractéristique 2 alors il existe un isomorphisme naturel entre
, dont la définition est indépendante de toute forme quadratique sur V. Il s'avère que si F n'est pas de caractéristique 2 alors il existe un isomorphisme naturel entre 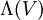 et
et  considéré comme des espaces vectoriels. C'est un isomorphisme d'algèbre si et seulement si Q = 0. On peut ainsi considérer l'algèbre de Clifford
considéré comme des espaces vectoriels. C'est un isomorphisme d'algèbre si et seulement si Q = 0. On peut ainsi considérer l'algèbre de Clifford  comme un enrichissement de l'algèbre extérieure sur V avec une multiplication qui dépend de Q.
comme un enrichissement de l'algèbre extérieure sur V avec une multiplication qui dépend de Q.La manière la plus facile d'établir l'isomorphisme est de choisir une base orthogonale {ei} pour V et de l'étendre en une base orthogonale pour
 comme décrit ci-dessus. L'application
comme décrit ci-dessus. L'application 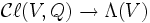 est déterminée par
est déterminée par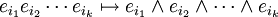 .
.
Note : Ceci fonctionne seulement si la base {ei} est orthogonale. On peut montrer que cette application est indépendante du choix de la base orthogonale et donc donne un isomorphisme naturel.
Si la caractéristique de K est 0, on peut aussi établir l'isomorphisme par antisymétrie. Définissons les fonctions
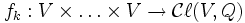 par
paroù la somme est prise sur le groupe symétrique sur k éléments, et où sgn(σ) est la signature de la permutation σ. fk est alternée, et induit une application linéaire unique
 . La somme directe de ces applications donne une application linéaire entre
. La somme directe de ces applications donne une application linéaire entre 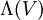 et
et  . On peut montrer que cette application est un isomorphisme linéaire.
. On peut montrer que cette application est un isomorphisme linéaire.Une autre manière de voir la relation est la construction d'un filtre sur
 . Rappelons que l'algèbre tensorielle T(V) possède un filtre naturel :
. Rappelons que l'algèbre tensorielle T(V) possède un filtre naturel : 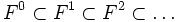 où Fk contient les sommes de tenseurs de rang ≤ k. Projeter ceci vers l'algèbre de Clifford donne un filtre sur
où Fk contient les sommes de tenseurs de rang ≤ k. Projeter ceci vers l'algèbre de Clifford donne un filtre sur  . L'algèbre graduée associée
. L'algèbre graduée associéeest naturellement isomorphe à l'algèbre extérieure
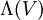 .
.Une manière plus simple est de voir qu'en choisissant une base
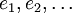 de V, on peut toujours exprimer, grâce à la relation d'anticommutativité, un élément de l'algèbre de Clifford comme combinaison linéaire de monômes du type :
de V, on peut toujours exprimer, grâce à la relation d'anticommutativité, un élément de l'algèbre de Clifford comme combinaison linéaire de monômes du type : ,
,
ce qui donne un isomorphisme explicite avec l'algèbre extérieure. Notons que ce n'est qu'un isomorphisme d'espaces vectoriels.
Si V est de dimension finie paire, que le corps est algébriquement clos et que la forme quadratique est non dégénérée, l'algèbre de Clifford est centrale simple. Ainsi, par le théorème d'Artin-Wedderburn, elle est (non canoniquement) isomorphe à une algèbre de matrices. Il s'ensuit que dans ce cas, C(q) possède une représentation irréductible de dimension
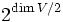 , qui est unique à un isomorphisme (non unique) près. C'est la (sulfureusement) célèbre représentation spinorielle, dont les vecteurs sont appelés spineurs.
, qui est unique à un isomorphisme (non unique) près. C'est la (sulfureusement) célèbre représentation spinorielle, dont les vecteurs sont appelés spineurs.Graduation
L'application linéaire sur V définie par
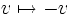 conserve la forme quadratique Q et donc, par la propriété universelle des algèbres de Clifford s'étend à un automorphisme d'algèbre
conserve la forme quadratique Q et donc, par la propriété universelle des algèbres de Clifford s'étend à un automorphisme d'algèbre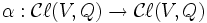 .
.
Puisque
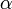 est une involution (i.e. son carré est l'identité), on peut décomposer
est une involution (i.e. son carré est l'identité), on peut décomposer  en deux espaces propres positifs et négatifs
en deux espaces propres positifs et négatifsoù
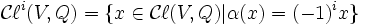 . Puisque
. Puisque 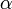 est un automorphisme, il vient
est un automorphisme, il vientoù les indices supérieurs sont lus modulo 2. Ceci signifie que
 est une
est une 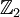 -algèbre graduée (aussi connue comme une superalgèbre).
-algèbre graduée (aussi connue comme une superalgèbre).Note :
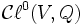 forme une sous-algèbre de
forme une sous-algèbre de  , appelée la sous-algèbre paire. La partie
, appelée la sous-algèbre paire. La partie 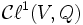 est appelée la partie impaire de
est appelée la partie impaire de  (ce n'est pas une sous-algèbre). Cette
(ce n'est pas une sous-algèbre). Cette 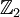 -graduation joue un rôle important dans l'analyse et l'application des algèbres de Clifford. L'automorphisme
-graduation joue un rôle important dans l'analyse et l'application des algèbres de Clifford. L'automorphisme 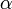 est appelé l'involution principale ou l'involution de grade.
est appelé l'involution principale ou l'involution de grade.Remarque. En caractéristique différente de 2, l'algèbre
 hérite d'une
hérite d'une 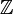 -graduation de l'isomorphisme canonique avec l'algèbre extérieure
-graduation de l'isomorphisme canonique avec l'algèbre extérieure 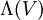 . Néanmoins, ceci est un espace vectoriel seulement gradué, c’est-à-dire que la multiplication de Clifford ne respecte pas la
. Néanmoins, ceci est un espace vectoriel seulement gradué, c’est-à-dire que la multiplication de Clifford ne respecte pas la 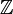 -graduation, seulement la
-graduation, seulement la 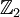 -graduation. Heureusement, les graduations sont reliées d'une manière naturelle :
-graduation. Heureusement, les graduations sont reliées d'une manière naturelle : 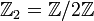 . Le degré d'un nombre de Clifford fait référence généralement au degré dans la
. Le degré d'un nombre de Clifford fait référence généralement au degré dans la 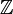 -graduation. Les éléments qui sont homogènes dans la
-graduation. Les éléments qui sont homogènes dans la 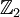 -graduation sont simplement dits pairs ou impairs.
-graduation sont simplement dits pairs ou impairs.Si la caractéristique de K n'est pas 2, alors la sous-algèbre paire
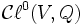 d'une algèbre de Clifford est elle-même une algèbre de Clifford. Si V est la somme directe orthogonale d'un vecteur a de norme Q(a) et un sous-espace U, alors
d'une algèbre de Clifford est elle-même une algèbre de Clifford. Si V est la somme directe orthogonale d'un vecteur a de norme Q(a) et un sous-espace U, alors 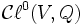 est isomorphe à
est isomorphe à 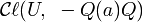 , où -Q(a)Q est la forme Q restreinte à U et multipliée par -Q(a). En particulier sur les réels, ceci implique que
, où -Q(a)Q est la forme Q restreinte à U et multipliée par -Q(a). En particulier sur les réels, ceci implique que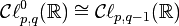 pour q > 0 et
pour q > 0 et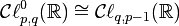 pour p > 0.
pour p > 0.
Dans le cas défini négatif, cela donne une inclusion
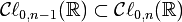 qui étend la suite
qui étend la suiteDe même, dans le cas complexe, on peut montrer que la sous-algèbre paire de
 est isomorphe à
est isomorphe à 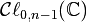 .
.L'algèbre de Clifford
 est filtrée par les sous-espaces
est filtrée par les sous-espaces 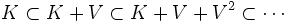 constitués d'éléments pouvant être écrits comme monômes en 0, 1, 2 ... vecteurs de V. L'algèbre graduée associée est canoniquement isomorphe à l'algèbre extérieure
constitués d'éléments pouvant être écrits comme monômes en 0, 1, 2 ... vecteurs de V. L'algèbre graduée associée est canoniquement isomorphe à l'algèbre extérieure 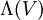 de l'espace vectoriel. Cela montre en particulier que
de l'espace vectoriel. Cela montre en particulier que 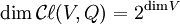 .
.Anti-automorphismes
En plus de l'automorphisme
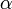 , il existe deux anti-automorphismes qui jouent un rôle important dans l'analyse des algèbres de Clifford. Rappelons que l'algèbre tensorielle T(V) possède un anti-automorphisme qui renverse l'ordre de tous les produits :
, il existe deux anti-automorphismes qui jouent un rôle important dans l'analyse des algèbres de Clifford. Rappelons que l'algèbre tensorielle T(V) possède un anti-automorphisme qui renverse l'ordre de tous les produits :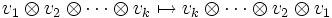 .
.
Puisque l'idéal
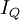 est invariant sous ce renversement, cette opération descend vers un anti-automorphisme de
est invariant sous ce renversement, cette opération descend vers un anti-automorphisme de 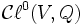 appelé l'opération de transposition ou de renversement, notée par
appelé l'opération de transposition ou de renversement, notée par  . La transposition est un anti-automorphisme :
. La transposition est un anti-automorphisme : 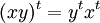 . L'opération de transposition ne fait pas usage de la
. L'opération de transposition ne fait pas usage de la 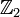 -graduation donc nous définissons un deuxième anti-automorphisme par composition d'α et la transposition. Nous appelons cette opération la conjugaison de Clifford notée
-graduation donc nous définissons un deuxième anti-automorphisme par composition d'α et la transposition. Nous appelons cette opération la conjugaison de Clifford notée 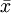
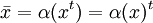 .
.
De ces deux anti-automorphismes, la transposition est la plus fondamentale.3
Note : Toutes ces opérations sont des involutions. On peut montrer qu'ils agissent comme ±1 sur les éléments qui sont homogènes dans la
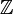 -graduation. En fait, toutes les trois opérations dépendent seulement sur le degré modulo 4. C’est-à-dire, si x est homogène avec un degré k, alors
-graduation. En fait, toutes les trois opérations dépendent seulement sur le degré modulo 4. C’est-à-dire, si x est homogène avec un degré k, alors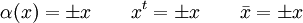 où les signes sont donnés par la table suivante :
où les signes sont donnés par la table suivante :
k mod 4 0 1 2 3 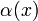
+ - + - 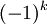

+ + - - 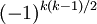
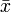
+ - - + 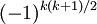
Le produit scalaire de Clifford
Lorsque la caractéristique n'est pas 2, la forme quadratique Q sur V peut être étendue à une forme quadratique sur toutes les
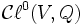 comme expliqué plus haut (et que nous avons aussi notée par Q). Une définition de base indépendante est
comme expliqué plus haut (et que nous avons aussi notée par Q). Une définition de base indépendante estoù <a> désigne la partie scalaire de a (la partie de graduation 0 dans la
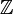 -graduation). On peut montrer que
-graduation). On peut montrer queoù les vi sont les éléments de V — cette identité n'est pas vraie pour des éléments arbitraires de
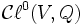 .
.La forme bilinéaire symétrique associée sur
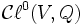 est donnée par
est donnée parOn peut vérifier que ceci se réduit à la forme bilinéaire originale lorsqu'elle est restreinte à V. La forme bilinéaire de toutes les
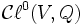 est non dégénérée si et seulement si elle n'est pas dégénérée sur V.
est non dégénérée si et seulement si elle n'est pas dégénérée sur V.Il n'est pas difficile de vérifier que la transposition est l'adjoint de la multiplication de Clifford gauche/droite avec le respect de ce produit intérieur. C’est-à-dire,
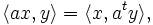 et
et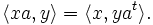
Structure des algèbres de Clifford
Dans cette partie, nous supposons que l'espace vectoriel V est de dimension finie et que la forme bilinéaire de Q est non-dégénérée. Une algèbre centrale simple sur K est une algèbre de matrices sur une algèbre de division (de dimension finie) avec un centre K. Par exemple, les algèbres centrales simples sur les réels sont les algèbres de matrices sur soit les réels, soit les quaternions.
- Si V possède une dimension paire, alors
 est une algèbre centrale simple sur K.
est une algèbre centrale simple sur K. - Si V possède une dimension paire, alors
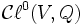 est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes.
est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes. - Si V possède une dimension impaire, alors
 est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes.
est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes. - Si V possède une dimension impaire, alors
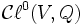 est une algèbre centrale simple sur K.
est une algèbre centrale simple sur K.
La structure des algèbres de Clifford peut être établie explicitement en utilisant le résultat suivant. Supposons que U possède une dimension paire et une forme bilinéaire non-singulière avec un discriminant d, et supposons que V est un autre espace vectoriel avec une forme quadratique. L'algèbre de Clifford de U+V est isomorphe au produit tensoriel des algèbres de Clifford de U et
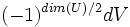 , qui est l'espace V avec sa forme quadratique multiplié par
, qui est l'espace V avec sa forme quadratique multiplié par 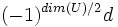 . Sur les réels, cela implique en particulier que
. Sur les réels, cela implique en particulier queCes formules peuvent être utilisées pour trouver la structure de toutes les algèbres de Clifford réelles;
Article détaillé : classification des algèbres de Clifford.Le groupe Γ de Clifford
Dans cette partie, nous supposons que V est de dimension finie et que la forme bilinéaire de Q est non-singulière.
Le groupe de Clifford
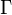 est défini comme étant l'ensemble des éléments inversibles x de l'algèbre de Clifford tels que
est défini comme étant l'ensemble des éléments inversibles x de l'algèbre de Clifford tels quepour tout v dans V. Cette formule définit aussi une action du groupe de Clifford sur l'espace vectoriel V qui conserve la norme Q et donc, donne un homomorphisme du groupe de Clifford vers le groupe orthogonal. Le groupe de Clifford contient tout les éléments r de V de norme différente de zéro, et ceux-ci agissent sur V par les réflexions correspondantes que prennent v vers v − <v,r>r/Q(r) (En caractéristique 2, ceux-ci sont appelée des transvections orthogonales plutôt que réflexions).
Beaucoup d'auteurs définissent le groupe de Clifford légèrement différemment, en remplaçant l'action
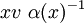 par
par 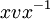 . Ceci produit le même groupe de Clifford, mais l'action du groupe de Clifford sur V est changée légèrement : l'action des éléments impairs
. Ceci produit le même groupe de Clifford, mais l'action du groupe de Clifford sur V est changée légèrement : l'action des éléments impairs 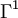 du groupe de Clifford est multiplié par un facteur extérieur à -1.
du groupe de Clifford est multiplié par un facteur extérieur à -1.L'action utilisée ici possède plusieurs petits avantages : elle est conforme avec les conventions usuelles de signes de superalgèbre, les éléments de V correspondent aux reflexions et dans les dimensions impaires, l'application du groupe de Clifford vers le groupe orthogonal est sur, et le noyau n'est pas plus grand que K*. En utilisant l'action
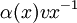 à la place de
à la place de 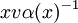 ne fait pas de différence : elle produit le même groupe de Clifford avec la même action sur V.
ne fait pas de différence : elle produit le même groupe de Clifford avec la même action sur V.Le groupe de Clifford
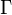 est l'union disjointe de deux sous-ensemble
est l'union disjointe de deux sous-ensemble 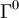 et
et 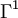 , où
, où 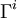 est le sous-ensemble des éléments de degré i. Le sous-ensemble
est le sous-ensemble des éléments de degré i. Le sous-ensemble 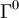 est un sous-groupe d'index 2 dans
est un sous-groupe d'index 2 dans 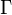 .
.Si V est de dimension finie avec une forme bilinéaire non dégénérée alors les applications du groupe de Clifford sur le groupe orthogonal de V et le noyau consiste en éléments différents de zéro du corps K. Ceci conduit aux suites exactes
En caractéristique arbitraire, la norme de spin Q est définie sur le groupe de Clifford par
C'est un homomorphisme du groupe de Clifford vers le groupe K* des éléments différents de zéro de K. Il coïncide avec la forme quadratique Q de V lorsque V est identifié avec un sous-espace d'algèbre de Clifford. Plusieurs auteurs définissent la norme de spin légèrement différemment, c’est-à-dire qu'elle diffère de celle utilisée ici par un facteur de - 1, 2, ou - 2 sur
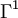 . La différence n'est pas très importante.
. La différence n'est pas très importante.Les éléments différents de zéro de K ont une norme de spin dans le groupe K*2 de carrés des éléments différents de zéro du corps K. Donc, lorsque V est de dimension finie et non-singulière, nous obtenons une application induite à partir du groupe orthogonal de V vers le groupe K*/K*2, aussi appelé la norme de spin. La norme de spin d'une réflexion d'un vecteur r possède comme imge Q(r) dans K*/K*2, et cette propriété le définit uniquement dans le groupe orthogonal. Ceci donne les suites exactes :
Note : En caractéristique 2, le groupe {±1} possède simplement un élément.
Spin et groupes de Pin
Dans cette partie, nous supposons que V est de dimension finie et sa forme bilinéaire non-singulière. (Si K est de caractéristique 2, ceci implique que la dimension de V est pair).
Le groupe de Pin PinV(K) est le sous-groupe du groupe de Clifford
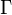 d'éléments de norme de spin 1, et de manière similaire le groupe de Spin SpinV(K) est le sous-groupe d'éléments d'invariant Dickson 0 dans PinV(K). Lorsque la caractéristique n'est pas 2, ceux-ci sont les éléments de déterminant 1. Le groupe de Spin possède généralement un index 2 dans le groupe de Pin.
d'éléments de norme de spin 1, et de manière similaire le groupe de Spin SpinV(K) est le sous-groupe d'éléments d'invariant Dickson 0 dans PinV(K). Lorsque la caractéristique n'est pas 2, ceux-ci sont les éléments de déterminant 1. Le groupe de Spin possède généralement un index 2 dans le groupe de Pin.Rapellons, à partir de la partie précédente, qu'il existe un homomorphisme à partir du groupe de Clifford sur le groupe orthogonal. Nous définissons le groupe spécial orthogonal comme étant l'image de
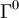 . Si K n'est pas de caractéristique 2, ceci est simplement le groupe d'éléments du groupe orthogonal de déterminant 1. Si K est de caractéristique 2, alors tous les éléments du groupe orthogonal sont de déterminant 1, et le groupe spécial orthogonal est l'ensemble d'éléments d'invariant de Dickson 0.
. Si K n'est pas de caractéristique 2, ceci est simplement le groupe d'éléments du groupe orthogonal de déterminant 1. Si K est de caractéristique 2, alors tous les éléments du groupe orthogonal sont de déterminant 1, et le groupe spécial orthogonal est l'ensemble d'éléments d'invariant de Dickson 0.Il existe un homomorphisme à partir du groupe de Pin vers le groupe orthogonal. L'image est constituée des éléments de norme de spin 1 ∈ K*/K*2. Le noyau est constitué des éléments +1 et -1, et est d'ordre 2 à moins que K soit de caractéristique 2. De manière similaire, il existe un homomorphisme à partir du groupe de Spin vers le groupe spécial orthogonal de V.
Dans le cas courant, lorsque V est un espace défini positif ou négatif sur les réels, le groupe de spin s'applique sur le groupe spécial orthogonal, et est simplement connexe lorsque V est de dimension au moins égale à 3. Attention : Ceci n'est pas vrai en général : si V est
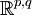 pour p et q tous deux au moins égal à 2, alors le groupe de spin n'est pas simplement connexe et ne s'applique pas sur le groupe spécial orthogonal. Dans ce cas, le groupe algébrique Spinp,q est simplement connexe comme un groupe algébrique, quoique sont groupe de points à valeurs réelles Spinp,q(R) n'est pas simplement connexe. Ceci est plutôt un point subtil, qui a complètement embrouillé les auteurs d'au moins un livre sur les groupes de spin.
pour p et q tous deux au moins égal à 2, alors le groupe de spin n'est pas simplement connexe et ne s'applique pas sur le groupe spécial orthogonal. Dans ce cas, le groupe algébrique Spinp,q est simplement connexe comme un groupe algébrique, quoique sont groupe de points à valeurs réelles Spinp,q(R) n'est pas simplement connexe. Ceci est plutôt un point subtil, qui a complètement embrouillé les auteurs d'au moins un livre sur les groupes de spin.Voir groupe spineur, spineur.
Spineurs
Supposons que p+q=2n est pair. Alors l'algèbre de Clifford
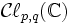 est une algèbre de matrices, et donc possède une représentation complexe de dimension
est une algèbre de matrices, et donc possède une représentation complexe de dimension  . En restreignat au groupe Pinp,q(R) nous obtenons une représentation complexe du groupe Pin de même dimension, appelé la représentation de spin. Si nous restreignons ceci au groupe de spin Spinp,q(R) alors il se sépare en une somme de deux représentations de demi-spin (ou représentations de Weyl ) de dimension
. En restreignat au groupe Pinp,q(R) nous obtenons une représentation complexe du groupe Pin de même dimension, appelé la représentation de spin. Si nous restreignons ceci au groupe de spin Spinp,q(R) alors il se sépare en une somme de deux représentations de demi-spin (ou représentations de Weyl ) de dimension 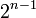 .
.Si p+q=2n+1 est impair alors l'algèbre de Clifford
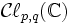 est une somme de deux algèbres de matrices, chacune d'elles possède une représentation de dimension
est une somme de deux algèbres de matrices, chacune d'elles possède une représentation de dimension  , et celles-ci sont aussi toutes deux des représentations du groupe de Pin Pinp,q(R). Sur la restriction au groupe de spin Spinp,q(R), celles-ci deviennent isomorphes, donc le groupe de spin possède une représentation de spin complexe de dimension
, et celles-ci sont aussi toutes deux des représentations du groupe de Pin Pinp,q(R). Sur la restriction au groupe de spin Spinp,q(R), celles-ci deviennent isomorphes, donc le groupe de spin possède une représentation de spin complexe de dimension  .
.Plus généralement, les groupes de spin et les groupes de pin sur tout corps ont des représentations similaires dont la structure exacte dépend de la structure des algèbres de Clifford correspondantes : toutes les fois qu'une algèbre de Clifford possède un facteur qui est une algèbre de matrice sur certaines algèbre de division, nous obtenons une représentation correspondante des groupes de spin et de pin sur cette algèbre de division. Pour des exemples sur les réels :
Article détaillé : spineur.Applications
Géométrie différentielle
En géométrie différentielle, on utilise couramment les notions d'algébre extérieure pour définir par exemple le fibré vectoriel des formes différentielles sur une variété différentielle. Dans le cas d'une variété (pseudo-)riemannienne, les espaces tangents sont munis d'une forme quadratique naturelle induite par la métrique. Ainsi, on peut définir un "fibré vectoriel" de Clifford en analogie avec le fibré vectoriel extérieur. Cette construction offre d'intéressantes applications en géométrie riemannienne.
Physique
Les algèbres de Clifford ont de nombreuses applications importantes en physique. Les physiciens considèrent habituellement une algèbre de Clifford comme une algèbre engendrée par des matrices
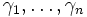 appelées matrices de Dirac qui ont la propriété :
appelées matrices de Dirac qui ont la propriété :où
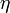 est la matrice d'une forme quadratique de signature (p,q) — typiquement (1,3) lorsqu'on travaille dans un espace de Minkowski. Celles-ci sont exactement les relations définies pour l'algèbre de Clifford
est la matrice d'une forme quadratique de signature (p,q) — typiquement (1,3) lorsqu'on travaille dans un espace de Minkowski. Celles-ci sont exactement les relations définies pour l'algèbre de Clifford 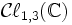 (à un facteur 2 sans importance près), qui par la classification des algèbres de Clifford est isomorphe à l'algèbre de matrices complexes 4 x 4. Les matrices γi ne sont que les matrices de la multiplication par le vecteur ei dans la représentation spinorielle, par rapport à une base arbitraire de spineurs.
(à un facteur 2 sans importance près), qui par la classification des algèbres de Clifford est isomorphe à l'algèbre de matrices complexes 4 x 4. Les matrices γi ne sont que les matrices de la multiplication par le vecteur ei dans la représentation spinorielle, par rapport à une base arbitraire de spineurs.Les matrices de Dirac furent découvertes en premier par Paul Dirac lorsqu'il essaya d'écrire une équation d'onde du premier ordre relativiste pour l'électron, et donna un isomorphisme explicite de l'algèbre de Clifford vers l'algèbre des matrices complexes. Le résultat fut utilisé pour définir l'équation de Dirac. L'algèbre de Clifford entière est utilisée dans la théorie des champs quantiques sous la forme des corps de Dirac bilinéaires.
Voir aussi
- Algèbre de l'espace physique
- Classification des algèbres de Clifford
- Représentation des algèbres de Clifford
- Matrice de Dirac
- Algèbre extérieure
- Algèbre géométrique
- Groupe de spin
- Spineur
- Paravecteur
Notes de bas de page
-
Les mathématiciens qui travaillent avec les algèbres de Clifford réelles et préfèrent des formes quadratiques définies positives (précisément ceux travaillant dans la théorie de l'indice) utilisent quelquefois un choix de signe différent dans l'identité fondamentale de Clifford. C’est-à-dire qu'ils prennent
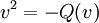 . On peut remplacer Q par - Q en allant d'une convention à l'autre.
. On peut remplacer Q par - Q en allant d'une convention à l'autre. -
L'opposé est vrai lorsque la convention de signe alternative (-) pour les algèbres de Clifford est utilisée : c'est le conjugué qui est plus important. En général, les significations de la conjugaison et de la transposition sont interchangées lorsque l'on passe d'une convention de signe à une autre. Par exemple, dans la convention utilisée ici, l'inverse d'un vecteur est donné par
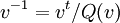 tandis que dans la convention (-), il est donné par
tandis que dans la convention (-), il est donné par 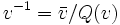 .
.
Références
- Carnahan, S. Borcherds Seminar Notes, Uncut. Week 5, "Spinors and Clifford Algebras".
- Lawson and Michelsohn, Spin Geometry, Princeton University Press. 1989. ISBN 0-691-08542-0. An advanced textbook on Clifford algebras and their applications to differential geometry.
- Lounesto, P., Clifford Algebras and Spinors, Cambridge University Press. 2001. ISBN 0-521-00551-5.
- Porteous, I., Clifford Algebras and the Classical Groups, Cambridge University Press. 1995. ISBN 0-521-55177-3.
Liens externes
- Entrée sur Planetmath pour les algèbres de Clifford
- Une histoire d'algèbres de Clifford (non vérifié)
- Portail des mathématiques
Catégories : Algèbre multilinéaire | Structure externe
Wikimedia Foundation. 2010.