- Systeme dynamique
-
Système dynamique
Pour consulter un article plus général, voir : Systèmes dynamiques.En mathématiques, en physique théorique et en ingénierie, un système dynamique est un système classique[1] qui évolue au cours du temps de façon à la fois :
- causale, c’est-à-dire que son avenir ne dépend que de phénomènes du passé ou du présent ;
- déterministe, c’est-à-dire qu'à une « condition initiale » donnée à l'instant « présent » va correspondre à chaque instant ultérieur un et un seul état « futur » possible.
On exclut donc ici conventionnellement les systèmes « bruités » intrinsèquement stochastiques, qui relèvent de la théorie des probabilités.
L'évolution déterministe du système dynamique peut alors se modéliser de deux façons distinctes :
- une évolution continue dans le temps, représentée par une équation différentielle ordinaire. C'est a priori la plus naturelle physiquement, puisque le paramètre temps nous semble continu.
- une évolution discontinue dans le temps. Ce second cas est souvent le plus simple à décrire mathématiquement, même s'il peut sembler a priori moins réaliste physiquement[2]. Cependant, l'étude théorique de ces modèles discrets est fondamentale, car elle permet de mettre en évidence des résultats importants, qui se généralisent souvent aux évolutions dynamiques continues.
Sommaire
Système dynamique à temps discret
Notion d'état dynamique : aspect philosophique
Il faut faire attention au sens très particulier que prend la notion d’état pour la théorie des systèmes dynamiques. Un paradoxe de Zénon permet de présenter la difficulté. Zénon demandait : « Soit une flèche en vol. À un instant, est-ce qu’elle est au repos ou en mouvement ? » Si on répondait qu’elle est en mouvement, il disait « Mais être en mouvement, c’est changer de position. À un instant, la flèche a une position, elle n’en change pas. Elle n’est donc pas en mouvement. » Si on répondait qu’elle est au repos, il disait « Mais si elle est au repos à cet instant, elle est aussi au repos à tous les autres instants, elle est donc toujours au repos. Elle n’est jamais en mouvement. Mais comment alors peut-elle passer d’une position à une autre ? » Il en concluait qu’il n’est pas possible de dire des vérités sur ce qui est en mouvement. Tout ce qui est en mouvement serait par nature mensonger et il n’y aurait pas de vérités à propos de la matière mais seulement à propos des grandes idées, pourvu qu’elles soient immuables. Le sens commun est exactement inverse. On croit plus couramment à la vérité de ce qu’on voit qu’aux vérités métaphysiques. La théorie des systèmes dynamiques rejoint le sens commun sur ce point.
La notion d’état dynamique fournit une solution au paradoxe de Zénon : à un instant, la flèche est en mouvement, elle a une position mais elle est en train de changer de position, elle a une vitesse instantanée. Les nombres qui mesurent sa position et sa vitesse sont les valeurs de ses variables d’état. Les variables d’état sont toutes les grandeurs physiques qui déterminent l’état instantané du système et qui ne sont pas constantes a priori. On les appelle aussi les variables dynamiques. Si on prend une photo au flash on ne voit pas que la flèche est en mouvement, mais on peut le détecter par d’autres moyens, par l’effet Doppler par exemple, sans avoir à mesurer un changement de position. L’état dynamique d’un système est un état instantané, mais c’est un état de mouvement. Il est déterminé par les valeurs de toutes les variables d’état à cet instant.
Espace des phases
Pour un système possédant n degrés de liberté, l'espace des phases Γ du système possède n dimensions, de telle sorte que l'état complet
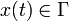 du système à l'instant t est en général un vecteur à n composantes.
du système à l'instant t est en général un vecteur à n composantes.Dynamique discrète
Un système dynamique discret est défini par une application bijective
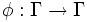 de l'espace des phases sur lui-même. Elle opère de la façon suivante : étant donnée une condition initiale x0 de l'état du système, le premier état suivant est :
de l'espace des phases sur lui-même. Elle opère de la façon suivante : étant donnée une condition initiale x0 de l'état du système, le premier état suivant est :
Le second état, qui suit immédiatement le premier, est :
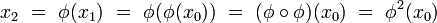
et ainsi de suite, de telle sorte que le n-ième état est donné par :
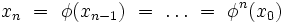
Pour remonter dans le passé, il suffit d’inverser la fonction φ, ce qui est toujours possible pour une bijection [3].
Classification des dynamiques
On distingue plusieurs grands types de dynamiques en fonction de la nature mathématique de l'espace des phases :
- lorsque Γ est un espace topologique et l'application
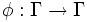 un homéomorphisme, on parle de dynamique topologique.
un homéomorphisme, on parle de dynamique topologique.
- lorsque Γ est une variété différentielle et l'application
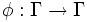 un difféomorphisme, on parle de dynamique différentielle.
un difféomorphisme, on parle de dynamique différentielle.
- lorsque Γ est un espace mesurable et
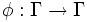 une application qui préserve la mesure, on entre dans le domaine de la théorie ergodique, et on parle de système dynamique mesuré
une application qui préserve la mesure, on entre dans le domaine de la théorie ergodique, et on parle de système dynamique mesuré
Exemples
La fonction logistique
Article détaillé : suite logistique.La fonction logistique est une application du segment [0, 1] dans lui-même qui sert de récurrence à la suite :
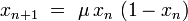
où n = 0, 1, ... dénote le temps discret, x l'unique variable dynamique, et
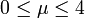 un paramètre[4].
un paramètre[4].La dynamique de cette application présente un comportement très différent selon la valeur du paramètre μ :
- Pour
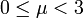 , le système possède un point fixe attractif, qui devient instable lorsque μ = 3.
, le système possède un point fixe attractif, qui devient instable lorsque μ = 3.
- Pour
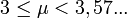 , l'application possède un attracteur qui est une orbite périodique, de période 2n où n est un entier qui tend vers l'infini lorsque μ tend vers 3,57 ...
, l'application possède un attracteur qui est une orbite périodique, de période 2n où n est un entier qui tend vers l'infini lorsque μ tend vers 3,57 ...
- Lorsque μ = 3,57..., l'application possède un attracteur de Feigenbaum fractal (mais non étrange) découvert par May (1976)[5].
- Le cas μ = 4 avait été étudié dès 1947 par Ulam et von Neumann [6]. On peut dans ce cas précis établir l'expression exacte de la mesure invariante ergodique [7].
On obtient donc une succession de bifurcations de la régularité vers le chaos lorsque le paramètre augmente, résumée sur la figure ci-jointe.
L'application « chat » d'Arnold (1968)
Le nom d'application « chat » provient d'un jeu de mot anglais intraduisible en français : en effet, « chat » se dit « cat » en anglais, et Arnold utilisait ce mot comme abréviation de : « Continuous Automorphisms of the Torus », littéralement : « automorphismes continus sur le tore ».
L'application « chat » [8] est une application du carré [0, 1] x [0, 1] dans lui-même définie par :
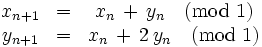
où mod 1 signifie : modulo 1. Cette condition entraine que le carré [0, 1] x [0, 1] voit ses bords recollés deux à deux pour former le « tore » du titre. Il s'agit d'un système dynamique conservatif, qui préserve la mesure de Lebesgue dx dy.
L'application de Hénon (1976)
L'application de Hénon[9] est une bijection du carré [0, 1] x [0, 1] dans lui-même définie par :
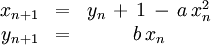
où a et b sont deux paramètres, dont des valeurs typiques sont a = 1,4 et b = 0,3. Avec ces valeurs, la dynamique présente un attracteur étrange de nature fractale, de type Cantor[10].
Hénon a obtenu ses équations en cherchant une version simplifiée du système dynamique de Lorenz à temps continu introduit en 1963 (cf. plus bas). Le système dynamique de Hénon n'est pas conservatif, car le jacobien de la transformation est constant[11] et vaut - b, qui est différent de l'unité dans les cas intéressants.
Autres exemples
- La dynamique holomorphe, où l'espace des phases est le plan complexe
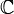 et φ une application holomorphe. Une telle dynamique est par exemple à l'origine de l'ensemble de Mandelbrot.
et φ une application holomorphe. Une telle dynamique est par exemple à l'origine de l'ensemble de Mandelbrot.
- La percolation
Système dynamique différentiel
Depuis Newton (1687), l'idée que l'évolution temporelle d'un système physique quelconque est bien modélisée par une équation différentielle (ou ses généralisations à la théorie des champs, les équations aux dérivées partielles) est admise. Cette modélisation différentielle s'est depuis étendue avec succès à d'autres disciplines comme la chimie, la biologie, l'économie, ...
Pour un système possédant n degrés de liberté, l'espace des phases Γ du système possède n dimensions, de telle sorte que l'état complet
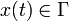 du système à l'instant t est en général un vecteur à n composantes. On considère alors typiquement un système différentiel du premier ordre du type[12] :
du système à l'instant t est en général un vecteur à n composantes. On considère alors typiquement un système différentiel du premier ordre du type[12] :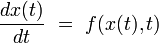
où la fonction f définit le système dynamique étudié (c'est en général également un vecteur à n dimensions, c’est-à-dire un ensemble de n fonctions scalaires).
Problème de Cauchy
On se pose la question suivante, appelée problème de Cauchy : étant donnée une condition initiale x0 représentant l'état complet du système physique dans son espace des phases à un instant initial t0, trouver l'état complet du système x(t) dans son espace des phases pour tout instant ultérieur t > t0. La solution à ce problème fondamental réside dans le théorème de Cauchy-Lipschitz, qui assure l'existence locale et l'unicité de la solution d'une équation différentielle.
Déterminisme
L’hypothèse que l’avenir est déterminé par le présent est très audacieuse. Son succès n’est pas a priori évident. Pourtant toutes les grandes théories fondamentales de la physique l’ont adoptée, à la suite de Newton.
Article détaillé : Déterminisme.Déterminisme d'un système conservatif
Nous conviendrons de dire qu'un système physique conservatif est déterministe si et seulement si la dynamique du système associe à chaque condition initiale x0 un et un seul état final x(t). Il faut pour cela qu'il existe une application bijective
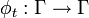 de l'espace des phases sur lui-même telle que :
de l'espace des phases sur lui-même telle que :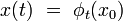
Lorsque le temps t varie, cette bijection engendre un flot sur Γ, c’est-à-dire un groupe continu à un paramètre φt tel que :
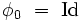

Cette description correspond par exemple au flot hamiltonien de la mécanique classique, ainsi qu'au flot géodésique.
Cas d'un système non-conservatif
Lorsque le système physique considéré est non-conservatif, l'application φt n'est pas bijective[13], et il existe en général un (ou plusieurs) attracteur dans l'espace des phases du système, c’est-à-dire un sous-ensemble de l'espace des phases invariant sous φt vers lequel converge le point représentatif x(t) du système lorsque le temps t tend vers l'infini, et ce pour presque toute condition initiale x0.
Exemples
L'oscillateur de Van der Pol (1928)
Article détaillé : Oscillateur de Van der Pol.L'oscillateur de van der Pol libre (i.e. sans excitation extérieure) est un système à un degré de liberté, décrit par la coordonnée x(t), qui possède deux paramètres :
- une pulsation ω0
- un coefficient de non-linéarité ε.
Son équation différentielle s'écrit[14] :
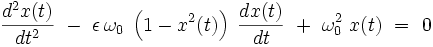
Ce système dissipatif possède une dynamique régulière lorsqu'il est libre, caractérisée par un attracteur en forme de cycle limite représenté sur la figure ci-dessous (où on a posé ω0 = 1) :
Le système de Lorenz (1963)
Article détaillé : Système dynamique de Lorenz. Attracteur étrange de Lorenz.
Attracteur étrange de Lorenz.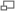
En 1963, Lorenz a proposé un système différentiel possédant trois degrés de liberté[15]., notés x(t), y(t) et z(t), qui s'écrit :
![\frac{dx(t)}{dt} \ = \ \sigma \ \left[ \ y(t) - x(t) \ \right]](/pictures/frwiki/98/beda9b7e28158bdcb1119bba208e0b5b.png)
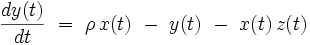
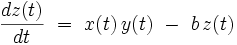
Dans ces équations, σ, ρ et b sont trois paramètres réels. Pour les valeurs suivantes : σ = 10, ρ = 28 et b=8/3, ce système dynamique différentiel présente un superbe attracteur étrange, représenté sur la figure ci-jointe.
Systèmes linéaires et Systèmes non linéaires
Nous distinguons les systèmes dynamiques linéaires des systèmes dynamiques non-linéaires. Dans les premiers, le membre de droite de l'équation est une fonction dépendant linéairement de x, telle que:
La somme de deux solutions d'un système linéaire est également solution (« principe de superposition »). Les solutions d'une équation linéaire forment un espace vectoriel, ce qui permet l'utilisation de l'algèbre linéaire et simplifie considérablement l'analyse. Pour les systèmes à temps continu, la transformée de Laplace permet de transformer les équations différentielles en des équations algébriques.
Les deux premiers exemples donnés plus haut sont des systèmes non linéaires. Leur analyse est en général très difficile. Par ailleurs, les systèmes non linéaires ont souvent des comportements dits chaotiques, ce qui les rend apparemment imprévisibles.
Les systèmes dynamiques et la théorie du chaos
Article détaillé : Théorie du chaos.Des systèmes dynamiques non linéaires, ou simplement linéaires par morceau, peuvent faire preuve de comportements complètement imprévisibles, qui peuvent même sembler aléatoires (alors qu'il s'agit de systèmes parfaitement déterministes). Cette imprédictibilité est appelée chaos. La branche des systèmes dynamiques qui s'attache à définir clairement et à étudier le chaos s'appelle la théorie du chaos.
Cette branche des mathématiques décrit qualitativement les comportements à long terme des systèmes dynamiques. Dans ce cadre, on ne met pas l'accent sur la recherche de solutions précises aux équations du système dynamique (ce qui, de toute façon, est souvent sans espoir), mais plutôt sur la réponse à des questions comme « Le système convergera-t-il vers un état stationnaire à long terme, et dans ce cas, quels sont les états stationnaires possibles ? » ou « Le comportement à long terme du système dépend-il des conditions initiales ? ».
Un objectif important est la description des points fixes, ou états stationnaires, du système ; ce sont les valeurs de la variable pour lesquelles elle n'évolue plus avec le temps. Certains de ces points fixes sont attractifs, ce qui veut dire que si le système parvient à leur voisinage, il va converger vers le point fixe.
De même, on s'intéresse aux points périodiques, les états du système qui se répètent au bout d'un certain nombre de pas (leur période). Les points périodiques peuvent également être attractifs. Le théorème de Sarkovskii donne une contrainte sur l'ensemble des périodes possibles des points d'un système dynamique à variable réelle et fonction d'évolution continue ; notamment, s'il existe un point de période 3, il existe des points de période quelconque (« période 3 = chaos »).
Le comportement chaotique de systèmes complexes n'est pas une surprise – on sait depuis longtemps que la météorologie comprend des comportements complexes et même chaotiques. La véritable surprise est plutôt la découverte de chaos dans des systèmes presque triviaux ; ainsi, la fonction logistique est un simple polynôme du second degré, pourtant le comportement de ses solutions est chaotique.
Bibliographie
Ouvrages d'initiation
- John Hubbard et Beverly West ; Équations différentielles et systèmes dynamiques, Cassini (1999), ISBN 284225015X.
- Grégoire Nicolis & Ilya Prigogine ; À la rencontre du complexe, Collection Philosophie d'aujourd'hui, Presses Universitaires de France (1992), ISBN 2-13-043606-4.
- Boris Hasselblatt & Anatole Katok ; A First Course in Dynamics with a Panorama of Recent Developments, Cambridge University Press (2003), ISBN 0521587506.
- Diederich Hinrichsen & Anthony J. Pritchard ; Mathematical Systems Theory. Modelling, State Space Analysis, Stability and Robustness, New York: Springer (2005). ISBN 978-3-540-44125-0
- Anatole Katok & Boris Hasselblatt ; Introduction to the Modern Theory of Dynamical Systems (With a supplément by Anatole Katok and Leonardo Mendoza), Encyclopedia of Mathematics and Its Applications 54, Cambridge University Press (1997), ISBN 0-521-57557-5.
Ouvrages plus techniques
- Steve Smale ; The mathematics of time - Essays on Dynamical Systems, Economic Processes & Related Topics, Springer-Verlag (1980), ISBN 0-387-90519-7.
- Boris Hasselblatt & Anatole Katok (eds.) ; Handbook of Dynamical Systems, Elsevier.
- Vol. 1A (2002), ISBN 0-444-82669-6.
- Vol. 1B (2005), ISBN 0-444-52055-4.
- B. Fiedler (ed.) ; Handbook of Dynamical Systems - Vol. 2: Applications, Elsevier (2002).
- Handbook of Dynamical Systems - Vol. 3: Geometric Methods of Differentiable Dynamics, Elsevier (à paraitre).
- L.A. Bunimovich, S.G. Dani, R.L. Dobrushin, M.V. Jakobson, I.P. Kornfeld, N.B. Maslova, Y.B. Pesin, Y.G. Sinai, J. Smillie, Y.M. Sukhov & A.M Vershik ; Dynamical Systems, Ergodic Theory and Applications, Series: Encyclopaedia of Mathematical Sciences 100, Volume package: Mathematical Physics, Springer-Verlag (2e édition-2000), ISBN 3-540-66316-9.
- Vladimir Damgov, Nonlinear and parametric phenomena. Applications to radiometric and mechanical systems, World Scientific, Series on Nonlinear Sciences, 2004.
Bibliothèque virtuelle
- Paul Manneville ; Systèmes dynamiques et chaos, (1998), 233 pages,. Cours donné par l'auteur (LadHyX, École Polytechnique) aux DEA de Physique des Liquides et de Mécanique. Texte complet disponible ici.
- David Ruelle ; Ergodic theory of differentiable dynamical systems, Publications Mathématiques de l'IHÉS 50 (1979), 27-58. Texte complet disponible au format pdf.
Notes
- ↑ Classique est ici utilisé au sens de non-quantique.
- ↑ On peut en fait toujours associer une (ou plusieurs) dynamique(s) discrète(s) à une dynamique continue donnée en échantillonnant l'état du système à une suite d'instants
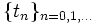 , chaque choix de discrétisation du temps produisant a priori un échantillonnage différent.
, chaque choix de discrétisation du temps produisant a priori un échantillonnage différent. - ↑ Quand on apprend en mathématiques à inverser des fonctions, on apprend à fabriquer une sorte de machine à remonter le temps.
- ↑ Lorsque le paramètre μ devient supérieur à quatre, l'application sort de l'intervalle [0, 1].
- ↑ R.M. May ; Nature 261 (1976), 459.
- ↑ Stanislas Ulam & John Von Neumann ; Bulletin of the American Mathematical Society 53 (1947), 1120.
- ↑ Pierre Collet & Jean-Pierre Eckmann ; Iterated Maps on the Interval as Dynamical Systems, Birkhaüser (1980).
- ↑ Vladimir I. Arnold & André Avez ; Ergodic Problems of Classical Mechanics, (1968). Réédition : Advanced Book Classics, Pearson Addison Wesley (Mai 1989), ASIN 0201094061.
- ↑ Michel Hénon ; A two-dimensionnal mapping with a strange attractor, Communication in Mathematical Physics 50 (1976), 69. Disponible au format pdf. Lire également : James H. Curry ; On the Henon transformation, Communication in Mathematical Physics 68 (1979), 129. Disponible au format pdf.
- ↑ Avec a = 1,3 et b = 0,3, l'attracteur étrange disparait totalement au profit d'un attracteur en forme d'orbite périodique, de période 7.
- ↑ Ce type d'application polynomiale de jacobien constant est appelée « transformation entière de Cremona ». Cf. Wolfgang Engel ; Ein Satz über ganze Cremona-Transformationen der Ebene, Mathematische Annalen 130 (1955), 11 et : Ganze Cremona-Transformationen von Primzahlgrad in der Ebene, Mathematische Annalen 136 (1958), 319.
- ↑ Rappelons qu'une équation différentielle d'ordre n peut toujours se ramener à un système de n équations différentielles couplées d'ordre un.
- ↑ En particulier, l'application φt n'admet pas d'inverse
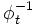 .
. - ↑ Introduit en 1928, cet oscillateur à relaxation a été introduit pour la modélisation des battements du cœur humain ; cf. Balth. van der Pol & J van der Mark ; The Heartbeat considered as a Relaxation oscillation, and an Electrical Model of the Heart, Philosophical Magazine Supplement 6 (1928), 763-775.
- ↑ Edward N. Lorenz, Deterministic non-periodic flow, Journal of the Atmospheric Sciences 20(2) (1963), 130–141. Format pdf.
Articles connexes
- Attracteur
- Équation différentielle ordinaire
- Équation aux dérivées partielles
- Mécanique hamiltonienne
- Système intégrable
- Systèmes dynamiques (article doublon)
- Théorème KAM
- Théorie ergodique
- Théorie du chaos
- Théorie du contrôle
Liens externes
- Émergence du chaos
- Itérations dans l'ensemble de Mandelbrot
- Modèle logistique
- Introduction to Social Macrodynamics
- Nouveau logiciel français de dynamique des systèmes
- Portail des mathématiques
- Portail de la physique
Catégories : Dynamique | Ingénierie | Systèmes dynamiques
Wikimedia Foundation. 2010.



