- K3 (mathématiques)
-
K3 (géométrie)
 Pour les articles homonymes, voir K3.
Pour les articles homonymes, voir K3.En géométrie différentielle ou algébrique, l'espace K3, ou encore la surface K3, est la variété de Calabi-Yau de plus petite dimension différent d'un tore. C'est une variété complexe de dimension complexe 2[1] compacte et Kähler.
La surface K3 possède en outre la propriété d'être l'unique variété de Calabi-Yau distincte du 4-tore
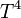 d'un point de vue topologique ou différentiel. Cependant, en tant que variété complexe, il y a un nombre infini de surfaces K3 non isomorphes. On peut notamment les distinguer par le biais du morphisme de Torrelli.
d'un point de vue topologique ou différentiel. Cependant, en tant que variété complexe, il y a un nombre infini de surfaces K3 non isomorphes. On peut notamment les distinguer par le biais du morphisme de Torrelli.Sommaire
Caractéristiques géométrique
La plupart des surfaces K3 ne sont pas des variétés algébriques. Ceci signifie qu'il est en général impossible de les réaliser comme l'ensemble des solutions d'équations polynomiales dans un espace projectif.
Cependant, ces surfaces sont d'abord apparues en géométrie algébrique et leur nom provient des trois géomètres Kummer, Kähler et Kodaira.
Le groupe de cohomologie
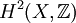 est un groupe abélien libre de rang 22. Il est muni (par le produit en cohomologie) d'une forme quadratique non dégénérée de signature (3,19). En tant que réseau, ce groupe de cohomologie contient deux facteurs de type E8. On peut décrire explicitement la base orthogonale pour cette forme quadratique en considérant le diamant de Hodge pour K3 qui s'écrit
est un groupe abélien libre de rang 22. Il est muni (par le produit en cohomologie) d'une forme quadratique non dégénérée de signature (3,19). En tant que réseau, ce groupe de cohomologie contient deux facteurs de type E8. On peut décrire explicitement la base orthogonale pour cette forme quadratique en considérant le diamant de Hodge pour K3 qui s'écrit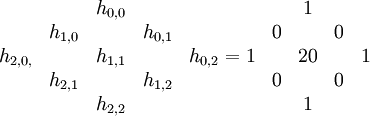
où hi,j sont les dimensions des espaces de cohomologie de Dolbeault. Par ailleurs parmi les 20 (1,1)-formes, 19 sont selfduales avec une norme positive tandis que la (1,1) forme restante, accompagnée de la (2,0) et de la (0,2) formes sont anti-selfduales et possèdent une norme négative.
Comme tous les Calabi-Yau non-triviaux, on ne connaît pas à ce jour de métrique Ricci-plate explicite bien que son existence soit assurée par le théorème de Yau.
Utilisation en théorie des cordes
Cet espace est souvent utilisé comme espace de compactification en théorie des supercordes. Dans ce contexte, la surface K3 fait une apparition remarquable dans la dualité corde-corde qui affirme que la théorie de type IIA compactifiée sur la surface K3 est équivalente à la corde hétérotique compactifiée sur un tore à quatre dimensions.
Bibliographie
- (en) Paul Aspinwall, K3 Surfaces and String Duality, disponible sur l'arXiv.
- (en) David Morrison, The Geometry of K3 surfaces[pdf],
Notes
- ↑ D'où le nom de surface. En tant que variété réelle, elle possède une dimension 4
Voir aussi
- Théorie des supercordes
- Compactification
- Orbifold
- Dualité de corde
- Variété complexe
- Variété hyperkähler
- Portail de la géométrie
- Portail de la physique
Catégories : Théorie des cordes | Géométrie algébrique | Géométrie différentielle
Wikimedia Foundation. 2010.
