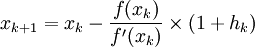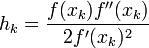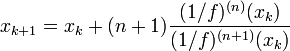Itération de householder
- Itération de householder
-
Itération de Householder
En analyse numérique, l'itération de Householder ou méthode de Householder désigne un algorithme de recherche d'un zéro d'une fonction utilisé pour les fonctions d'une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).
L'algorithme est itératif et de convergence cubique ; il se généralise à des fonctions Cn avec une convergence d'ordre n + 1.
Il doit son nom à son inventeur, le mathématicien Alston Scott Householder.
Énoncé
Soit f une fonction C² et a un zéro de f. La méthode de Householder consiste à itérer :
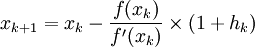
avec
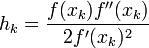
à partir d'une estimation x0 de a.
On retrouve l'itération de Halley en remplaçant (1 + hk) par 1/(1 − hk) pour hk << 1 dans la relation de récurrence ci-dessus.
Généralisation
Les méthodes Householder généralisent la méthode de Newton (cas n = 0) et la méthode de Halley (cas n = 1) dans le cas d'une fonction Cn + 1 :
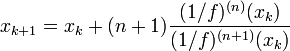
Leur vitesse de convergence est d'ordre n + 2.
Voir aussi
Liens internes
Liens externes
Bibliographie
- (en) Alston Scott Householder, Numerical Treatment of a Single Nonlinear Equation, McGraw Hill Text, New York, 1970. ISBN 0-07-030465-3
 Portail des mathématiques
Portail des mathématiques
Catégorie : Algorithme de recherche d'un zéro d'une fonction
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Itération de householder de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Iteration de Householder — Itération de Householder En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée… … Wikipédia en Français
Itération De Householder — En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).… … Wikipédia en Français
Itération de Householder — En analyse numérique, l itération de Householder ou méthode de Householder désigne un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2).… … Wikipédia en Français
Iteration de Halley — Itération de Halley En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e … Wikipédia en Français
Itération De Halley — En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2). L algorithme… … Wikipédia en Français
Itération de Halley — En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2). L algorithme… … Wikipédia en Français
Itération de halley — En analyse numérique, l itération de Halley ou méthode de Halley est un algorithme de recherche d un zéro d une fonction utilisé pour les fonctions d une variable réelle dérivables deux fois et à dérivée seconde continue (i.e. C2). L algorithme… … Wikipédia en Français
Householder's method — In numerical analysis, the class of Householder s methods are root finding algorithms used for functions of one real variable with continuous derivatives up to some order d+1 , where d will be the order of the Householder s method.The algorithm… … Wikipedia
Householder-Verfahren — Die Householder Verfahren sind eine Gruppe von numerischen Verfahren zur Bestimmung von Nullstellen einer skalaren reellen Funktion. Sie sind nach Alston Scott Householder benannt. Inhaltsverzeichnis 1 Beschreibung des Verfahrens 2 Motivation 3… … Deutsch Wikipedia
Racine carrée de deux — La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10 9… … Wikipédia en Français