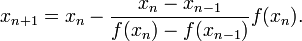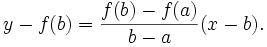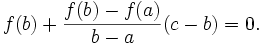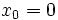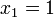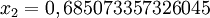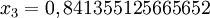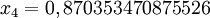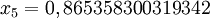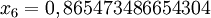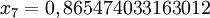- Methode de la secante
-
Méthode de la sécante
En analyse numérique, la méthode de la sécante est un algorithme de recherche de racines d'une fonction f.
Sommaire
La méthode
La méthode de la sécante est une méthode dérivée de celle de Newton où l'on remplace
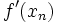 par
par 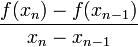 On obtient la relation de récurrence
On obtient la relation de récurrenceL'initialisation nécessite 2 points x0 et x1, proches, si possible, de la solution recherchée.
Démonstration
 La courbe rouge représente la fonction f et le segment en bleu, la sécante.
La courbe rouge représente la fonction f et le segment en bleu, la sécante.Étant donné a et b, on construit le segment reliant (a, f(a)) et (b, f(b)). La droite peut être définie ainsi :
On choisit c de telle sorte que c soit la racine de cette droite (c'est-à-dire f(c) =0)
Si on extrait c de cette équation, on retrouve la relation de récurrence citée plus haut.
Convergence
Si les valeurs initiales de x0 et de x1 sont suffisamment proches de la solution, la méthode aura un ordre de convergence de
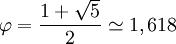 qui est le nombre d'or.
qui est le nombre d'or.
Toutefois, la fonction f doit être 2 fois continuement différentiable et ce doit être une racine simple.
Exemples d'implémentation
Ce programme en C résout le problème f(x) = cos(x) - x3 = 0. Les tests d'arrêts sont les suivants :
- | xn + 1 − xn | < e
- n > m
m et e étant donnés.
#include <stdio.h> #include <math.h> double f(double x) { return cos(x) - x*x*x; } double SecantMethod(double xn_1, double xn, double e, int m) { int n; double d; for (n = 1; n <= m; n++) { d = (xn - xn_1) / (f(xn) - f(xn_1)) * f(xn); if (fabs(d) < e) return xn; xn_1 = xn; xn = xn - d; } return xn; } int main(void) { printf("%0.15f\n", SecantMethod(0, 1, 5E-11, 100)); return 0; }On obtient les résultats suivants :
Programme en Fortran :PROGRAM MethodeSecante IMPLICIT NONE REAL(8) :: Secante, f ! Fonctions REAL(8) :: x x=Secante(0d0, 1d0, 5d-11) PRINT *, x, f(x) END PROGRAM MethodeSecante REAL(8) FUNCTION f(x) IMPLICIT NONE REAL(8) :: x f=cos(x) - x*x*x END FUNCTION f REAL(8) FUNCTION Secante(x0, x1, e) IMPLICIT NONE REAL(8) :: f ! Fonction REAL(8) :: x0,x1,xn_1,xn REAL(8) :: d,e d=2d0*e xn_1=x0 xn=x1 DO WHILE (ABS(d)>e) d = (xn - xn_1) / (f(xn) - f(xn_1)) * f(xn) xn_1 = xn xn = xn - d END DO Secante=xn END FUNCTION SecanteVoir aussi
- Portail des mathématiques
Catégorie : Algorithme de recherche d'un zéro d'une fonction
Wikimedia Foundation. 2010.