- Methode de Newton
-
Méthode de Newton
En analyse numérique, la méthode de Newton, ou méthode de Newton-Raphson[1], est un algorithme efficace pour trouver des approximations d'un zéro (ou racine) d'une fonction d'une variable réelle à valeurs réelles. L'algorithme consiste à linéariser une fonction f en un point et de prendre le point d'annulation de cette linéarisation comme approximation du zéro recherché. On réitère cette procédure en l'approximation obtenue. Dans les cas favorables, les approximations successives obtenues convergent avec une vitesse quadratique. De manière informelle, le nombre de décimales correctes double à chaque étape.
Appliqué à la dérivée d'une fonction, cet algorithme permet d'obtenir une évaluation des points critiques. La méthode de Newton se généralise en dimension supérieure. La raison réside en une utilisation du théorème du point fixe, qui cependant n'est pas nécessaire pour comprendre le sens du résultat.
Cette méthode porte le nom des mathématiciens anglais Isaac Newton (1643-1727) et Joseph Raphson, qui furent les premiers à la décrire pour l'appliquer à la recherche des zéros d'une équation polynomiale.
Sommaire
Pour les fonctions d'une variable réelle
Histoire
La méthode de Newton fut décrite de manière satisfaisante par le mathématicien anglais Isaac Newton (1643-1727) dans De analysi per aequationes numero terminorum infinitas, écrit en 1669 et publié en 1711 par William Jones (1675-1749). Elle fut à nouveau décrite dans De metodis fluxionum et serierum infinitarum (De la méthode des fluxions et des conséquences infinies), écrit en 1671, traduit et publié sous le titre Methods of Fluxions en 1736 par John Colson. Toutefois, Newton n'appliqua la méthode qu'aux seuls polynomes. Comme la notion de dérivée et donc de linéarisation n'était pas définie à cette époque, l'approche adoptée diffère : Newton cherchait à affiner une approximation grossière d'un zéro d'un polynome par un calcul polynomial.
Par exemple, 2 est un zéro exact de X3 − 2X2 − 3X + 6 et donc peut être pris comme un zéro approximatif de P(X) = X3 − 2X2 − 3X + 7. Une petite perturbation doit s'écrire 2 + Y. Or, P(2 + Y) = 1 − 7Y + 2Y2 + Y3 = 1 − 7Y en négligeant les termes d'ordre au moins 2. L'annulation de P par 2 + Y impose Y = 1 / 7.
Cette méthode fut l'objet de publications antérieures. En 1685, John Wallis (1616-1703) en publia une première description dans A Treatise of Algebra both Historical and Practical. En 1690, Joseph Raphson en publia une description simplifiee dans Analysis aequationum universalis. Raphson considérait la méthode de Newton toujours comme une méthode purement algébrique et restreignait aussi son usage aux seuls polynomes. Toutefois, il mit en évidence le calcul récursif des approximations successives d'un zéro d'un polynome au lieu de considérer comme Newton une suite de polynomes.
Ce n'est qu'en 1740 que Thomas Simpson (1710-1761) décrivit cette méthode de calcul itératif pour approcher les solutions d'une équation non linéaire, utilisant le calcul fluxionnel. Simpson appliqua la méthode de Newton à des problèmes d'optimisation. Arthur Cayley (1821-1895) fut le premier à noter la difficulté de généraliser la méthode de Newton aux variables complexes en 1879[2], par exemple aux polynomes de degré supérieur à 3.
Interprétation et construction formelle
On va donc chercher à construire une bonne approximation d'un zéro de la fonction d'une variable réelle f(x). Pour cela, partant d'un point x0 que l'on choisit de préférence proche du zéro à trouver (en faisant des estimations grossières par exemple), on approxime la fonction au premier ordre, autrement dit, on la considère à peu près égale à sa tangente en ce point :
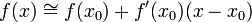 .
.
Partant de là, pour trouver un zéro de cette fonction approximante, il suffit de calculer l'intersection de la droite tangente avec l'axe des abscisses, c'est-à-dire résoudre l'équation affine :
- 0 = f(x0) + f'(x0)(x − x0).
On obtient alors un point x1 qui en général a de bonnes chances d'être plus proche du vrai zéro de f que le point x0 précédent. Par cette opération, on peut donc espérer améliorer l'approximation par itérations successives (voir illustration) : on approxime à nouveau la fonction par sa tangente en x1 pour obtenir un nouveau point x2, etc.
 Illustration de la méthode de Newton
Illustration de la méthode de Newton
Cette méthode requiert que la fonction possède une tangente en chacun des points de la suite que l'on construit par itération, par exemple il suffit que f soit dérivable.
Formellement, on part d'un point x0 appartenant à l'ensemble de définition de la fonction et on construit par récurrence la suite :
 où f' désigne la dérivée de la fonction f. Le point xn + 1 est bien la solution de l'équation affine f(xn) + f'(xn)(x − xn) = 0.
où f' désigne la dérivée de la fonction f. Le point xn + 1 est bien la solution de l'équation affine f(xn) + f'(xn)(x − xn) = 0.Il se peut que la récurrence doivent se terminer, si à l'étape n, xn n'appartient pas au domaine de définition ou si la dérivée f'(xn) est nulle, dans ce cas, la méthode a échoué.
Si le zéro inconnu α est isolé, alors il existe un voisinage de α tel que pour toutes les valeurs de départ x0 dans ce voisinage, la suite (xn) va converger vers α. De plus, si f'(α) est non nul, alors la convergence est quadratique, ce qui signifie intuitivement que le nombre de chiffres corrects est approximativement doublé à chaque étape.
Bien que la méthode soit très efficace, certains aspects pratiques doivent être pris en compte. Avant tout, la méthode de Newton nécessite que la dérivée soit effectivement calculée. Dans les cas où la dérivée est seulement estimée en prenant la pente entre deux points de la fonction, la méthode prend le nom de méthode de la sécante, moins efficace (d'ordre 1,618 qui est le nombre d'or) et inférieure à d'autres algorithmes. Par ailleurs, si la valeur de départ est trop éloignée du vrai zéro, la méthode de Newton peut entrer en boucle infinie sans produire d'approximation améliorée. À cause de cela, toute mise en œuvre de la méthode de Newton doit inclure un code de contrôle du nombre d'itérations.
Exemple
Pour illustrer la méthode, recherchons le nombre positif x vérifiant cos(x) = x3. Reformulons la question pour introduire une fonction devant s'annuler : on recherche le zéro positif (la racine) de f(x) = cos(x) − x3. La dérivation donne f'(x) = − sin(x) − 3x2.
Comme
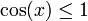 pour tout x et x3 > 1 pour x > 1, nous savons que notre zéro se situe entre 0 et 1. Nous essayons une valeur de départ de x0 = 0,5.
pour tout x et x3 > 1 pour x > 1, nous savons que notre zéro se situe entre 0 et 1. Nous essayons une valeur de départ de x0 = 0,5.Les 7 premiers chiffres de cette valeur coincident avec les 7 premiers chiffres du vrai zéro.
Convergence
La vitesse de convergence d'une suite xn obtenue par la méthode de Newton peut être obtenue comme application de la formule de Taylor. Il s'agit d'évaluer une majoration de log | xn − a | .
f est une fonction continument différentiable deux fois définie au voisinage de a. On suppose que a se trouve être un zéro de f qu'on essaie d'approximer par la méthode de Newton. On fait l'hypothèse que a est un zéro d'ordre 1, autrement dit que f'(a) est non nul. La formule de Taylor s'écrit :
 , avec ξ entre x et a.
, avec ξ entre x et a.Partant de l'approximation x, la méthode de Newton fournit au bout d'une itération :
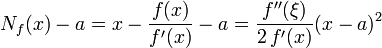 .
.Pour un intervalle compact I contenant x et a et inclus dans le domaine de définition de f, on pose :
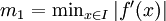 ainsi que
ainsi que 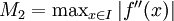 . Alors, pour tout
. Alors, pour tout 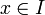 :
: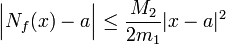 .
.Par récurrence immédiate, il vient :
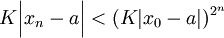
où
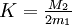 . En passant au logarithme :
. En passant au logarithme :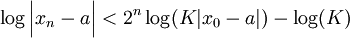
La convergence de xn vers a est donc quadratique.
Exemple de non convergence
Convergence quadratique locale
Critère d'arrêt
Des critères d'arrêt possibles, déterminés relativement à une grandeur numériquement négligeable, sont :
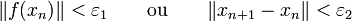
où
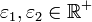 representent des erreurs d'approximations caractérisant la qualité de la solution numérique.
representent des erreurs d'approximations caractérisant la qualité de la solution numérique.Dans tous les cas, il se peut que le critère d'arrêt soit vérifié en des points ne correspondant pas à des solutions de l'équation à résoudre.
D'autres exemples d'application
Calcul de la racine carrée
Un cas particulier de la méthode de Newton est l'algorithme de Babylone, aussi connu sous le nom de méthode de Héron : il s'agit de l'appliquer à la résolution de
- f(x) = x2 − a.
On obtient alors, en utilisant la formule de la dérivée f'(x) = 2x, une méthode d'approximation de la solution
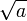 donnée par la formule itérative suivante :
donnée par la formule itérative suivante : .
.
Cette méthode converge pout tout
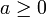 et tout point de départ
et tout point de départ 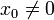 .
.Intersection des graphes de deux fonctions
De la même façon, on peut déterminer l'intersection des graphes de deux fonctions réelles dérivables f(x) et g(x), c'est à dire l'ensemble de points x où on a f(x) = g(x), en appliquant la méthode de Newton à la fonction
- f(x) − g(x).
Pour les fonctions complexes
 La méthode de Newton appliquée au polynôme z3 − 1 à variable complexe z converge à partir de tous les points du plan (des nombres complexes) colorés en rouge, vert ou bleu vers l'une des trois racines de ce polynôme, chacune des couleurs correspondant à une racine différente. Les points restants, se trouvant sur la structure plus claire - appelée fractale de Newton - sont les points de départ pour lesquels la méthode ne converge pas.
La méthode de Newton appliquée au polynôme z3 − 1 à variable complexe z converge à partir de tous les points du plan (des nombres complexes) colorés en rouge, vert ou bleu vers l'une des trois racines de ce polynôme, chacune des couleurs correspondant à une racine différente. Les points restants, se trouvant sur la structure plus claire - appelée fractale de Newton - sont les points de départ pour lesquels la méthode ne converge pas.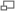
La méthode peut aussi être appliquée pour trouver des zéros de fonctions complexes . Dans ce cadre, on connait bien les comportements que peuvent avoir la suite des itérés de Newton . On peut citer :
- convergence vers un zéro,
- convergence vers l'infini,
- la suite admet un cycle limite autrement dit, la suite peut être découpée en p sous-suites disjointes de la forme
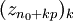 qui chacune convergent vers des points distincts (qui ne sont pas des zéros de f) formant un cycle périodique pour la fonction
qui chacune convergent vers des points distincts (qui ne sont pas des zéros de f) formant un cycle périodique pour la fonction 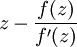 ,
, - la suite se rapproche de l'ensemble des zéros de la fonction sans qu'il n'y ait toutefois de cycle limite, et à chaque étape de l'itération, on se retrouve proche d'un zéro différent des précédents,
- la suite a un comportement chaotique, etc.
Article détaillé : Fractale de Newton.L'ensemble des points à partir desquels peut être obtenue une suite qui converge vers un zéro fixé s'appelle le bassin d'attraction de ce zéro. Pour beaucoup de fonctions complexes, le bassin d'attraction est une fractale.
L'étude de la méthode de Newton pour les polynômes à variables complexes trouve naturellement sa place dans l'étude dynamique des fractions rationnelles et a été une des motivations récentes de l'étude de la dynamique holomorphe.
Généralisations/variantes
Méthode de Newton approchée
Systèmes d'équations à plusieurs variables
On peut aussi vouloir utiliser la méthode de Newton pour résoudre des systèmes de k équations (non nécessairement linéaires), ce qui revient à trouver les zéros de fonctions continûment dérivables F de
 dans
dans  . Dans la formulation donnée ci-dessus, il faut multiplier par l'inverse de la matrice jacobienne F'(xn) au lieu de diviser par f'(xn). Plutôt que de calculer maintenant l'inverse de la matrice, on peut économiser du temps en résolvant le système d'équations linéaires
. Dans la formulation donnée ci-dessus, il faut multiplier par l'inverse de la matrice jacobienne F'(xn) au lieu de diviser par f'(xn). Plutôt que de calculer maintenant l'inverse de la matrice, on peut économiser du temps en résolvant le système d'équations linéaires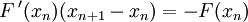
pour l'inconnue xn + 1 − xn. Encore une fois, cette méthode ne fonctionne que pour une valeur initiale x0 suffisamment proche du vrai zéro. Ainsi, on peut commencer par localiser une région favorable par une méthode grossière, puis appliquer la méthode de Newton pour peaufiner la précision.
Références
- ↑ Joseph Louis Lagrange et Louis Poinsot, Traité de la résolution des équations numériques de tous les degrés
- ↑ Arthur Cayley, The Newton-Fourier imaginary problem, 1789.
Voir aussi
Articles connexes
- Dynamique holomorphe
- Méthode de la sécante
- Méthode de la fausse position (ou méthode regula falsi)
- Méthode de Quasi-Newton
- Méthode de Müller
Liens externes
- Méthode de Newton sur maTh-linux.com.
- Portail des mathématiques
Catégories : Algorithme de recherche d'un zéro d'une fonction | Algorithme d'optimisation | Analyse numérique | Isaac Newton
Wikimedia Foundation. 2010.



