- Espace Polonais
-
Espace polonais
Un espace métrisable à base dénombrable (ou séparable, cela revient au même pour un espace métrisable) est un espace polonais si sa topologie peut être définie par une distance qui en fait un espace complet. Tout espace compact métrisable, tout sous-espace fermé ou ouvert d'un espace polonais, tout produit dénombrable d'espaces polonais, tout espace de Banach séparable est un espace polonais.
Cette terminologie a été introduite par le groupe Nicolas Bourbaki, dans son volume sur la topologie générale. C'est en fait Roger Godement, qui fut membre du groupe, qui en est a l'origine à la suite de sa proposition en 1949. De son propre aveu c'était, à la fois, humoristique et un hommage aux travaux des mathématiciens polonais dans le domaine de la topologie[1].
Exemples
- Ainsi tous les espaces usuels de l'analyse ou de l'analyse fonctionnelle sont polonais.
- Tout espace localement compact à base dénombrable est polonais (c'est un ouvert dans son compactifié d'Alexandrov).
- Mais il existe de nombreux espaces polonais intéressants dans lesquels tout compact est d'intérieur vide, par exemple les espaces de Banach séparables de dimension infinie (à cause du théorème de Riesz)
- ou encore l'espace polonais fondamental NN (appelé souvent l'espace de Baire, d'où ambiguïté avec espace de Baire) qui, à un homéomorphisme près, est le seul espace polonais totalement discontinu dans lequel tout compact est d'intérieur vide.
- Noter que ]0,1[ est un espace polonais, d'ailleurs homéomorphe à R, mais n'est pas complet pour la distance usuelle.
Propriétés
- De manière générale, un sous-espace d'un espace polonais est lui-même polonais ssi il est intersection d'une suite d'ouverts de l'espace (ce type de partie a un petit nom : on dit que c'est un Gδ ; voir classe de Baire). Ainsi les espaces polonais sont identifiables aux Gδ du cube de Hilbert.
- Les espaces polonais sont des espaces de Baire. Autrement dit, dans un espace polonais le complémentaire d'une partie maigre contient un Gδ dense.
- En particulier, si on ôte d'un espace polonais P sans points isolés un ensemble dénombrable D, il reste un sous-espace dense polonais J dont tout compact est d'intérieur vide ; si P est un intervalle de R et D l'ensemble des rationnels contenus dans P, ce qui reste est de plus totalement discontinu et donc homéomorphe à NN (appelé du coup souvent espace des irrationnels ; pour P=]0,1[, la décomposition en fraction continu(é)e donne un homéomorphisme entre J et NN).
- Toute mesure μ (bornée ou σ-finie) sur la tribu borélienne d'un espace polonais est intérieurement régulière relativement aux compacts. Autrement dit, pour tout borélien B on a
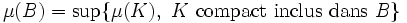 . Par conséquent, tout borélien est la réunion d'une réunion dénombrable de compacts (petit nom : Kσ) et d'un ensemble μ-négligeable.
. Par conséquent, tout borélien est la réunion d'une réunion dénombrable de compacts (petit nom : Kσ) et d'un ensemble μ-négligeable. - De ce qui précède on déduit que [0,1] est la réunion d'un Kσ maigre et d'un Gδ négligeable pour la mesure de Lebesgue. C'est une espèce de paradoxe, les ensembles maigres dans un espace de Baire étant « négligeables » du point de vue topologique.
Références
- ↑ R. Godement, Analyse mathématique IV, Springer, 2003, 599 p. (ISBN 3540438416) (Chapitre XI, §4, no 11, p. 67, note de bas de page no 30)
- Portail des mathématiques
Catégories : Topologie générale | Espace métrique
Wikimedia Foundation. 2010.
