- Espace Séparable
-
Espace séparable
En mathématiques, et plus précisément en topologie, un espace séparable est un espace topologique contenant un sous-ensemble dénombrable et dense, c'est-à-dire si l'on peut trouver un ensemble dénombrable de points dont l'adhérence est égale à l'espace topologique tout entier.
Sommaire
Lien avec les espaces à base dénombrable
Article détaillé : espace à base dénombrable.Tout espace métrisable séparable est un espace à base dénombrable et a donc au plus la puissance du continu. Sont de ce type la plupart des espaces usuels. Être à base dénombrable est une propriété beaucoup plus forte, et bien plus intéressante, qu'être séparable.
L'hypothèse de séparabilité se retrouve abondamment dans les résultats d'analyse fonctionnelle.
Un sous-espace d'un espace séparable n'est pas en général séparable. Par contre, un sous-espace d'un espace à base dénombrable est encore à base dénombrable. A fortiori, par ce qui précède, un sous-espace d'un espace métrisable séparable est encore métrisable séparable. Mais il est possible de donner une démonstration directe de cette seconde assertion sans utiliser l'équivalence entre métrisable séparable et à base dénombrable.
Soit X est un espace métrique séparable, et soit A est un sous-espace de X. On va construire une suite dense dans A. Choisissons
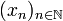 une suite dense dans X, et supposons que la topologie de X soit définie par une distance d. Pour tous entiers n et m (avec m non nul), fixons, s'il en existe, un point an,m de A vérifiant
une suite dense dans X, et supposons que la topologie de X soit définie par une distance d. Pour tous entiers n et m (avec m non nul), fixons, s'il en existe, un point an,m de A vérifiant 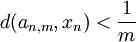 . Soit a un point de A, et soit ε un nombre de l'intervalle ]0,1] . Par définition de la suite
. Soit a un point de A, et soit ε un nombre de l'intervalle ]0,1] . Par définition de la suite 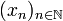 , il existe un entier n suffisamment grand pour lequel on a
, il existe un entier n suffisamment grand pour lequel on a 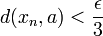 . L'intervalle
. L'intervalle ![\left]\frac 3 {2\epsilon},\frac 3 \epsilon\right[](/pictures/frwiki/55/73eccb145968736c5cbc67c33a2f44ca.png) , de longueur supérieure à
, de longueur supérieure à  , contient au moins un nombre entier. Soit m un entier de
, contient au moins un nombre entier. Soit m un entier de ![\left]\frac 3 {2\epsilon},\frac 3 \epsilon\right[](/pictures/frwiki/55/73eccb145968736c5cbc67c33a2f44ca.png) , on a
, on a ![\frac 1 m \in \left]\frac \epsilon 3,\frac {2\epsilon} 3\right[](/pictures/frwiki/100/daa7299baa984de4bfc3db1d1aeb9f8b.png) . On a
. On a 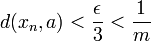 . L'ensemble
. L'ensemble 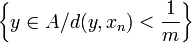 est non vide (puisqu'il contient le point a), et contient donc bien un point an,m . Et on a alors :
est non vide (puisqu'il contient le point a), et contient donc bien un point an,m . Et on a alors : 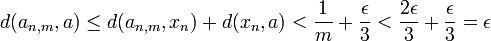 .
.La suite dénombrable (an,m) est donc bien dense dans A.
Exemples
L'ensemble
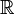 des nombres réels
des nombres réelsL'ensemble
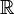 des nombres réels, muni de sa topologie usuelle, est séparable car
des nombres réels, muni de sa topologie usuelle, est séparable car 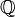 y est dense et de cardinal dénombrable.
y est dense et de cardinal dénombrable.Espace métrique précompact
Tout espace métrique précompact est séparable.
Il existe de très gros espaces compacts non métrisables mais néanmoins séparables ; c'est le cas du compactifié de Stone-Cech de N qui a même puissance que l'ensemble des parties de R.
Espaces de Lebesgue
Pour
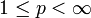 , l'espace
, l'espace 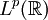 des fonctions dont la puissance p est intégrable, est séparable. Par contre, l'espace
des fonctions dont la puissance p est intégrable, est séparable. Par contre, l'espace 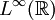 des fonctions essentiellement bornées ne l'est pas.
des fonctions essentiellement bornées ne l'est pas.- Portail des mathématiques
Catégorie : Topologie générale
Wikimedia Foundation. 2010.
