- Loi Forte Des Grands Nombres
-
Loi forte des grands nombres
La loi forte des grands nombres est un énoncé mathématique énonçant la moyenne d'une suite de variables aléatoires converge presque sûrement vers la même constante que l'espérance de la moyenne, sous certaines conditions (sur la dépendance, sur l'homogénéité et sur les moments).
Énoncé général
Le principe de la loi forte des grands nombres est que sous certaines conditions (sur la dépendance, sur l'homogénéité et sur les moments) la moyenne d'une suite de variables aléatoires {Xn} converge presque sûrement vers la même limite (constante) que l'espérance de la moyenne. En particulier, l'adjectif "fort" fait référence à la nature de la convergence établie par ce théorème : il est réservée à un résultat de convergence presque sûre. Par opposition, la loi faible des grands nombres, établie par Bernoulli, est un résultat de convergence en probabilité, seulement. Soit:
Principe général —
![\bar X_n -\bar\mu_n \xrightarrow{p.s.} 0\qquad \qquad \text{ avec } \bar X_n\equiv n^{-1}\sum_{i=1}^n X_i\text{ et } \bar \mu_n\equiv \operatorname{E}\left[\bar X_n\right]](/pictures/frwiki/101/e54b9fc0d3aaadecec81b09b9ac3026b.png)
Il existe différents théorèmes selon le type d'hypothèses faites sur la suite {Xn}[1] :
- observations indépendantes et identiquement distribuées,
- observations indépendantes et non-identiquement distribuées,
- observations dépendantes et identiquement distribuées.
Observations indépendantes et identiquement distribuées
Loi forte des grands nombres (Kolmogorov, 1929) — Si
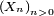 est une suite de v.a. i.i.d., on a équivalence entre:
est une suite de v.a. i.i.d., on a équivalence entre:-
- (i)
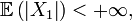
- (i)
-
- (ii) la suite
 converge presque sûrement.
converge presque sûrement.
- (ii) la suite
- De plus, si l'une de ces deux conditions équivalentes est remplie, alors la suite
 converge presque sûrement vers la constante
converge presque sûrement vers la constante 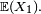
C'est la première loi forte à avoir été démontrée avec des hypothèses optimales[2]. Pour la démontrer, il fallait définir rigoureusement le concept de convergence presque sûre, ce qui a amené Kolmogorov à considérer les probabilités comme une branche de la théorie de la mesure: saut conceptuel dont Kolmogorov prouvait ainsi l'efficacité. La théorie moderne des probabilités s'est construite à partir du travail fondateur de Kolmogorov sur la loi forte des grands nombres. La loi forte des grands nombres est aussi un ingrédient important dans la démonstration d'autres lois fortes des grands nombres, comme la LFGN pour les processus de renouvellement, ou la LFGN pour les chaînes de Markov. C'est de ce théorème qu'on parle lorsqu'on dit "la loi forte des grands nombres", les autres théorèmes n'étant que des lois fortes des grands nombres. Ce théorème est aussi intéressant parce qu'il aboutit à une conclusion plus forte : il établit l'équivalence entre l'intégrabilité de la suite et sa convergence, alors que les autres théorèmes fournissent seulement des implications, sans leurs réciproques.
Observations indépendantes et non-identiquement distribuées
Théorème de Markov — Soit {Xn} une suite de variables aléatoires indépendantes d'espérance finie
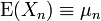 . S'il existe δ > 0 tel que
. S'il existe δ > 0 tel que 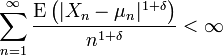 alors
alors 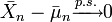
Pour pouvoir relacher l'hypothèse d'équidistribution, on est amené à faire une hypothèse plus forte sur l'intégrabilité.
Observations dépendantes et identiquement distribuées
Théorème ergodique — Soit {Xt} une suite de variables aléatoires stationnaire ergodique avec
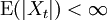 et d'espérance identique finie
et d'espérance identique finie 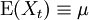 Alors
Alors 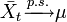
Loi forte des grands nombres de Kolmogorov
La moyenne empirique d’une suite de variables aléatoires indépendantes, identiquement distribuées, et intégrables, converge presque sûrement vers leur moyenne mathématique (ou espérance).
Autres formulations
On note souvent :
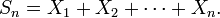
Ainsi l'énoncé devient
Théorème — Pour une suite
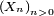 de v.a. i.i.d., on a :
de v.a. i.i.d., on a :![\ \scriptstyle \left\{\text{p.s. }\tfrac{S_{n}(\omega)}{n}\text{ est une suite convergente}\right\}\Leftrightarrow\left\{\mathbb{E}\left[\left|X_{1}\right|\right]<+\infty\right\}.](/pictures/frwiki/99/c100af4cd07cc455f7258296f0303814.png)
De plus, si l'une de ces deux conditions équivalentes est remplie, on a:
![\ \scriptstyle \mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\tfrac{S_{n}(\omega)}n=\mathbb{E}\left[X_{1}\right]\right.\right)
=
1.](/pictures/frwiki/99/cc3281f48e6983c95a0e70d1f500830c.png)
Énoncé usuel de la loi forte
L'énoncé ci-dessous est la forme habituelle de la loi forte des grands nombres, et est une conséquence directe (une forme affaiblie) du Théorème donné plus haut :
Théorème — Soit une suite
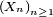 de variables aléatoires indépendantes et de même loi, intégrables. Alors
de variables aléatoires indépendantes et de même loi, intégrables. Alors![\ \scriptstyle \mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\tfrac{S_{n}(\omega)}n=\mathbb{E}\left[X_{1}\right]\right.\right)
=
1.](/pictures/frwiki/99/cc3281f48e6983c95a0e70d1f500830c.png)
Remarques
- En statistiques,
 ou bien
ou bien 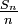 est appelée moyenne empirique des
est appelée moyenne empirique des 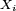 , et est souvent notée
, et est souvent notée 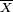 .
. - On peut formuler l'hypothèse
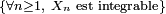 , sous différentes formes, e.g.
, sous différentes formes, e.g.
-
![\ \scriptstyle \left\{\forall n\ge1,\ \mathbb{E}\left[\left|X_{n}\right|\right]<+\infty\right\}\](/pictures/frwiki/53/5abe38452309b13d48716f3d51b83c00.png) ,
, ,
,
- ou bien encore, puisque les
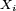 ont toutes même loi,
ont toutes même loi,
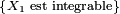 ,
,![\ \scriptstyle \left\{\mathbb{E}\left[\left|X_{1}\right|\right]<+\infty\right\}\](/pictures/frwiki/54/6d16a7525f6c724e82e2b2699d33f239.png) ,
,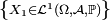 .
.
Démonstration de la loi forte de Kolmogorov
1ère étape de la démonstration : troncature
On suppose tout d'abord que les variables
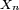 sont centrées. On n'abandonnera cette hypothèse qu'à la toute dernière étape de la démonstration. On pose
sont centrées. On n'abandonnera cette hypothèse qu'à la toute dernière étape de la démonstration. On pose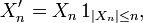
et
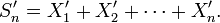
Dans cette section on démontre que
Proposition 1. — Soit une suite
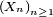 de variables aléatoires indépendantes et de même loi, intégrables. Alors (la loi forte des grands nombres)
de variables aléatoires indépendantes et de même loi, intégrables. Alors (la loi forte des grands nombres)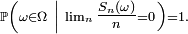
- est équivalente à
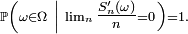 Démonstration
DémonstrationPosons

Alors
![\begin{align}
\sum_{n\ge1}\,\mathbb{P}\left(A_{n}\right)
&=
\sum_{n\ge1}\,\mathbb{P}\left(X_{n}\neq X^{\prime}_{n}\right)
\\
&=
\sum_{n\ge1}\,\mathbb{P}\left(\left|X_{n}\right|>n\right)
\\
&=
\sum_{n\ge1}\,\mathbb{P}\left(\left|X_{1}\right|>n\right)
\\
&=
\sum_{n\ge1}\,\mathbb{E}\left[1_{\left|X_{1}\right|>n}\right]
\\
&=
\mathbb{E}\left[\sum_{n\ge1}\,1_{\left|X_{1}\right|>n}\right],
\end{align}](/pictures/frwiki/100/df999a7cba14b4109809bf8c5eb9761a.png)
la 3ème égalité car
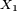 et
et 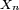 ont même loi, la dernière égalité en vertu du Théorème de convergence monotone pour les séries à termes positifs. Notons que la fonction
ont même loi, la dernière égalité en vertu du Théorème de convergence monotone pour les séries à termes positifs. Notons que la fonction 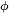 définie pour
définie pour 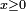 par
par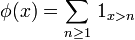
satisfait, pour
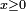 ,
,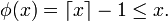
Ainsi
![\begin{align}
\sum_{n\ge1}\,\mathbb{P}\left(A_{n}\right)
&=
\mathbb{E}\left[\sum_{n\ge1}\,1_{\left|X_{1}\right|>n}\right]
\\
&=
\mathbb{E}\left[\phi\left(\left|X_{1}\right|\right)\right]
\\
&\le
\mathbb{E}\left[\left|X_{1}\right|\right]<+\infty.
\end{align}](/pictures/frwiki/48/01b99d00ef0cf491e0a5d2a2b18455ef.png)
En vertu du lemme de Borel-Cantelli, il suit que
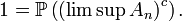
On note

et on remarque que si
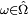 , la série
, la série
est une série convergente, puisque, en dehors d'un nombre fini d'entre eux, tous ses termes sont nuls. Ainsi la suite des sommes partielles,
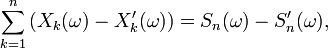
est une suite convergente, donc bornée, ce qui entraîne que

Autrement dit, en vertu de la première partie de cette démonstration,
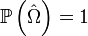
Les quelques lignes qui précèdent montrent que
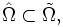
il suit donc que

Par ailleurs, il est clair que
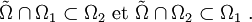
On a donc bien
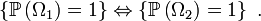
Dans les sections suivantes on va donc démontrer que

L'idée est que plus les variables concernées sont intégrables, i.e. plus la queue de distribution
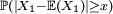 décroît rapidement, plus il est facile de démontrer la loi forte des grands nombres à l'aide du lemme de Borel-Cantelli. Ainsi il est facile de démontrer une forme affaiblie de la loi forte des grands nombres, par exemple sous l'hypothèse que les variables
décroît rapidement, plus il est facile de démontrer la loi forte des grands nombres à l'aide du lemme de Borel-Cantelli. Ainsi il est facile de démontrer une forme affaiblie de la loi forte des grands nombres, par exemple sous l'hypothèse que les variables 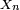 sont i.i.d. bornées, auquel cas
sont i.i.d. bornées, auquel cas 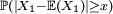 est nulle pour
est nulle pour  assez grand, ou bien sous l'hypothèse, moins brutale, que les variables
assez grand, ou bien sous l'hypothèse, moins brutale, que les variables 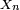 sont i.i.d. et possèdent un moment d'ordre 4, auquel cas
sont i.i.d. et possèdent un moment d'ordre 4, auquel cas 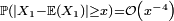 . Ici, en tronquant les
. Ici, en tronquant les 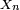 , Kolmogorov s'est ramené à des variables
, Kolmogorov s'est ramené à des variables  bornées et indépendantes, mais qui n'ont pas même loi.
bornées et indépendantes, mais qui n'ont pas même loi.2ème étape de la démonstration : recentrage
Les
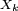 ont beau être centrées, cela n'entraîne pas que les
ont beau être centrées, cela n'entraîne pas que les 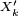 soient centrées, sauf si on suppose, par exemple, que les
soient centrées, sauf si on suppose, par exemple, que les 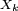 sont symétriques, i.e. sauf si
sont symétriques, i.e. sauf si 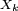 a même loi que
a même loi que 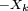 . Par exemple, si
. Par exemple, si 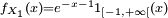 , alors, dès que
, alors, dès que 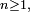
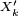 n'est pas centrée. Il est commode, pour la suite, de centrer les
n'est pas centrée. Il est commode, pour la suite, de centrer les 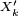 : on pose
: on pose![Z_{k}= X^{\prime}_{k}-\mathbb{E}\left[X^{\prime}_{k}\right],](/pictures/frwiki/54/6da0eb2fcc2e47186c6eb9c2d73995b5.png)
et
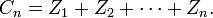
Alors
Proposition 2. — Soit une suite
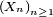 de variables aléatoires indépendantes et de même loi, intégrables. Alors
de variables aléatoires indépendantes et de même loi, intégrables. Alors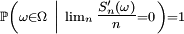
- est équivalent à
 Démonstration
DémonstrationUn calcul simple donne que
![\begin{align}
\frac{S^{\prime}_{n}(\omega)}n-\frac{C_{n}(\omega)}n
&=
\frac{\mathbb{E}\left[X^{\prime}_{1}\right]+\mathbb{E}\left[X^{\prime}_{2}\right]+\dots+\mathbb{E}\left[X^{\prime}_{n}\right]}n,
\end{align}](/pictures/frwiki/53/502816f86c3674f26453985120ca1a65.png)
la différence ne dépendant pas de
 (n'étant pas aléatoire). Par ailleurs
(n'étant pas aléatoire). Par ailleurs![\lim_{n}\mathbb{E}\left[X^{\prime}_{n}\right]=\lim_{n}\mathbb{E}\left[X_{n}1_{\left|X_{n}\right|\le n}\right]=\lim_{n}\mathbb{E}\left[X_{1}1_{\left|X_{1}\right|\le n}\right]=0.](/pictures/frwiki/52/4e5ec7391380b46a48a08fd078cc35a0.png)
En effet
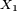 et
et 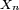 ont même loi, et, d'autre part, pour tout
ont même loi, et, d'autre part, pour tout 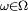 ,
,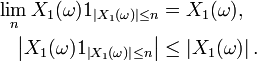
On peut donc appliquer le Théorème de convergence dominée de Lebesgue, et obtenir
![\lim_{n}\mathbb{E}\left[X^{\prime}_{n}\right]=\lim_{n}\mathbb{E}\left[X_{1}1_{\left|X_{1}\right|\le n}\right]=\mathbb{E}\left[\lim_{n}\,X_{1}1_{\left|X_{1}\right|\le n}\right]=\mathbb{E}\left[X_{1}\right]=0.](/pictures/frwiki/100/dc1ccbc7042076ad9db649663943ccd1.png)
Finalement, on sait, en vertu du lemme de Cesàro, que la convergence d'une suite (
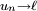 ) entraîne sa convergence en moyenne de Cesàro (
) entraîne sa convergence en moyenne de Cesàro (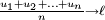 ), donc, pour tout
), donc, pour tout 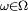 ,
,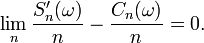
La Proposition 2 est donc démontrée.
3ème étape : Inégalité de Kolmogorov
C'est l'étape où Kolmogorov utilise l'hypothèse d'indépendance (et, sans le dire, la notion de temps d'arrêt). Par contre, l'Inégalité de Kolmogorov ne requiert pas des variables de même loi.
Inégalité de Kolmogorov. — Soit une suite
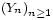 de v.a.r. indépendantes et centrées. Posons
de v.a.r. indépendantes et centrées. Posons
Alors, pour tout
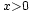 ,
,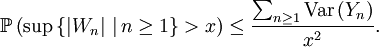 Démonstration
DémonstrationSi
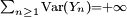 , l'inégalité est vérifiée. Dans la suite, on suppose que
, l'inégalité est vérifiée. Dans la suite, on suppose que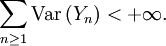
On pose

On remarque alors que, pour
 ,
,
En effet
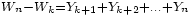 , alors que
, alors que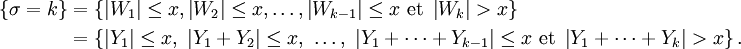
Ainsi pour deux boréliens quelconques
 et
et 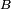 , les deux évènements
, les deux évènements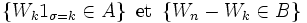
appartiennent aux tribus
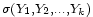 et
et 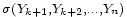 , respectivement. Ils sont donc indépendants en vertu du lemme de regroupement, ce qui implique bien
, respectivement. Ils sont donc indépendants en vertu du lemme de regroupement, ce qui implique bien 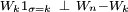 . On a
. On a![\begin{align}
\sum_{k=1}^n\,\text{Var}\left(Y_{k}\right)
&=
\text{Var}\left(W_{n}\right)\ =\ \mathbb{E}\left[W_{n}^2\right]
\\
&\ge
\mathbb{E}\left[W_{n}^21_{\sigma<+\infty}\right]
\\
&=
\sum_{k\ge1}\ \mathbb{E}\left[W_{n}^2\ 1_{\sigma=k}\right]
\\
&\ge
\sum_{k=1}^n\ \mathbb{E}\left[W_{n}^21_{\sigma=k}\right]
\\
&=
\sum_{k=1}^n\ \mathbb{E}\left[\left(W_{n}-W_{k}+W_{k}\right)^21_{\sigma=k}\right]
\\
&\ge
\sum_{k=1}^n\ \mathbb{E}\left[W_{k}^21_{\sigma=k}\right]+2\mathbb{E}\left[W_{n}-W_{k}\right]\mathbb{E}\left[W_{k}1_{\sigma=k}\right]
\\
&=
\sum_{k=1}^n\ \mathbb{E}\left[W_{k}^21_{\sigma=k}\right]
\\
&\ge
\sum_{k=1}^n\ \mathbb{E}\left[x^21_{\sigma=k}\right]
\\
&=
x^2\mathbb{P}\left(\sigma\le n\right),
\end{align}](/pictures/frwiki/54/69997ff92ae4f3d4eea979688e1b482c.png)
où la troisième inégalité s'obtient en développant le carré en deux termes carrés (dont l'un est supprimé pour minorer l'expression précédente) et un double produit (de deux variables indépendantes, en vertu de
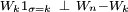 ). L'égalité suivante tient à ce que
). L'égalité suivante tient à ce que  est centrée (comme somme de v.a. centrées), et la dernière inégalité découle de la définition du temps d'arrêt
est centrée (comme somme de v.a. centrées), et la dernière inégalité découle de la définition du temps d'arrêt 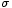 : par définition, au temps
: par définition, au temps 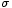 , on a
, on a 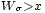 . En faisant tendre
. En faisant tendre 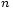 vers l'infini on obtient
vers l'infini on obtient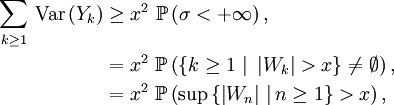
C.Q.F.D.
Voir aussi l'article en anglais sur le même sujet.
4ème étape : Convergence de séries de variables aléatoires
L'inégalité de Kolmogorov est, avec le lemme de Borel-Cantelli, l'ingrédient essentiel de la preuve de la proposition suivante :
Proposition 3. — Soit une suite
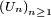 de v.a.r. indépendantes et centrées. Si
de v.a.r. indépendantes et centrées. Si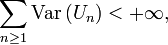
alors la suite
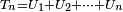 est convergente, ou bien, équivalemment, la série
est convergente, ou bien, équivalemment, la série 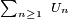 est convergente.Démonstration
est convergente.DémonstrationOn pose
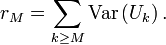
En vertu de la convergence de la série de terme général
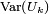 , la suite
, la suite  converge vers 0. On applique l'inégalité de Kolmogorov à la suite
converge vers 0. On applique l'inégalité de Kolmogorov à la suiteYn = UM + n. Avec les notations de l'inégalité de Kolmogorov, on a
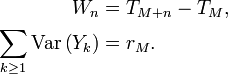
Donc l'inégalité de Kolmogorov nous donne, pour tout
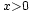 et
et 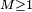 ,
,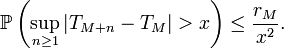
Notons que la suite de variables aléatoires
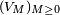 , définie par
, définie par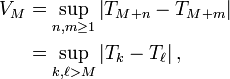
est décroissante, puisque la suite d'ensembles
 , définie par
, définie par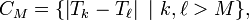
est décroissante. De plus
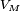 satisfait à
satisfait à
On en déduit que, pour tout
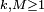 ,
,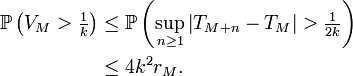
La suite
 convergeant vers 0, il suit que, pour tout
convergeant vers 0, il suit que, pour tout 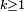 , on peut choisir
, on peut choisir 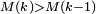 tel que
tel que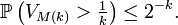
Ainsi
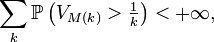
et le lemme de Borel-Cantelli entraîne que, presque sûrement, à partir d'un certain rang,
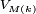 est majorée par
est majorée par  et donc que
et donc que 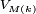 converge presque sûrement vers 0. Par ailleurs, on a vu plus haut que pour tout
converge presque sûrement vers 0. Par ailleurs, on a vu plus haut que pour tout  ,
, 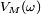 est une suite décroissante en
est une suite décroissante en 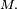 Une suite décroissante possédant une sous-suite convergente est elle-même convergente, donc
Une suite décroissante possédant une sous-suite convergente est elle-même convergente, donc 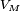 converge presque sûrement vers 0. Or
converge presque sûrement vers 0. Or
C.Q.F.D.
5ème étape : Lemme de Kronecker
Lemme de Kronecker. — Soit une suite
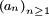 de nombres strictement positifs, décroissante vers 0. Si
de nombres strictement positifs, décroissante vers 0. Si 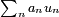 est une série convergente, alors
est une série convergente, alors Démonstration
DémonstrationLa démonstration ci-dessous vaut seulement pour
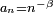 ,
, 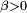 , mais la démonstration de la loi forte utilise le lemme de Kronecker pour
, mais la démonstration de la loi forte utilise le lemme de Kronecker pour 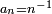 ,
, 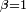 . On peut trouver une démonstration générale du Lemme de Kronecker ici. Posons
. On peut trouver une démonstration générale du Lemme de Kronecker ici. Posons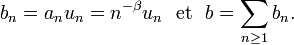
Alors

Comme la suite
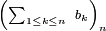 est convergente, il existe un réel
est convergente, il existe un réel 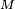 tel que
tel que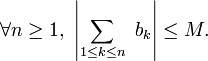
Donc la suite de fonctions
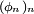 définies sur
définies sur ![\ \scriptstyle [0,1] \](/pictures/frwiki/57/911312ad6fe325a8c9894661a9f2502e.png) par
par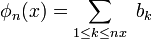
est une suite de fonctions uniformément bornées par
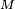 (en valeur absolue). De plus, pour tout
(en valeur absolue). De plus, pour tout ![\ \scriptstyle x\in[0,1] \](/pictures/frwiki/100/d731b25851e592b89875d870e80d17b7.png) ,
,
Ainsi le théorème de convergence dominée de Lebesgue donne
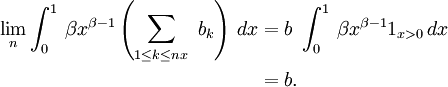
Comme on a
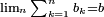 , en observant le second terme de l'identité
, en observant le second terme de l'identité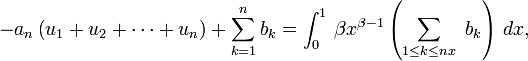
démontrée plus haut, on en déduit que

C.Q.F.D.
Cette démonstration est empruntée à Sydney Resnik, A probability path.
Pour conclure sa démonstration, Kolmogorov utilise le lemme de Kronecker avec
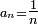 , voir section suivante.
, voir section suivante.6ème étape : Conclusion dans le cas de variables centrées
Lemme 1. — Avec les notations de l'étape "recentrage", on a
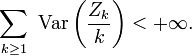 Démonstration
DémonstrationLes calculs s'arrangent mieux si on remplace
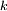 par
par 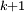 au dénominateur. Pour
au dénominateur. Pour 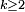 on a
on a![\text{Var}\left(\frac{Z_{k}}{k+1}\right)\
=
\ \frac{\mathbb{E}\left[X^{\prime 2}_{k}\right]}{(k+1)^2}\
-
\ \frac{\mathbb{E}\left[X^{\prime}_{k}\right]^2}{(k+1)^2}.](/pictures/frwiki/56/82e0076fc76bf5079ac035172a90f2e1.png)
Comme
![\ \scriptstyle \lim_{n} \mathbb{E}\left[X^{\prime}_{n}\right]=0 \](/pictures/frwiki/55/78b8802a904b56a14d1b8c828be8e2ec.png) ,
,![\frac{\mathbb{E}\left[X^{\prime}_{k}\right]^2}{(k+1)^2}=o\left(\frac{1}{k^2}\right),](/pictures/frwiki/52/4100b798acdbc4cd2b9a4c5f2a060e77.png)
et la convergence de la série
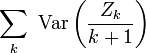
est équivalente à la convergence de la série
![\sum_{k}\ \frac{\mathbb{E}\left[X^{\prime 2}_{k}\right]}{(k+1)^2}.](/pictures/frwiki/53/59a3d7d6bcf2debe709a405a713f8b17.png)
Or
![\begin{align}
\sum_{k\ge 1}\ \frac{\mathbb{E}\left[X^{\prime 2}_{k}\right]}{(k+1)^2}
&=
\sum_{k\ge 1}\ (k+1)^{-2}\ \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|\le k}\right]
\\
&\le
\sum_{k\ge 1}\ \int_{k}^{k+1}x^{-2}\ \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|\le x}\right]\ dx
\\
&=
\int_{1}^{+\infty}x^{-2}\ \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|\le x}\right]\ dx
\\
&=
\mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|}\ \int_{1}^{+\infty}x^{-2}\ 1_{\left|X_{1}\right|\le x}\ dx\right]
\\
&\le
\mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|}\ \int_{\left|X_{1}\right|}^{+\infty}\ x^{-2}\ dx\right]
\\
&=
\mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|}\left|X_{1}\right|^{-1}\right]
\\
&=
\mathbb{E}\left[\left|X_{1}\right|\right]\ <\ +\infty,
\end{align}](/pictures/frwiki/53/51a4ba1b40c461db1563175e906fd06d.png)
par hypothèse.
Du Lemme 1 et de la Proposition 3, on déduit que, presque sûrement,
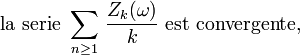
puis, grâce au lemme de Kronecker, on déduit que, presque sûrement,
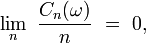
ce qui est équivalent à la loi forte des grands nombres (pour des variables centrées), comme on l'a vu aux étapes "troncature" et "recentrage".
7ème étape : décentrage
Si on ne suppose plus les
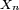 centrées, mais seulement i.i.d. et intégrables, on pose
centrées, mais seulement i.i.d. et intégrables, on pose![\hat{X}_{k}= X_{k}-\mathbb{E}\left[X_{k}\right],\ \ \hat{S}_{n}= \hat{X}_{1}+\hat{X}_{2}+\cdots+\hat{X}_{n},](/pictures/frwiki/48/0a70ae910d3dde1d6c6a09bfd2d82817.png)
et, les
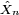 étant centrées, i.i.d. et intégrables, la conclusion des étapes précédentes est que
étant centrées, i.i.d. et intégrables, la conclusion des étapes précédentes est que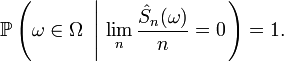
Mais
![\begin{align}
\frac{\hat{S}_{n}(\omega)}n
&=
\frac{S_{n}(\omega)-n\mathbb{E}\left[X_{1}\right]}n
\\
&=
\frac{S_{n}(\omega)}n\ -\ \mathbb{E}\left[X_{1}\right].
\end{align}](/pictures/frwiki/102/fe60cbc818cb8ade19cbae7c09762e1d.png)
Donc
![\mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\frac{\hat{S}_{n}(\omega)}n=0\right.\right)
=
\mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\frac{S_{n}(\omega)}n=\mathbb{E}\left[X_{1}\right]\right.\right)
.](/pictures/frwiki/55/790887b5427aee7f65a72c5365beaba3.png)
C.Q.F.D.
Notes et références
- ↑ Classification et notation reprise de White (1984).
- ↑ On doit à Émile Borel une version de la LFGN pour les variables de Bernoulli, dès 1909, dans l'article Les probabilités dénombrables et leurs applications arithmétiques. Rend. Circ. Math. Palermo 27, pp. 247-271.
Voir aussi
Articles connexes
- Andreï Kolmogorov
- Francesco Paolo Cantelli
- Émile Borel
- Loi des grands nombres
- Théorème de la limite centrale
- Théorème des 3 séries de Kolmogorov
Références
- (en) Halbert White, Asymptotic Theory for Econometricians, Academic Press, Orlando (ISBN 0127466509), p. 228
- Sidney I. Resnick, A Probability Path [détail des éditions]
Liens externes
- Le site officiel en l'honneur d'Andreï Kolmogorov
- Un site sur son livre fondateur de la théorie moderne des probabilités, Grundbegriffe der Wahrscheinlichkeitsrechnung, 1933
- La page de ce livre où apparait sa démonstration de la loi forte des grands nombres
- Portail des probabilités et des statistiques
Catégories : Probabilités | Théorème de mathématiques
Wikimedia Foundation. 2010.
