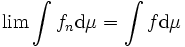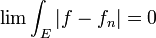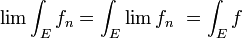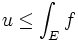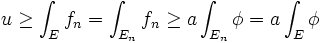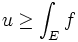- Theoreme de convergence monotone
-
Théorème de convergence monotone
En mathématiques, le Théorème de convergence monotone est l'un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée.
Ce théorème indique que la convergence simple d'une suite de fonctions mesurables positives est aussi une convergence au sens de la norme L1 si la suite est croissante.
Il permet, sous réserve de respecter les hypothèses du théorème, d'inverser les 2 symboles mathématiques
 et
et  . Comme cas particulier, il permet aussi d'inverser les deux symboles
. Comme cas particulier, il permet aussi d'inverser les deux symboles  et
et 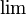 sous les mêmes hypothèses ou encore les deux symboles
sous les mêmes hypothèses ou encore les deux symboles 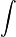 et
et  dans le cas de série.
dans le cas de série.Sommaire
Énoncé du théorème
Soit E un espace mesurable, (fn) une suite croissante de fonctions positives mesurables de E dans R qui converge simplement presque partout, alors la limite f est une fonction mesurable et :
On peut également exprimer ce résultat en disant que la suite (fn) converge vers f pour la norme L1.
Histoire
Au début du XXe siècle une nouvelle théorie de l'intégration apparaît sous la forme d'un article Sur une généralisation de l'intégrale définie, publié dans les Comptes Rendus du 29 Avril 1901. Cet article fascine rapidement la communauté mathématique. En 1906, le mathématicien italien Beppo Levi (1875-1961) démontre le théorème de la convergence monotone qui porte en conséquence parfois le nom de théorème de Beppo Levi.
Remarques
Convergence simple
Une fonction non élémentaire en mathématiques est souvent construite comme limite d'une suite et plus généralement d'une série. Ces fonctions sont par exemple obtenues par une construction de type série entière ou par les méthodes de l'analyse harmonique.
Parfois, cette série converge bien. Par bien converger, on entend la convergence au sens d'une topologie forte ou d'une bonne distance. Par exemple, la distance de la convergence uniforme qui indique qu'une section finissante de la suite se trouve dans une bande de largeur aussi petite que l'on veut.
Malheureusement une convergence forte est rare. Par exemple la suite des polynômes (xn) sur l'intervalle [0, 1] ne converge pas uniformément. Un critère de convergence peu contraignant est la convergence simple, qui indique uniquement qu'en chaque point les fonctions convergent. La régularité de la convergence n'est pas assurée. Si le critère de convergence est peu contraignant, il offre hélas des propriétés peu enrichissantes. C'est la raison pour laquelle on appelle la topologie associée la topologie faible. C'est le cas de notre exemple qui converge vers la fonction égale à 0 sur l'intervalle [0,1[ et vers 1 en 1.
Convergence presque partout
Presque partout signifie que la propriété est vraie en chaque point sauf peut-être sur un ensemble de mesure nulle. En effet, le comportement d'une fonction est invariant pour l'intégrale de Lebesgue si la fonction n'est modifiée que sur un ensemble de mesure nulle.
Convergence L1
Il existe un critère de convergence fondé sur une distance provenant directement de la mesure. Cette distance d est définie de la manière suivante, si E est un espace mesurable, f et g des fonctions définies sur E presque partout, à valeur dans les réels et mesurables alors :
d(f,g) = ∫ | f − g | E L'espace vectoriel des fonctions mesurables de E à valeur dans les réels définies presque partout muni de cette distance est noté
 . Le théorème de la convergence monotone indique que la convergence a lieu dans cet espace. Une autre manière d'énoncer ce résultat revient à dire que l'on peut intervertir les signes de limites et d'intégrale. Si l'on note
. Le théorème de la convergence monotone indique que la convergence a lieu dans cet espace. Une autre manière d'énoncer ce résultat revient à dire que l'on peut intervertir les signes de limites et d'intégrale. Si l'on note 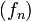 la suite de fonctions de f la limite, exprimer la convergence de la suite dans
la suite de fonctions de f la limite, exprimer la convergence de la suite dans  c'est dire que:
c'est dire que:ce qui entraîne
Intérêt du théorème
L'aspect remarquable de la théorie de Lebesgue est qu'un critère de convergence faible suffit néanmoins sous certaines hypothèses pour assurer une bonne convergence, la convergence dans L1(E). Ce résultat est donc indispensable pour l'étude d'espaces de fonctions un peu subtils comme l'espace des séries entières, des fonctions harmoniques ou des espaces de Hardy ou de Sobolev.
Théorème de convergence dominée
On utilise une forme souvent plus puissante de ce théorème : le théorème de convergence dominée. Il ne s'applique cependant pas si la suite n'est pas majorée par une fonction mesurable, ce qui est donc le cas le plus fréquent d'utilisation de la convergence monotone. Par ailleurs, on utilise habituellement le théorème de convergence monotone pour prouver le théorème de convergence dominée.
Non validité dans le cadre de la théorie de Riemann
Ce théorème serait faux avec la construction de l'intégrale de Riemann. Construisons le contre-exemple suivant: Soit (un) une suite de rationnels bijective dans l'intervalle [0,1] de Q. Définissons la suite de fonctions (fn) de [0,1] dans l'ensemble des réels positifs par :
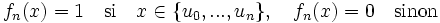 .
.
Cette suite converge simplement vers une fonction qui est nulle sur les irrationnels et constante de valeur 1 sur les rationnels. Elle ne converge pas pour l'intégrale de Riemann.
DémonstrationSoit
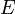 un espace mesurable et (fn) une suite croissante de fonctions positives mesurables de
un espace mesurable et (fn) une suite croissante de fonctions positives mesurables de 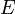 dans
dans  qui converge simplement presque partout. Notons f sa limite. Elle est mesurable car elle est égale à la fonction
qui converge simplement presque partout. Notons f sa limite. Elle est mesurable car elle est égale à la fonction 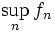 qui est mesurable (cf fonction mesurable). Définissons la suite (un) la suite de réels définie par:
qui est mesurable (cf fonction mesurable). Définissons la suite (un) la suite de réels définie par:-
un = ∫ fn E
La suite (un) est convergente au besoin vers la valeur
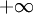 , vers une limite que nous notons u, car elle est croissante. Par construction, la fonction f majore toutes les fonctions de la suite (fn), donc:
, vers une limite que nous notons u, car elle est croissante. Par construction, la fonction f majore toutes les fonctions de la suite (fn), donc:Soit φ une fonction étagée majorée par f et a un réel strictement compris entre 0 et 1. On définit alors l'ensemble En par:
 .
.
La suite (En) est une suite d'ensembles emboîtés dont une section finissante est égale à
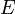 . On en déduit que si n est suffisamment grand alors:
. On en déduit que si n est suffisamment grand alors:Cette inégalité est vraie pour tout a positif plus petit que 1 elle est donc aussi vraie si a est égal à 1. Cette inégalité est vraie pour toute fonction étagée majorée par f elle est donc vraie pour f, nous avons donc:
Nous avons démontré que u est égal à l'intégrale de f sur E. CQFD
Voir aussi
Liens internes
- Mesure
- Espace mesurable
- Fonction mesurable
- Ensemble de mesure nulle
- Convergence simple
- Intégrale de Lebesgue
- Lemme de Fatou
- Théorème de convergence dominée
Liens externes
- Mathématiques pour la Licence
- Théorème de la convergence dominée de Lebesgue
- Théorème de Lebesgue dans un cas simple
- Portail des mathématiques
Catégories : Théorie de la mesure | Théorème de mathématiques
Wikimedia Foundation. 2010.