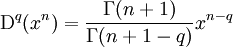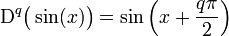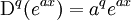- Analyse Fractionnaire
-
Analyse fractionnaire
L' analyse fractionnaire est une branche de l'analyse qui étudie la possibilité qu'un opérateur différentiel puisse être élevé à un ordre non entier.
On peut définir par ce procédé des dérivées ou des intégrales fractionnaires. Ces dérivées ou intégrations fractionnaires rentrent dans le cadre plus général des opérateurs pseudo-différentiels.
Les dérivées fractionnaires sont utilisées par exemple dans certains domaines de la physique faisant intervenir des phénomènes de diffusion comme l'électromagnétisme, l'acoustique ou la thermique, en définissant des opérateurs pseudo-différentiels diffusifs, avec conditions de bord à « géométrie fractale ».
Par exemple, on peut se demander comment interpréter convenablement
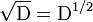
comme la racine carrée de l'opérateur de dérivation (un opérateur à moitié itéré), c'est-à-dire une expression d'un certain opérateur qui, lorsqu'elle est appliquée deux fois à une fonction aura le même effet que la dérivation. Plus généralement, on peut examiner le problème de définir
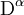
pour des valeurs réelles de α, de telle sorte que lorsque α prend une valeur entière n, on récupère la dérivation n-ième usuelle pour n > 0 ou l'intégration itérée − n fois pour n < 0. Le terme « fractionnaire » est utilisé de façon impropre : α n'est pas nécessairement un nombre rationnel. Cependant, le terme « analyse fractionnaire » est devenu traditionnel.
Sommaire
Dérivée fractionnaire
En ce qui concerne l'existence d'une telle théorie, les fondations de ce sujet ont été jetées par Liouville dans un article de 1832. La dérivée fractionnaire d'ordre a d'une fonction en un point x est désormais souvent définie à partir de la transformée de Fourier ou de la transformée de Laplace.
Un point important est que la dérivée fractionnaire d'une fonction en un point x est une propriété locale seulement lorsque l'ordre a est entier ; dans les autres cas, on ne peut plus dire que la dérivée fractionnaire d'une fonction f en x ne dépend que du voisinage de f très près de x, comme c'est le cas en ce qui concerne les ordres des dérivations entiers.
Pour illustrer ceci, introduisons l'opérateur « de translation »
 et l'opérateur identité Id. La limite, lorsque h tend vers 0, de l'opérateur
et l'opérateur identité Id. La limite, lorsque h tend vers 0, de l'opérateur
correspond bien à l'opérateur de dérivation au premier ordre.
Grâce à la formule du binôme généralisé, on peut alors élever cet opérateur à une puissance non entière. On obtient ainsi une série infinie :
![\Delta^\alpha = \frac{(T - \mathrm{\mathrm Id})^\alpha}{h^\alpha} = \frac1{h^\alpha}\left[ \mathrm{\mathrm Id} + \sum_{k=1}^\infty (-1)^k \frac{\alpha(\alpha-1)\ldots(\alpha-k+1)}{k!} T^k \right]](/pictures/frwiki/54/638edbf9d6bec2ec5748d55cb26a8082.png)
Ce résultat met bien en évidence le caractère non local de l'opération de dérivation à un ordre non entier.
Approche naturelle
Une question naturelle qui se pose est : existe-t-il un opérateur H tel que
 ?
?Il apparaît qu'il existe un tel opérateur, et en effet pour tout α > 0, il existe un opérateur P tel que :
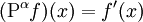 ,
,ou, pour le formuler autrement, que
 est bien défini pour toutes valeurs réelles n > 0.
est bien défini pour toutes valeurs réelles n > 0.Un résultat similaire s'applique pour l'intégration. Considérant une fonction f(x) qui est bien définie pour x > 0, nous pouvons former son intégrale définie de 0 à x :
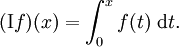
En répétant ce processus, on obtient
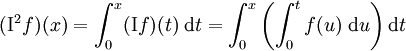 ,
,et ceci peut être répété arbitrairement.
La formule suivante, appelée formule de Cauchy,
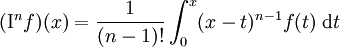
exprime par une seule intégrale la primitive nème d'une fonction f. Ceci mène tout droit à une généralisation pour tout réel α.
La fonction gamma Γ, qui étend la factorielle aux valeurs réelles, est définie de telle sorte que :
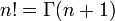 .
.En utilisant la fonction gamma pour se libérer de la nature discrète de la factorielle, nous obtenons un candidat naturel pour les applications fractionnaires de l'opérateur d'intégration :

On peut montrer que l'opérateur I est commutatif et additif :
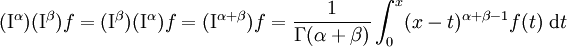
Malheureusement, le processus analogue pour l'opérateur de dérivation D est considérablement plus compliqué. En général, D n'est ni commutatif, ni additif.
Exemple : « demi-dérivée » d'une fonction simple
Considérons f(x), un monôme de la forme
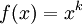 .
.La dérivée première est communément
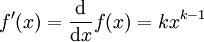 .
.Ceci mène, après a répétitions, au résultat plus général
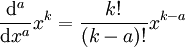 ;
;lequel, après substitution des factorielles par la fonction gamma, donne :
 .
.Ainsi, la « demi-dérivée » de f(x) = x est :
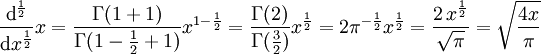 .
.Une seconde application donne :
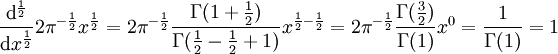 ,
,ce qui est bien le résultat attendu de :
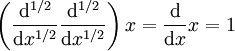
Résultats élémentaires
On peut ainsi arriver à quelques formules de base, permettant d'évaluer des dérivées « fractionnaires » dans quelques cas simples :
Voir aussi
Liens internes
Liens externes
- Stéphane Dugowson, Les différentielles métaphysiques (histoire et philosophie de la généralisation de l'ordre de dérivation), Thèse, Université Paris Nord (1994)
- Opérateurs Pseudo-Différentiels et Représentation Diffusive en Modélisation, Contrôle et Signal
- Fractional calculus sur MathWorld
- Fractional derivative sur MathWorld
- Fractional Calculus and Applied Analysis : journal de l'Institut de mathématiques de l'Académie bulgare des sciences ;
- Initialized Fractional Calculus
- Fractional Calculus Project
- Ressources sur l'analyse fractionnaire chez Igor Podlubny
- [pdf]History, Definitions, and Applications for the Engineer, par Adam Loverro
Bibliographie
- Introduction au calcul fractionnaire, by Denis Matignon, dans Lois d'échelle, fractales et ondelettes', Hermes, Paris, 2002
- Theory and Applications of Fractional Differential Equations, by Kilbas, A. A.; Srivastava, H. M.; and Trujillo, J. J. Amsterdam, Netherlands, Elsevier, Febrary 2006. ISBN 0-444-51832-0 (http://www.elsevier.com/wps/find/bookdescription.cws_home/707212/description#description)
- An Introduction to the Fractional Calculus and Fractional Differential Equations, by Kenneth S. Miller, Bertram Ross (Editor). Hardcover: 384 pages. Publisher: John Wiley & Sons; 1 edition (May 19, 1993). ISBN 0-471-58884-9
- The Fractional Calculus; Theory and Applications of Differentiation and Integration to Arbitrary Order (Mathematics in Science and Engineering, V), by Keith B. Oldham, Jerome Spanier. Hardcover. Publisher: Academic Press; (November 1974). ISBN 0-12-525550-0
- Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications., (Mathematics in Science and Engineering, vol. 198), by Igor Podlubny. Hardcover. Publisher: Academic Press; (October 1998) ISBN 0-12-558840-2
- Fractals and Fractional Calculus in Continuum Mechanics, by A. Carpinteri (Editor), F. Mainardi (Editor). Paperback: 348 pages. Publisher: Springer-Verlag Telos; (January 1998). ISBN 3-211-82913-X
- Physics of Fractal Operators, by Bruce J. West, Mauro Bologna, Paolo Grigolini. Hardcover: 368 pages. Publisher: Springer Verlag; (January 14, 2003). ISBN 0-387-95554-2
- Fractional Calculus and the Taylor-Riemann Series, Rose-Hulman Undergrad. J. Math. Vol.6(1) (2005).
- Operator of fractional derivative in the complex plane, by Petr Zavada, Commun.Math.Phys.192, pp. 261-285,1998. doi:10.1007/s002200050299 (available online or as the arXiv preprint)
- Relativistic wave equations with fractional derivatives and pseudodifferential operators, by Petr Zavada, Journal of Applied Mathematics, vol. 2, no. 4, pp. 163-197, 2002. doi:10.1155/S1110757X02110102 (available online or as the arXiv preprint)
- Portail des mathématiques
Catégorie : Analyse fonctionnelle
Wikimedia Foundation. 2010.