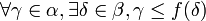- Nombre Cardinal
-
Nombre cardinal
 Pour les articles homonymes, voir Cardinal.
Pour les articles homonymes, voir Cardinal.
En mathématiques, la cardinalité est une notion de taille pour les ensembles. Les nombres cardinaux permettent donc de mesurer l'ampleur de tout ensemble, même infini, là où les entiers naturels ne comptent le nombre d'éléments que d'ensembles finis.Sommaire
Le concept
Les saisons, les points cardinaux, les fils Aymon, forment trois ensembles partageant une certaine qualité, qu'ils ne partagent pas avec l'ensemble des doigts de la main : on peut mettre en évidence cette qualité en faisant correspondre un à un les éléments respectifs de ces ensembles et dire qu'ils sont de cardinal « quatre »[1]. « Quatre » serait alors la signature de la propriété en question.
De la même façon l'ensemble des doigts de la main peut être mis en correspondance, élément par élément, avec l'ensemble des mots {« Amérique », « Afrique », « Antarctique », « Océanie », « Eurasie »} ; ces deux ensembles sont en un certain sens équivalents.
Cependant, il n' y a aucun moyen de mettre en correspondance « un à un » chaque point cardinal avec chaque doigt de la main; et donc là on n'a pas affaire à des ensembles équivalents.
Ce que l'on appelle « cardinal » sera en quelque sorte la mesure de la « puissance » d'un ensemble.
Ainsi donc les cardinaux apparaissent sous le double aspect de l' équivalence et de l' ordre : chacun d'eux est la signature d'une équivalence entre ensembles, mais entre eux ils sont ordonnés par taille.
Définitions
Le cardinal d'un ensemble est défini comme étant le nombre d'éléments de ce dernier.
Définition classique
Dans la théorie des ensembles de Zermelo-Fraenkel (ZF), l'adjonction de l'axiome du choix (donnant la théorie ZFC) permet de définir le cardinal d'un ensemble comme le plus petit nombre ordinal qui lui est équipotent. Un nombre cardinal est alors un ordinal qui n'est équipotent à aucun de ses éléments. Sans l'axiome du choix, mais avec l'axiome de fondation, on utilise la définition de Frege (ou plus précisément une amélioration technique de cette idée, due à Scott) : le cardinal de x est l'ensemble des ensembles de rang minimum équipotent à x. On sait que sans l'axiome du choix ni l'axiome de fondation, il est impossible de définir (en général) la notion de nombre cardinal.
S'il existe une injection d'un ensemble A dans un ensemble B alors il existe une injection de n'importe quel ensemble équipotent à A dans n'importe quel ensemble équipotent à B. Le théorème de Cantor-Bernstein permet de montrer que deux cardinaux sont égaux s'il existe une injection de chacun d'eux dans l'autre. Cette relation est donc une relation d'ordre (partiel) sur les cardinaux. Le fait qu'elle est totale ou linéaire équivaut à l'axiome du choix.
L'ensemble vide et les ensembles d'entiers de la forme
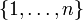 forment des ensembles de cardinaux deux à deux différents.
forment des ensembles de cardinaux deux à deux différents.
Un ensemble est dit fini s'il est équipotent à l'un de ces ensembles, infini dans le cas contraire. Tout cardinal fini est inférieur à tout cardinal infini.Sans l'axiome du choix, il peut être judicieux de se limiter aux ensembles pour lesquels un tel ordinal équipotent existe.
On note
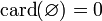 et
et 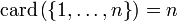 , de sorte que l'ordre sur les cardinaux prolonge l'ordre sur les entiers naturels.
, de sorte que l'ordre sur les cardinaux prolonge l'ordre sur les entiers naturels.Or l'ensemble vide n'est équipotent qu'à lui-même ; donc dans une théorie où les objets du discours sont tous des ensembles, on a nécessairement
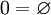 .
.La définition des autres entiers n'est pas aussi évidente, mais selon celle de Von Neumann, la plus utilisée (et qui a le mérite de se prolonger à tous les ordinaux), pour tout entier naturel
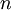 , on a
, on a 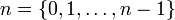 .
.Définition de Frege
La relation d'équipotence étant réflexive, symétrique et transitive sur la classe des ensembles, chaque classe d'équivalence est appelée nombre cardinal ou simplement cardinal.
Cette définition qui paraît très naturelle se présente parfois dans les exposés élémentaires de la théorie des ensembles ; cependant son usage pose des problèmes d'ordre logique, en particulier elle est incompatible avec les théories usuelles où soit on ne considère que des ensembles, soit on considère des classes propres mais qui ne peuvent être éléments d'autres classes. Ces difficultés s'apparentent au paradoxe de Russell, qui fut d'ailleurs découvert quand ce dernier adressa une lettre critique à Frege. La solution de ces problèmes, due à Dana S. Scott, consiste à utiliser l'ensemble des x de rang minimum contenu dans une telle classe, ce qui suppose l'axiome de fondation ; il ne semble pas possible de généraliser encore cette définition si l'on ne dispose pas d'un axiome de ce genre.
Propriétés générales
Si f est une fonction de A dans B, alors
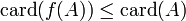 .
.Théorème fondamental
Il n'existe pas de surjection d'un ensemble E sur l'ensemble de ses parties
 . Un ensemble n'est donc jamais équipotent à l'ensemble de ses parties, bien qu'il s'injecte dedans par l'ensemble des singletons de ses éléments, ce qui permet d'écrire :
. Un ensemble n'est donc jamais équipotent à l'ensemble de ses parties, bien qu'il s'injecte dedans par l'ensemble des singletons de ses éléments, ce qui permet d'écrire : .
.
C'est le théorème de Cantor.
Ce résultat justifie le fait qu'il existe des infinis de cardinaux différents. Il donne même un procédé de construction d'une infinité d'entre eux par itération.
Les cardinaux infinis sont représentés au moyen de la lettre hébraïque aleph
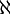 . Le plus petit cardinal infini est
. Le plus petit cardinal infini est 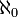 . C'est le cardinal de l'ensemble
. C'est le cardinal de l'ensemble  des entiers naturels, qui est également désigné en tant que nombre ordinal par ω. Le cardinal immédiatement supérieur est
des entiers naturels, qui est également désigné en tant que nombre ordinal par ω. Le cardinal immédiatement supérieur est 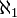 , etc. D'une manière générale, un cardinal quelconque s'écrit
, etc. D'une manière générale, un cardinal quelconque s'écrit 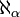 où α est un ordinal.
où α est un ordinal.Cardinal fini
Le cardinal d'un ensemble fini correspond donc simplement au nombre d'éléments qu'il contient. Par exemple, card({1,2,5}) = 3.
Toute partie d'un ensemble fini est finie.
Cardinal infini
Si A est infini alors
 est noté 2card(A) par analogie avec le cas fini.
est noté 2card(A) par analogie avec le cas fini.Exemples
- Le cardinal de l'ensemble des nombres réels est le même que celui de l'ensemble des parties de
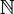 :
:
-
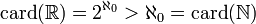 .
.
- Ce cardinal étant égal à celui de
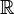 , on le note également
, on le note également  , dit cardinal du continu.
, dit cardinal du continu.
- Cependant, l'ensemble des entiers naturels et l'ensemble des rationnels sont équipotents.
-
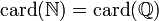 .
.
Article détaillé : Ensemble dénombrable.- De même que
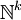 s'injecte dans
s'injecte dans  pour tout entier k,
pour tout entier k, 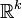 s'injecte dans
s'injecte dans 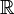 , par conséquent le cardinal de
, par conséquent le cardinal de 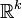 est égal à
est égal à  , cardinal de
, cardinal de 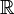 . Démonstration succincte : on montre que [0,1]2 s'injecte dans [0,1] (d'où le fait que
. Démonstration succincte : on montre que [0,1]2 s'injecte dans [0,1] (d'où le fait que 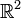 puis
puis 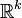 par récurrence s'injecte dans
par récurrence s'injecte dans 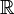 , l'existence d'une bijection provenant du théorème de Cantor-Bernstein). Pour cela, il suffit d'écrire tout élément de [0,1] comme suite de 0 et de 1 (développement binaire). L'image d'un élément de [0,1]2 est formé en intercalant successivement chaque chiffre du développement binaire du premier et second nombre. On vérifie facilement que c'est une application injective (en prenant garde toutefois aux problèmes de non unicité du développement binaire). En utilisant un raisonnement similaire, on montre que l'ensemble des suites de réels est de cardinal
, l'existence d'une bijection provenant du théorème de Cantor-Bernstein). Pour cela, il suffit d'écrire tout élément de [0,1] comme suite de 0 et de 1 (développement binaire). L'image d'un élément de [0,1]2 est formé en intercalant successivement chaque chiffre du développement binaire du premier et second nombre. On vérifie facilement que c'est une application injective (en prenant garde toutefois aux problèmes de non unicité du développement binaire). En utilisant un raisonnement similaire, on montre que l'ensemble des suites de réels est de cardinal  .
. - Le cardinal de l'ensemble des fonctions continues de
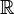 dans
dans 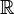 est égal à
est égal à  , cardinal de
, cardinal de 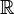 . Ceci découle de la proposition précédente, car l'ensemble des fonctions réelles continues a au plus la puissance de
. Ceci découle de la proposition précédente, car l'ensemble des fonctions réelles continues a au plus la puissance de  (et au moins celle du continu).
(et au moins celle du continu). - Le cardinal de l'ensemble des fonctions de
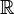 dans
dans 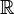 est
est 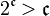 .
.
Propriétés
- Un ensemble A est infini si et seulement si
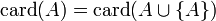 .
. - Si A est infini et si
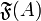 désigne l'ensemble des parties finies de A, alors
désigne l'ensemble des parties finies de A, alors  .
. - Si A est infini et B non vide, alors
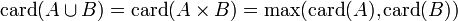 .
. - Si B est inclus dans A infini avec card(B) < card(A), alors
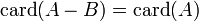 .
. - Si A est infini, alors
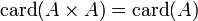
- Si A est infini et si
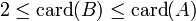 , alors
, alors 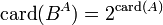 où BA désigne l'ensemble des fonctions de A dans B.
où BA désigne l'ensemble des fonctions de A dans B.
Cardinal inaccessible
L'accessibilité est la possibilité d'atteindre un ordinal ou un cardinal donné à partir des ordinaux plus petits.
Un ordinal α est dit cofinal avec un ordinal β inférieur s'il existe une application strictement croissante f de β dans α tel que α soit la limite de f au sens suivant :Par exemple,
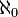 n'est cofinal avec aucun ordinal strictement plus petit, puisqu'un ordinal inférieur à
n'est cofinal avec aucun ordinal strictement plus petit, puisqu'un ordinal inférieur à 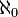 est un entier n = {0,1,...,n − 1} et qu'une application strictement croissante définie sur {0,1,...,n − 1} est bornée. Le cardinal
est un entier n = {0,1,...,n − 1} et qu'une application strictement croissante définie sur {0,1,...,n − 1} est bornée. Le cardinal 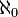 est dit alors régulier, c'est le cas de tous les cardinaux successeurs.
est dit alors régulier, c'est le cas de tous les cardinaux successeurs.Par contre, le cardinal
 est cofinal avec ω au moyen de l'application
est cofinal avec ω au moyen de l'application 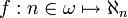 .
.
Ce cardinal est dit alors singulier.
est dit alors singulier.En notant cf(α) le plus petit ordinal pour lequel α est cofinal, on obtient
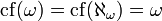 .
.Les cardinaux se classent alors comme suit :
- ceux de la forme
 , indexés par un ordinal α + 1 successeur d'un ordinal α ;
, indexés par un ordinal α + 1 successeur d'un ordinal α ; - ceux de la forme
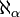 , indexés par un ordinal α limite et qui sont singuliers ;
, indexés par un ordinal α limite et qui sont singuliers ; - ceux de la forme
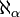 , indexés par un ordinal α limite et qui sont réguliers.
, indexés par un ordinal α limite et qui sont réguliers.
Ce dernier type de cardinal est qualifié de faiblement inaccessibles car ils ne peuvent être construits à partir de cardinaux plus petits. On distingue parmi eux les cardinaux fortement inaccessibles qui vérifient de plus
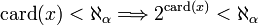 . L'existence de tels cardinaux ne peut se déduire des axiomes de la théorie des ensembles ZFC.
. L'existence de tels cardinaux ne peut se déduire des axiomes de la théorie des ensembles ZFC.
Les deux premiers types de cardinaux sont qualifiés au contraire d'accessibles, car on peut les construire (dans ZFC) à partir de cardinaux plus petits qu'eux.Hypothèse du continu
L'inégalité
 montrée ci-dessus permet d'écrire
montrée ci-dessus permet d'écrire 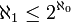 puisque
puisque 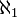 est le plus petit cardinal strictement supérieur à
est le plus petit cardinal strictement supérieur à 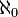 .
.L'hypothèse du continu affirme l'égalité
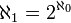 . On montre que cette propriété est indécidable dans ZFC. Par extension, l'hypothèse généralisée du continu énonce que, pour tout ordinal α, on a
. On montre que cette propriété est indécidable dans ZFC. Par extension, l'hypothèse généralisée du continu énonce que, pour tout ordinal α, on a  .
.Les résultats suivants s'obtiennent en admettant comme axiome l'hypothèse généralisée du continu.
- L'axiome du choix est démontrable.
- Il y a équivalence entre les notions de cardinaux faiblement inaccessibles et fortement inaccessibles.
- En notant
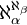 l'ensemble des fonctions de
l'ensemble des fonctions de 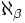 dans
dans  , il vient
, il vient
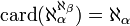 si
si 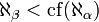 ;
;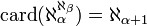 si
si 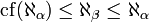 ;
;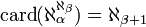 si
si 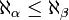 .
.
Notes et références
- ↑ R. Maillard, G. Girard, A. Lentin, Mathématiques, classe de seconde, 1964
Voir aussi
- Algèbre générale
- Correspondance et relation
- Nombre ordinal
- Théorie des ensembles
- Théorème de Cantor
- Beth (nombre)
- Aleph (nombre)
- Portail des mathématiques
Catégories : Théorie des ensembles | Nombre cardinal
Wikimedia Foundation. 2010.