- Fonction De Répartition
-
Fonction de répartition
En théorie des probabilités ou en statistiques, la fonction de répartition d'une variable aléatoire réelle caractérise la loi de probabilité de cette variable aléatoire réelle. La fonction de répartition de la variable aléatoire réelle
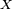 est la fonction
est la fonction 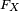 qui à tout réel
qui à tout réel  associe
associe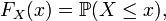
où le membre de droite réprésente la probabilité que la variable aléatoire réelle
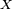 prenne une valeur inférieure ou égale à
prenne une valeur inférieure ou égale à  La probabilité que
La probabilité que 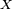 se trouve dans l'intervalle
se trouve dans l'intervalle ![\ \scriptstyle ]a, b]\](/pictures/frwiki/100/d222a4a91997a6c8e8e5fd493438dccd.png) est donc, si
est donc, si 
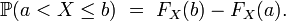
La fonction de répartition d'une mesure de probabilité
 définie sur la tribu borélienne
définie sur la tribu borélienne 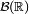 est la fonction
est la fonction 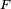 qui à tout réel
qui à tout réel  associe
associe![F(x) = \mathbb{P}(]-\infty, x]).](/pictures/frwiki/53/57ec4f5b8b6fb7931aa32b030458ef10.png)
Sommaire
Exemples de calculs de la fonction de répartition
Variables à densité
La fonction de répartition
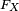 d'une variable aléatoire
d'une variable aléatoire 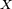 de densité de probabilité
de densité de probabilité  est une des primitives (en un sens un peu relaché, voir ci-dessous) de cette densité
est une des primitives (en un sens un peu relaché, voir ci-dessous) de cette densité  . Plus précisément
. Plus précisément 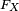 est définie par:
est définie par: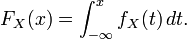
Toutefois, ce n'est pas, en toute généralité, une primitive au sens strict du terme : on peut seulement affirmer
- qu'une fonction de répartition
 est dérivable presque partout (pour la mesure de Lebesgue),
est dérivable presque partout (pour la mesure de Lebesgue), - que si la variable
 est à densité, alors la dérivée de
est à densité, alors la dérivée de  est presque partout (pour la mesure de Lebesgue) égale à
est presque partout (pour la mesure de Lebesgue) égale à 
Mais il y a beaucoup de "contre-exemples" : la fonction de répartition de la loi uniforme sur un intervalle, ou encore celle de la loi exponentielle, ne sont pas dérivables sur tout
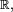 et ne sont donc pas, au sens strict, des primitives de densités de probabilités.
et ne sont donc pas, au sens strict, des primitives de densités de probabilités.Notons que, contrairement aux variables discrètes, une variable à densité X vérifie
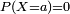 pour tout nombre réel a : en conséquence, la fonction de répartition des variables à densité est continue en tout point. En fait une variable aléatoire réelle X possède une densité de probabilité si et seulement si sa fonction de répartition est absolument continue sur chaque intervalle.
pour tout nombre réel a : en conséquence, la fonction de répartition des variables à densité est continue en tout point. En fait une variable aléatoire réelle X possède une densité de probabilité si et seulement si sa fonction de répartition est absolument continue sur chaque intervalle.Variables discrètes
Une variable aléatoire
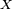 est dite discrète s'il existe un ensemble
est dite discrète s'il existe un ensemble  fini ou dénombrable tel que
fini ou dénombrable tel que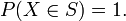
La loi de
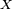 est déterminée sans ambiguité par la donnée de
est déterminée sans ambiguité par la donnée de  , où
, oùps = P(X = s). Si, par exemple,
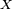 est une variable aléatoire réelle, on a
est une variable aléatoire réelle, on a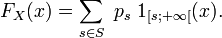
où
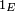 est la fonction indicatrice de l'ensemble E.
est la fonction indicatrice de l'ensemble E.Pour les variables aléatoires discrètes les plus courantes (par exemple, les lois uniformes, binomiales, de Poisson)
 est un ensemble bien ordonné : on peut alors numéroter ses éléments de manière croissante, p.e.
est un ensemble bien ordonné : on peut alors numéroter ses éléments de manière croissante, p.e. 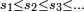 et numéroter les probabilités
et numéroter les probabilités 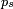 en conséquence, p.e. en posant
en conséquence, p.e. en posant 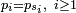 . On a alors, si
. On a alors, si 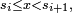
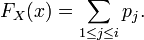
Soit encore, plus généralement :
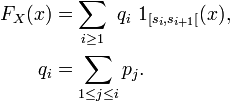
La fonction de répartition est alors une fonction constante par intervalles et sa représentation graphique est en escalier. Les sauts d'une marche à l'autre de l'escalier se situent aux abscisses
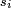 , et l'amplitude du saut d'abscisse
, et l'amplitude du saut d'abscisse  est
est  En particulier la fonction de répartition d'une variable discrète X est discontinue exactement aux points s tels que
En particulier la fonction de répartition d'une variable discrète X est discontinue exactement aux points s tels que  Voir la section Propriétés de la fonction de répartition pour une démonstration.
Voir la section Propriétés de la fonction de répartition pour une démonstration.Miscellanées
L'escalier de Cantor est un exemple de fonction de répartition continue mais dont la dérivée est presque partout nulle. Ainsi, la formule précédente ne vaut pas pour l'escalier de Cantor : bien que la loi de probabilité associée à l'escalier de Cantor soit diffuse (sans atome), cette loi ne possède pas de densité. L'escalier de Cantor est en fait un exemple de fonction de répartition continue mais qui n'est pas absolument continue sur chaque intervalle.
Propriétés de la fonction de répartition
Propriétés caractéristiques
Théorème — La fonction de répartition d'une variable aléatoire
 a les propriétés caractéristiques suivantes :
a les propriétés caractéristiques suivantes :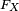 est croissante ;
est croissante ;- Elle est partout continue à droite ;
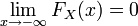 ;
;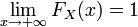 .
.
DémonstrationLe point 1 découle de la propriété de croissance des mesures de probabilité
![\{x\le y\}\Rightarrow\{]-\infty, x]\ \subset\ ]-\infty, y]\}\Rightarrow\{\mathbb{P}_{X}(]-\infty, x])\le\mathbb{P}_{X}(]-\infty, y])\}.](/pictures/frwiki/98/b4c475303f5772c740862a3d88198d59.png)
Comme
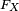 est monotone, le point 2 se réduit à montrer que
est monotone, le point 2 se réduit à montrer que
ou encore, équivalemment,
![\lim_{n}\mathbb{P}_{X}\left(\left]-\infty, x+\tfrac{1}{n}\right]\right)=\mathbb{P}_{X}\left(\left]-\infty, x\right]\right).](/pictures/frwiki/49/120df34deef4cb55a4243ad04db97d06.png)
Mais les boréliens
![\scriptstyle \ \left]-\infty, x+\tfrac{1}{n}\right]\](/pictures/frwiki/100/d160c4365d3625f7eebf900d2eb8101e.png) forment une suite décroissante, et
forment une suite décroissante, et![\bigcap_{n\ge 1}\left]-\infty, x+\tfrac1n\right]\ =\ \left]-\infty, x\right],](/pictures/frwiki/102/ffad7c55f19bbad3e5270073a541c74e.png)
donc le point 2 est une conséquence des axiomes des probabilités. Comme
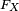 est monotone, le point 3 se réduit à montrer que
est monotone, le point 3 se réduit à montrer que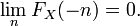
Ceci est encore une conséquence des axiomes des probabilités, puisque
![\bigcap_{n\ge 1}\left]-\infty, -n\right]\ =\ \emptyset.](/pictures/frwiki/102/f9a54fdec983c67655f0bc598e48c6e3.png)
Le point 4 découle, de la même manière, de
![\bigcup_{n\ge 1}\left]-\infty, n\right]\ =\ \R.](/pictures/frwiki/97/a6e48f3d1cc0a1b30c4dcdb4de99edc8.png)
Comme on l'a dit, les points 1 à 4 sont caractéristiques de la fonction de répartition d'une variable aléatoire réelle
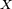 : étant donné une fonction réelle de la variable réelle, notons la
: étant donné une fonction réelle de la variable réelle, notons la 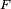 , satisfaisant les points 1 à 4, on peut construire concrètement une variable aléatoire réelle
, satisfaisant les points 1 à 4, on peut construire concrètement une variable aléatoire réelle 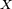 ayant
ayant 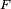 pour fonction de répartition, voir ci-dessous le théorème de la réciproque. Notons que cette construction sert à produire, sur ordinateur, des échantillons de taille arbitraire d'une loi de probabilité arbitraire, ce qui est l'ingrédient de base des méthodes de Monte-Carlo.
pour fonction de répartition, voir ci-dessous le théorème de la réciproque. Notons que cette construction sert à produire, sur ordinateur, des échantillons de taille arbitraire d'une loi de probabilité arbitraire, ce qui est l'ingrédient de base des méthodes de Monte-Carlo.Autres propriétés
A cause des points 1, 3 et 4,
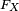 est bornée, plus précisément
est bornée, plus précisément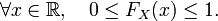
Comme toute fonction monotone bornée,
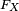 admet en tout point
admet en tout point  une limite à gauche
une limite à gauche 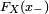 , limite à gauche égale ou non à
, limite à gauche égale ou non à 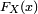 selon que
selon que 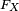 est continue en
est continue en  ou non. L'ensemble des points de discontinuité de
ou non. L'ensemble des points de discontinuité de 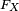 est fini ou dénombrable.
est fini ou dénombrable.La connaissance de la fonction de répartition permet de définir la probabilité de tout intervalle
-
- par passage au complémentaire,
-
- où l'on utilise
 pour
pour ![\scriptstyle \ A=]- \infty;x]\](/pictures/frwiki/56/81fba202958a5207fe1f320317bb9675.png) et
et ![\scriptstyle \ B=]- \infty;y],\](/pictures/frwiki/49/1533dccb867647725c2a88b08f73716d.png)
- où l'on utilise
-
- Cette propriété est la plus délicate et fait intervenir une conséquence des axiomes des probabilités sur la probabilité de l'union d'une suite croissante d'ensembles. On considère une suite
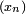 de réels croissante, convergeant vers x. L'intervalle
de réels croissante, convergeant vers x. L'intervalle ![\scriptstyle \ ]- \infty ; x[\](/pictures/frwiki/102/f9e7fbc4f20f40047f968edc75a4c89c.png) est alors union dénombrable de la suite croissante d'intervalles
est alors union dénombrable de la suite croissante d'intervalles ![\scriptstyle \ ]- \infty ; x_{n}]](/pictures/frwiki/51/3c90d17f4e0b367ec2375976360cb6fb.png) . La probabilité de l'intervalle
. La probabilité de l'intervalle ![\scriptstyle \ ]- \infty ; x[\](/pictures/frwiki/102/f9e7fbc4f20f40047f968edc75a4c89c.png) est donc la limite des probabilités des intervalles
est donc la limite des probabilités des intervalles ![\scriptstyle \ ]- \infty ; x_{n}]](/pictures/frwiki/51/3c90d17f4e0b367ec2375976360cb6fb.png) , i.e. la limite de la suite
, i.e. la limite de la suite 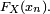 Par propriété des fonctions croissantes, cette limite existe et vaut
Par propriété des fonctions croissantes, cette limite existe et vaut 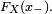
- Cette propriété est la plus délicate et fait intervenir une conséquence des axiomes des probabilités sur la probabilité de l'union d'une suite croissante d'ensembles. On considère une suite
![P(X \in ]x;y[ )\,=\,P(x < X < y)\,=\,= F_X(y_-)-F_X(x),](/pictures/frwiki/50/2c6762362f417053e45e06c892c17171.png)
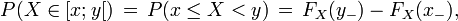
![P(X \in [x;y])\,=\,P(x \le X \le y)\,=\,F_X(y) - F_X(x_-),](/pictures/frwiki/99/ce63ede7d5a3aaf1e9ef1de86c0f367e.png)
- En particulier
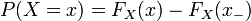
-
- ces 4 dernières propriétés découlant de
 pour différents choix de
pour différents choix de  et
et 
- ces 4 dernières propriétés découlant de
On appelle atome de la variable aléatoire X tout réel a pour lequel![\scriptstyle \ P[X=a]>0](/pictures/frwiki/51/351883ce7e7ade6bdd61ed0ef8401650.png) . Ainsi les atomes de la variable aléatoire X sont exactement les points de discontinuité de la fonction de répartition.
. Ainsi les atomes de la variable aléatoire X sont exactement les points de discontinuité de la fonction de répartition.La fonction de répartition d'une variable aléatoire
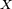 est donc continue si et seulement si X n'a aucun atome, i.e. si et seulement si
est donc continue si et seulement si X n'a aucun atome, i.e. si et seulement si![\forall x\in\mathbb{R},\ P[X = x]=0.](/pictures/frwiki/99/c10069f9caf35ebbdf66ee3a950c5986.png)
On dit alors que la loi de
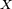 est diffuse, ou bien sans atome, et, par extension, que la variable aléatoire
est diffuse, ou bien sans atome, et, par extension, que la variable aléatoire 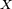 elle-même est diffuse ou sans atome. En particulier, les variables aléatoires réelles possédant une densité de probabilité sont diffuses. Il existe cependant des variables aléatoires diffuses mais ne possédant pas pour autant une densité de probabilité, c'est le cas, par exemple, de la variable aléatoire ayant pour fonction de répartition l'escalier de Cantor.
elle-même est diffuse ou sans atome. En particulier, les variables aléatoires réelles possédant une densité de probabilité sont diffuses. Il existe cependant des variables aléatoires diffuses mais ne possédant pas pour autant une densité de probabilité, c'est le cas, par exemple, de la variable aléatoire ayant pour fonction de répartition l'escalier de Cantor.Caractérisation de la loi par la fonction de répartition
Théorème — La loi de probabilité d'une variable aléatoire réelle est caractérisée par sa fonction de répartition.
Ou bien encore : si deux variables aléatoires réelles ont même fonction de répartition, alors elles ont même loi (et réciproquement).
DémonstrationSous l'hypothèse
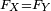 , on peut démontrer de manière élémentaire que
, on peut démontrer de manière élémentaire que 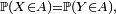 dès que
dès que  est un borélien "simple" (par exemple, si
est un borélien "simple" (par exemple, si  est un intervalle). Par contre, la démonstration générale (pour tout borélien
est un intervalle). Par contre, la démonstration générale (pour tout borélien  ) est un cas particulier du lemme d'unicité des probabilités, lui-même corrolaire du lemme de classe monotone, appliqué à la classe
) est un cas particulier du lemme d'unicité des probabilités, lui-même corrolaire du lemme de classe monotone, appliqué à la classeIl faut vérifier que
- la classe
 est stable par intersection finie,
est stable par intersection finie, - la tribu engendrée par
 contient (et en fait est égale à) la tribu borélienne.
contient (et en fait est égale à) la tribu borélienne.
Le lemme d'unicité des probabilités permet alors de conclure.
Vérifions 1. Soit
 une partie finie de
une partie finie de 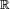 . Soit
. Soit  l'élément minimal de
l'élément minimal de  . Alors
. AlorsVérifions 2. La tribu engendrée par
 est notée
est notée 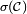 . La tribu borélienne est notée
. La tribu borélienne est notée 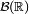 , comme souvent. Notons
, comme souvent. NotonsOn a
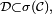 en vertu de la stabilité des tribus par passage au complémentaire, donc
en vertu de la stabilité des tribus par passage au complémentaire, donc 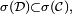 par définition d'une tribu engendrée. On peut interchanger
par définition d'une tribu engendrée. On peut interchanger  et
et 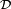 dans ce qui précède, donc, par double inclusion,
dans ce qui précède, donc, par double inclusion,Comme
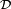 est une partie de l'ensemble des ouverts, on en déduit que
est une partie de l'ensemble des ouverts, on en déduit queMais il nous faut surtout démontrer l'inclusion en sens inverse, et, pour cela, démontrer que tout ouvert de
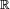 est dans
est dans 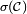 (ainsi
(ainsi 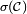 est une tribu contenant tous les ouverts de
est une tribu contenant tous les ouverts de 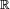 , alors que
, alors que 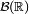 est la plus petite tribu contenant tous les ouverts de
est la plus petite tribu contenant tous les ouverts de 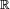 ). Un argument rapide est de constater que
). Un argument rapide est de constater que- tout ouvert de
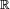 est réunion dénombrable d'intervalles ouverts, et que
est réunion dénombrable d'intervalles ouverts, et que - les intervalles ouverts sont dans
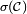 .
.
Le premier point résulte de ce que
- un ouvert
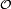 est réunion disjointe de ses composantes connexes (cela est vrai pour toute partie de
est réunion disjointe de ses composantes connexes (cela est vrai pour toute partie de 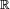 ),
), - les parties connexes de
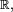 (et en particulier les composantes connexes ci-dessus) sont exactement les intervalles de
(et en particulier les composantes connexes ci-dessus) sont exactement les intervalles de 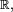
- comme
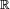 est localement connexe, les composantes connexes d'un ouvert sont automatiquement ouvertes.
est localement connexe, les composantes connexes d'un ouvert sont automatiquement ouvertes. - dans chaque composante connexe
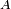 de notre ouvert
de notre ouvert 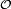 , on peut choisir un nombre rationnel
, on peut choisir un nombre rationnel 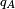 . Les
. Les 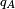 sont distincts car les composantes sont disjointes. Ainsi
sont distincts car les composantes sont disjointes. Ainsi 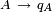 est une bijection entre la famille des composantes connexes de
est une bijection entre la famille des composantes connexes de 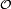 et une partie de
et une partie de 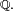 La famille des composantes connexes de
La famille des composantes connexes de 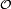 est donc finie ou dénombrable.
est donc finie ou dénombrable.
Le deuxième point tient à ce que
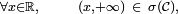 comme on l'a vu plus haut ;
comme on l'a vu plus haut ;![\scriptstyle\forall y\in\mathbb{R},\qquad(-\infty,y)\ =\ \bigcup_{n\ge 1}\ \left(-\infty,y-\tfrac1n\right]\ \in\ \sigma (\mathcal{C})\](/pictures/frwiki/51/32252fdd789e5127db4e92989c248077.png) ;
;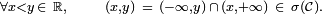
CQFD
En d'autres termes, si deux variables aléatoires réelles,
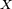 et
et 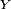 , vérifient
, vérifientalors elles vérifient aussi que pour tout borélien
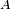 ,
,De plus, elles vérifient que pour toute fonction mesurable
 ,
,dès que l'un des deux termes de l'égalite a un sens.
Théorème de la réciproque
Soit
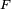 une fonction de
une fonction de 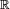 dans
dans 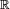 satisfaisant les 4 propriétés caractéristiques. Notons
satisfaisant les 4 propriétés caractéristiques. Notons 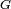 la fonction définie pour
la fonction définie pour ![\ \scriptstyle \omega \in]0,1[\](/pictures/frwiki/52/4e14c719119402d051260b885dc74f70.png) par
par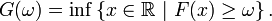
Alors
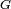 est une variable aléatoire réelle définie sur l'espace probabilisé
est une variable aléatoire réelle définie sur l'espace probabilisé 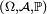 où
où ![\ \scriptstyle \left(\Omega,\mathcal{A}\right)=\left(]0,1[,\mathcal{B}(]0,1[)\right)\](/pictures/frwiki/48/01ebc3908a0f4365553f75ec2ef257ec.png) et où
et où  désigne la restriction à
désigne la restriction à ![\ \scriptstyle \mathcal{B}(]0,1[)\](/pictures/frwiki/48/0d41c4a896252b147406cbca239c0c4b.png) de la mesure de Lebesgue sur
de la mesure de Lebesgue sur 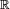 . Le théorème stipule que :
. Le théorème stipule que :Théorème — Sur l'espace
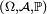 , la fonction de répartition de
, la fonction de répartition de 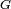 est
est 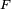 .
.Ainsi toute fonction
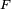 de
de 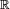 dans
dans 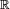 satisfaisant les 4 propriétés caractéristiques est fonction de répartition d'une variable aléatoire réelle (de
satisfaisant les 4 propriétés caractéristiques est fonction de répartition d'une variable aléatoire réelle (de 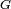 , par exemple), ou encore d'une mesure de probabilité sur
, par exemple), ou encore d'une mesure de probabilité sur 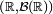 (de la loi de
(de la loi de  , par exemple).Démonstration
, par exemple).DémonstrationDémonstration
Pour
![\ \scriptstyle \omega \in \Omega=]0,1[\](/pictures/frwiki/56/809bc065eb7f15f2d5eabdddb7f61c18.png) , notons
, notons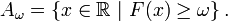
Donc
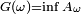 . A cause du point 4,
. A cause du point 4,  , et à cause du point 3,
, et à cause du point 3, 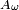 est bornée inférieurement, donc
est bornée inférieurement, donc 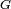 est bien définie.
est bien définie.Commençons par un cas simple à titre d'entrainement:
F est continue strictement croissante
Si
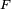 est continue strictement croissante sur
est continue strictement croissante sur 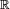 , alors
, alors 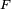 est une bijection de
est une bijection de 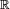 dans ]0,1[, et
dans ]0,1[, et 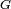 est la réciproque de
est la réciproque de 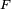 (on peut s'en convaincre en traçant
(on peut s'en convaincre en traçant 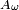 à l'aide du graphe de
à l'aide du graphe de 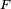 ). A ce titre,
). A ce titre, 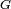 est continue et strictement croissante sur ]0,1[, et en particulier
est continue et strictement croissante sur ]0,1[, et en particulier 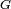 est mesurable (c'est donc une v.a.r.). On a, de plus,
est mesurable (c'est donc une v.a.r.). On a, de plus,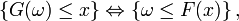
donc
![\begin{align}
\left\{\omega\in\Omega\ |\ G(\omega)\le x\right\}
&=
\left\{\omega\in\Omega\ |\ \omega\le F(x)\right\}
\\
&=
]0, F(x)].
\end{align}](/pictures/frwiki/51/35865cf34891acce296bfba75db07b0a.png)
Ainsi
![\mathbb{P}\left(G\le x\right)
=
\mathbb{P}(]0, F(x)])
=F(x).](/pictures/frwiki/57/98fe2fd37fd2810bf1ff9d6a14f0c56f.png) Démonstration dans le cas général
Démonstration dans le cas généralCas général
Dans le cas général, on a également
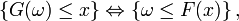
et on conclut donc exactement de la même manière que précédemment, mais la démonstration de l'équivalence ci-dessus est moins directe. Tout d'abord, pour
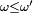 ,
, 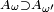 , et donc
, et donc 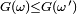 . Du fait que
. Du fait que 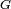 est monotone, il résulte que
est monotone, il résulte que 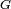 est mesurable.
est mesurable.On a, par définition de
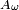 et de
et de 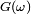 ,
,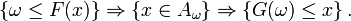
La réciproque vient de ce que
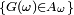 , i.e.
, i.e. 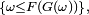 ce qui, avec
ce qui, avec 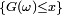 entraîne, par croissance de
entraîne, par croissance de 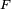 ,
, 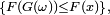 et finalement
et finalement 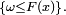 Supposons en effet que
Supposons en effet que  , et considérons une suite strictement décroissante
, et considérons une suite strictement décroissante 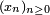 d'éléments de
d'éléments de 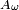 telle que
telle que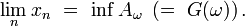
Par continuité à droite de
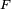 ,
,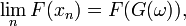
mais également, par définition de
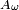 ,
,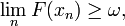
ce qui conduit à
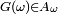 , d'où une contradiction (démonstration largement reprise de Sidney Resnick, A Probability Path).
, d'où une contradiction (démonstration largement reprise de Sidney Resnick, A Probability Path).Remarques.
- Lorsque
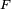 est une bijection bicontinue d'un intervalle
est une bijection bicontinue d'un intervalle  dans
dans ![\ \scriptstyle ]0,1[\](/pictures/frwiki/48/0bb723693494c23859b5b32a93be9ee7.png) (i.e.
(i.e. 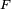 est continue strictement croissante),
est continue strictement croissante), 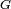 est tout simplement la réciproque de
est tout simplement la réciproque de 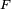 (i.e.
(i.e. 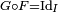 et
et ![\ \scriptstyle F\circ G=\text{Id}_{]0,1[}\](/pictures/frwiki/97/a96a69b025c97cfff1156bca6707afba.png) ). Pour cette raison,
). Pour cette raison, 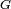 est parfois appelée réciproque généralisée de
est parfois appelée réciproque généralisée de 
- L'intérêt pratique de ce Théorème est développé dans l'article Méthode de la transformée inverse, ainsi que dans la section suivante.
Conséquences du théorème de la réciproque
Simulation de variables aléatoires réelles de loi arbitraire
- Si
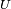 désigne une variable aléatoire réelle uniforme sur [0,1], alors
désigne une variable aléatoire réelle uniforme sur [0,1], alors 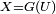 a pour fonction de répartition
a pour fonction de répartition 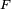 .
.
Ainsi dans tout langage de programmation possédant un générateur de nombres aléatoires, on peut simuler une suite de longueur arbitraire de v.a.r. indépendantes de même fonction de répartition
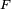 , pourvu que
, pourvu que 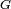 soit connue : il suffit alors d'appeler ce générateur de manière répétée, et d'appliquer la fonction
soit connue : il suffit alors d'appeler ce générateur de manière répétée, et d'appliquer la fonction 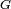 aux nombres produits par ces appels répétés.
aux nombres produits par ces appels répétés.Exemples
Exemples densité de probabilité fonction de répartition réciproque (généralisée) code Loi de Cauchy 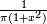
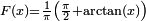
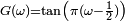
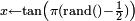
Loi exponentielle 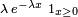
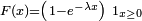
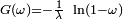
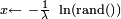
Loi uniforme sur [a,b] ![\scriptstyle \frac{1}{b-a}\ 1_{[a,b]}(x)](/pictures/frwiki/54/6f7f36df35625486b62d364b7ef0e3bd.png)
![\scriptstyle F(x)=\frac{x-a}{b-a}\ 1_{[a,b]}(x)\ +\ 1_{]b,+\infty[}(x)](/pictures/frwiki/49/1c678be4753c5a108f50b77bd6d99bf4.png)

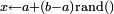
Loi de Bernoulli 
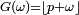
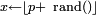
Loi uniforme sur 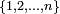
![\scriptstyle F(x)=\left\lfloor\frac{x}{n}\right\rfloor\ 1_{[0,1]}(x)\ +\ 1_{]1,+\infty[}(x)](/pictures/frwiki/97/a4149ce6247bd14b4b417621e26c7bde.png)
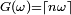
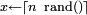
Loi normale, Loi binomiale comme il n'y a pas de formule suffisamment explicite pour la fonction de répartition, et encore moins de formule explicite pour la réciproque de cette dernière, le théorème est alors inopérant. Autres conséquences du théorème de la réciproque
La réciproque généralisée de
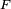 est un exemple de v.a.r. dont la fonction de répartition est
est un exemple de v.a.r. dont la fonction de répartition est 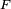 , mais c'est un exemple privilégié. Ses utilisations sont nombreuses, allant de propriétés de l'ordre stochastique, à des propriétés de la distance de Wasserstein [1], en passant par le théorème de représentation de Skorohod, voir section suivante.
, mais c'est un exemple privilégié. Ses utilisations sont nombreuses, allant de propriétés de l'ordre stochastique, à des propriétés de la distance de Wasserstein [1], en passant par le théorème de représentation de Skorohod, voir section suivante.Convergence en loi et fonction de répartition
Considérons une suite de variables aléatoires
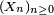 (resp. une variable aléatoire
(resp. une variable aléatoire 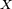 ) définies sur des espaces probabilisés
) définies sur des espaces probabilisés 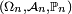 (resp.
(resp.  ) éventuellement différents, mais toutes à valeurs dans le même espace métrique
) éventuellement différents, mais toutes à valeurs dans le même espace métrique 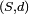 . On dit que
. On dit que 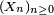 converge en loi vers
converge en loi vers 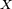 ssi, pour toute fonction continue bornée de
ssi, pour toute fonction continue bornée de 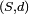 dans
dans 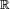 ,
,On a le théorème suivant :
Théorème — Dans le cas de variables aléatoires réelles (
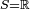 ), notons
), notons 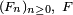 les fonctions de répartitions de
les fonctions de répartitions de 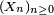 et de
et de 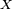 . Il y a alors équivalence entre les 3 propositions ci-dessous :
. Il y a alors équivalence entre les 3 propositions ci-dessous :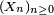 converge en loi vers
converge en loi vers 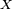 ,
,- pour tout réel
 en lequel
en lequel 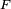 est continue,
est continue,  ,
, - il existe un espace probabilisé
 , et, définies sur cet espace, des variables aléatoires réelles
, et, définies sur cet espace, des variables aléatoires réelles 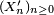 et
et 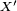 telles que, simultanément,
telles que, simultanément,
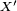 a même loi que
a même loi que 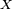 ,
,- pour chaque
 ,
, 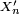 a même loi que
a même loi que 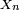 ,
, 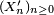 converge presque sûrement vers
converge presque sûrement vers 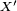 .
.
L'implication 1.
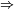 3. reste vraie lorsque les variables aléatoires réelles sont remplacées par des variables aléatoires à valeurs dans un espace de Lusin
3. reste vraie lorsque les variables aléatoires réelles sont remplacées par des variables aléatoires à valeurs dans un espace de Lusin  , i.e. un espace métrisable assez général (
, i.e. un espace métrisable assez général ( et
et ![\scriptstyle\ S=\mathcal{C}([0,1],\mathbb{R})\](/pictures/frwiki/54/6bfa0c17e2d85d990761d80db4faf50e.png) en sont des exemples). L'implication 1.
en sont des exemples). L'implication 1. 3. porte alors le nom de Théorème de représentation de Skorohod.Démonstration
3. porte alors le nom de Théorème de représentation de Skorohod.DémonstrationUne structure possible pour la démonstration est 3.
 1.
1. 2.
2. 3.
3.3. implique 1.
C'est le plus simple. Il faut démontrer que
ou bien, équivalemment,
Mais la continuité de
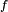 assure que
assure que 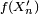 converge presque sûrement vers
converge presque sûrement vers 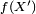 . De plus,
. De plus, 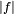 étant borné, on a que
étant borné, on a quepour tout
 . Le théorème de convergence dominée de Lebesgue peut donc être appliqué ici, et donne la conclusion voulue.
. Le théorème de convergence dominée de Lebesgue peut donc être appliqué ici, et donne la conclusion voulue.1. implique 2.
On utilise la famille de fonctions continues bornées
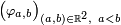 définies par le graphe ci-contre. Elles vérifient, pour toute variable aléatoire réelle
définies par le graphe ci-contre. Elles vérifient, pour toute variable aléatoire réelle 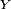 ,
,et en particulier
On remarque alors que, pour tout
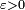 ,
,et
En faisant tendre
 vers 0, on obtient
vers 0, on obtientAinsi, dès que
 est un point de continuité de
est un point de continuité de 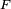 ,
,2. implique 3.
Notons
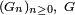 , les réciproques généralisées de
, les réciproques généralisées de 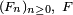 . Pour le triplet
. Pour le triplet  , choisissons
, choisissons 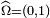 , et prenons pour
, et prenons pour  la tribu des boréliens et la mesure de Lebesgue correspondantes (i.e. restreintes à
la tribu des boréliens et la mesure de Lebesgue correspondantes (i.e. restreintes à 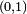 ). Le choix de
). Le choix de 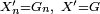 satisfait à 3.1. et à 3.2. en vertu du théorème de la réciproque. De plus, en conséquence de 2.,
satisfait à 3.1. et à 3.2. en vertu du théorème de la réciproque. De plus, en conséquence de 2., 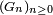 converge presque sûrement vers
converge presque sûrement vers 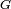 (mais cela mériterait d'être développé).
(mais cela mériterait d'être développé).Voir aussi
- Article principal : Variable aléatoire
- Convergence de variables aléatoires
- Convergence en loi
- en:Wasserstein metric
- Inégalité de réarrangement
- Portail des probabilités et des statistiques
Catégorie : Probabilités - qu'une fonction de répartition
Wikimedia Foundation. 2010.


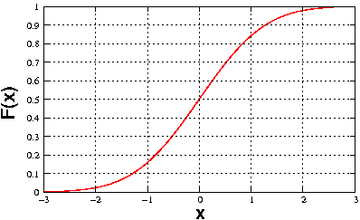

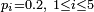 , en bleu) et de la loi uniforme sur l'intervalle [0,1] (en rouge)
, en bleu) et de la loi uniforme sur l'intervalle [0,1] (en rouge)![P(X \in ]- \infty;x])\,=\,P(X \le x)\,=\,F_X(x),](/pictures/frwiki/57/964b972abf0511deccbfe1385e6808e2.png)
![P(X \in ]x; + \infty[)\,=\,P(X >x)\,=\,1-F_X(x),](/pictures/frwiki/101/e59ebbcc8b457959cbdb2e7bdb40fa75.png)
![P(X \in ]x;y])\,=\,P(x < X \le y)\,=\,F_X(y) - F_X(x),](/pictures/frwiki/57/94ceb8a34851764d5f80ebd0d0594f66.png)
![P(X \in ]- \infty;x[)\,=\,P(X <x)\,=\,F_X(x_-),](/pictures/frwiki/101/e0b87b999446176c0481f9c6a2abfa6d.png)
![\mathcal{C}=\left\{(-\infty,x]\ |\ x\in\mathbb{R}\right\}.](/pictures/frwiki/56/824c50068bcfc140b8f1239e2035170c.png)
![\bigcap_{x\in I}(-\infty,x]\,=\,(-\infty,y]\ \in\ \mathcal{C}.](/pictures/frwiki/55/7952beeabcc2bdb7e4adec85b51dce25.png)

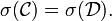
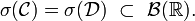
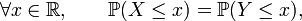
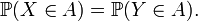
![\ \qquad \mathbb{E}[\varphi(X)]=\mathbb{E}[\varphi(Y)],](/pictures/frwiki/52/4cf91938d6d9b4e99480c9c2a118f03f.png)
![\lim_{n\rightarrow\infty} \mathbb{E}\left[f(X_n)\right]=\mathbb{E}\left[f(X)\right].](/pictures/frwiki/49/123a852d461b7018f77048988255945d.png)
![\lim_{n\rightarrow\infty} \mathbb{E}\left[f(X_n)\right]=\mathbb{E}\left[f(X)\right],](/pictures/frwiki/97/a9615e3f6607884ee583899e6b26d2d3.png)
![\lim_{n\rightarrow\infty} \mathbb{E}\left[f(X^{\prime}_n)\right]=\mathbb{E}\left[f(X^{\prime})\right].](/pictures/frwiki/57/9520be37c6da8c06a3f309f6e4f5302d.png)
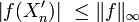

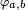 .
.![\mathbb{P}\left(Y\le a\right)
\le
\mathbb{E}\left[\varphi_{a,b}(Y)\right]
\le
\mathbb{P}\left(Y\le b\right),](/pictures/frwiki/51/38e77e6b67836cec541be22f6337ce93.png)
![\mathbb{E}\left[\varphi_{x-\varepsilon,x}(X_n)\right]
\le
F_n(x)
\le
\mathbb{E}\left[\varphi_{x,x+\varepsilon}(X_n)\right].](/pictures/frwiki/54/67b6e69b31d41500e1080c30af932a3b.png)
![\begin{align}
\limsup_n F_n(x)
&\le
\lim_n\mathbb{E}\left[\varphi_{x,x+\varepsilon}(X_n)\right]
\\
&=
\mathbb{E}\left[\varphi_{x,x+\varepsilon}(X)\right]
\le
\mathbb{P}\left(X\le x+\varepsilon\right)
=
F(x+\varepsilon),
\end{align}](/pictures/frwiki/54/6f45eb7cb008df5a9d54391991bc0543.png)
![\begin{align}
\liminf_n F_n(x)
&\ge
\lim_n\mathbb{E}\left[\varphi_{x-\varepsilon,x}(X_n)\right]
\\
&=
\mathbb{E}\left[\varphi_{x-\varepsilon,x}(X)\right]
\ge
\mathbb{P}\left(X\le x-\varepsilon\right)
=
F(x-\varepsilon).
\end{align}](/pictures/frwiki/50/297e02e4d9179c2a7095d8b8f109a9da.png)