- Equation differentielle stochastique
-
Équation différentielle stochastique
Une équation différentielle stochastique (EDS) est une généralisation de la notion d'équation différentielle prenant en compte un terme de bruit blanc. Les EDS permettent de modéliser des trajectoires aléatoires, tels des cours de bourse ou les mouvements de particules soumises à des phénomènes de diffusion. Elle permettent aussi de traiter théoriquement ou numériquement des problèmes issus de la théorie des équations aux dérivées partielles.Les domaines d'application des EDS sont vastes : physique, biologie, dynamique des populations, écologie, mathématiques financières, traitement du signal, théorie du contrôle, ...
Sommaire
Quelques approches et définitions informelles
Les EDS comme trajectoires de particules
Le mouvement brownien, nommé ainsi en hommage au botaniste Robert Brown, décrit le mouvement d'une particule soumise à une infinité de chocs en des temps très courts, et ses trajectoires sont erratiques. Elles ont les propriétés suivantes :
- Si l'on connaît la position de la particule à un instant t, alors la loi de sa position spatiale à un instant ultérieur t + s ne dépend que de sa position à cet instant t. Autrement dit, le passé, c'est-à-dire la trajectoire de la particule à des instants antérieurs à t, n'a aucune influence sur ses déplacements futurs. Cette propriété s'appelle la propriété de Markov.
- Les particules bougent continûment dans l'espace.
- La loi de la position de la particule entre deux instants t et t + s ne dépend que de s. Les accroissements sont alors stationnaires.
- En fait, si B(t) désigne la position de la particule à un instant t, alors le loi de B(t) − B(s) et de B(s) − B(r) avec s < r < t sont indépendants l'un de l'autre. Nous dirons alors que les accroissements sont indépendants. En fait, cette propriété implique la propriété de Markov.
- De ces deux derniers faits, et dans l'esprit du théorème central limite, il est alors possible de montrer que B(t) suit une loi normale de moyenne 0 et de variance t.
En d'autres termes, la dynamique de la particule est la même quelle que soit sa position dans l'espace, et si l'on tourne les coordonnées de l'espace à l'aide d'une rotation, un mouvement brownien reste un mouvement brownien : la particule évolue dans un environnement homogène et isotrope.
La notion d'EDS permet de décrire le mouvement d'une particule dans un milieu dont les propriétés physiques peuvent varier, en créant deux effets :
- Si nous connaissons la position X(t) d'une particule, la loi du processus à un instant t + δt est une gaussienne dont la covariance n'est pas nécessairement l'identité, et qui peut dépendre de la position X(t). La covariance doit être de l'ordre de δt.
- En temps très petit, les particules sont poussées dans une direction donnée. Nous parlerons alors de dérive. Cela implique en fait que la position moyenne de la particule à l'instant t + δt sachant la position X(t) est donnée par
![\mathbb{E}[X(t+\delta t)|X(t)]=\mu \delta t](/pictures/frwiki/56/8c5764dfe550ace6e2aaab7f9b824b06.png) pour un vecteur μ, qui peut aussi dépendre de X(t).
pour un vecteur μ, qui peut aussi dépendre de X(t).
En combinant ces deux effets, nous pouvons écrire
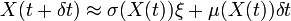 ,
,où ξ est une gaussienne normale centrée de covariance l'identité. L'on vérifie facilement que
![\mathbb{E}[X(t+\delta t)|X(t)]=\mu \delta t](/pictures/frwiki/56/8c5764dfe550ace6e2aaab7f9b824b06.png)
et
![\mathbb{E}[(X(t+\delta t)-\mathbb{E}[X(t+\delta t)|X(t)])^2]
=\sigma(X(t))\sigma(X(t))^{\mathrm{T}}\delta t](/pictures/frwiki/51/3083dc55323aaf24e248c8947bfbe255.png) .
.En partant de 0, et si l'on somme les accroissements entre kδt et (k + 1)δt, alors nous obtenons
 ,
,où ne faisons l'hypothèse que les variables gaussiennes ξk sont indépendantes, ce qui est assez raisonnable si nous souhaitons garder la propriété de Markov, c'est-à-dire l'indépendance de la loi des positions futures de la particule après t par rapport aux instant antérieurs à t. Nous pouvons prendre pour ξk les accroissements successifs d'un mouvement brownien.
À l'aide de la théorie des intégrales stochastiques, nous pouvons faire tendre δt vers 0 (attention, il s'agit ici d'une convergence en probabilité !), et considérer l'équation suivante
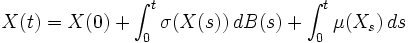 ,
,où B est un mouvement brownien, σ est une fonction à valeur matricielle (qui n'est pas forcément une matrice carrée), et μ une fonction à valeur vectorielle. Une telle équation, qui implique donc une intégrale stochastique, est appelée équation différentielle stochastique (EDS).
La théorie des EDS consiste donc à étudier les propriétés de cet objets, et les conditions sur les coefficients qui permettent d'assurer l'existence de tels objets.
Contrairement au mouvement brownien, les solutions d'EDS, sauf dans le cas simple où σ et μ sont constants, ne sont pas à accroissement indépendants et stationnaires. Par contre, elles possèdent bien la propriété de Markov.
Équations différentielles bruitées
Considérons une équation différentielle ordinaire
 à laquelle nous aimerions rajouter du bruit. Un bruit blanc ξ(t) sera utilisé comme modèle de bruit, dont l'intensité va varier en fonction de la position de l'espace, et notre équation devient alors
à laquelle nous aimerions rajouter du bruit. Un bruit blanc ξ(t) sera utilisé comme modèle de bruit, dont l'intensité va varier en fonction de la position de l'espace, et notre équation devient alors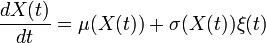
pour une fonction σ. En soi, un bruit blanc est un objet mal défini (cela correspond à un bruit aléatoire où toutes les fréquences sont présentes avec une égale probabilité), et une telle équation n'a pas de sens. Par contre, le bruit blanc étant défini formellement comme la dérivée du mouvement brownien B(t) nous transformons notre équation en

dont nous pouvons prouver qu'elle a bien un sens, à l'aide du calcul stochastique, lorsqu'elle est écrite sous forme intégrale :
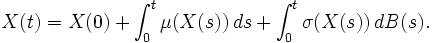
Les EDS comme limites d'équations différentielles ordinaires
Une autre façon naturelle pour considérer les EDS est d'utiliser des interpolations linéaires par morceaux des trajectoires d'un mouvement brownien. Soit B(t,ω) une telle trajectoire, et considérons entre l'instant 0 et l'instant T,
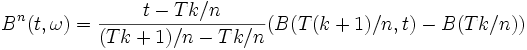 si
si ![t\in[Tk/n,T(k+1)/n]](/pictures/frwiki/55/77957a4dae8fcde6001139a17756da69.png)
ainsi que les équations différentielles ordinaires (sous de bonnes conditions de régularité sur σ et μ)
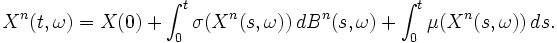
Pouvons-nous montrer que Xn(t,ω) converge quelque chose quand n tend vers l'infini ? En fait, cette approche fonctionne, mais la démonstration n'est pas évidente et comporte des chausses-trappes. En fait, Xn(t,ω) converge vers la solution d'une EDS au sens de Stratonovich
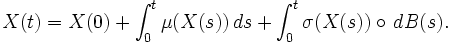
qui implique donc une autre notion d'intégrale stochastique, ici dénotée avec un
 , celle de Stratonovich. Ce résultat est du à Eugene Wong et Moshe Zakai. Si l'on souhaite utiliser une intégrale d'Itô, alors
, celle de Stratonovich. Ce résultat est du à Eugene Wong et Moshe Zakai. Si l'on souhaite utiliser une intégrale d'Itô, alors
Parmi les difficultés, il convient de noter qu'il est nécessaire, sauf en dimension un, d'utiliser une famille de partition déterministe si l'on souhaite utiliser autre chose qu'une partition régulière, ainsi qu'une interpolation linéaire par morceaux. pour que la convergence vers l'EDS attendue ait bien lieu.
Quelques EDS remarquables
Comme pour les équations différentielles ordinaires, nous ne savons pas résoudre une EDS dans le cas général.
Mouvement brownien géométrique
Le mouvement brownien géometrique est un processus de la forme
X(t) = X(0)exp(σB(t) + μt)
et est couramment utilisé en mathématiques financières pour modéliser l'évolution de cours de bourse (dans le modèle de Black-Scholes) par exemple. Grâce à la formule d'Itô, le mouvement brownien géométrique est solution de
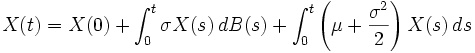 .
.L'équation de Langevin et le processus d'Ornstein-Uhlenbeck
L'équation de Langevin donne le mouvement d'une particule dans un milieu avec friction, et soumise à une force ξ(t) fluctuante (« bain thermique »), que nous prendrons comme un bruit blanc. D'après le principe fondamental de la dynamique, la vitesse de la particule est solution de
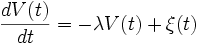 .
.Comme précédemment, cette équation n'a pas vraiment de sens, à moins de la poser sous la forme
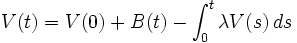 ,
,où B(t) est un mouvement brownien. Le paramètre λ spécifie l'intensité de la friction. Cette équation peut-être résolue directement :
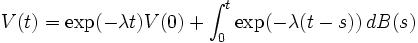
C'est un processus d'Ornstein-Uhlenbeck, et sa particularité est d'être un processus gaussien. Sa moyenne et sa variance sont
![\mathbb{E}[V(t)]=\exp(-\lambda t)V(0)](/pictures/frwiki/53/5355b831df3f2049f414c0cfc4df8848.png) et
et ![\mathbb{E}[(V(t)-V(0))^2]=\frac{1-\exp(-2\lambda t)}{2\lambda}](/pictures/frwiki/50/29b9f58d67e6749995e4d3b48cbd6660.png) .
.Notons qu'ici, nous avons considéré la vitesse de la particule. Sa position est donnée par
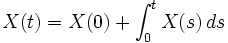 , et est en soi une trajectoire régulière, mais qui reste un processus gaussien.
, et est en soi une trajectoire régulière, mais qui reste un processus gaussien.En faisant tendre certains paramètres vers l'infini, alors nous pouvons approcher X(t) par une EDS
Particule aléatoire dans un champ de force
Nous pouvons raffiner l'équation de Langevin en ajoutant un champ de force qui dépend de la position. Alors la position et la vitesse de la particule sont solutions d' une équation que nous écrirons sous la forme
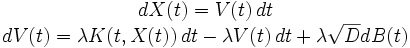 où λK est le champ de force considéré, et λ,D > 0. Il est alors possible de montrer que la position X(t), lorsque λ tend vers l'infini, se comporte elle-même comme la solution de l'EDS
où λK est le champ de force considéré, et λ,D > 0. Il est alors possible de montrer que la position X(t), lorsque λ tend vers l'infini, se comporte elle-même comme la solution de l'EDS
En application, si U est un potentiel, c'est-à-dire que son gradient est une force, alors
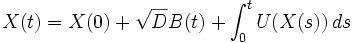
est une EDS couramment utilisée en physique. Sans la présence du mouvement brownien dans le modèle précédent, la particule sera immobilisée au fond des puits de U, c'est-à-dire là où le gradient
 est nul. En présence d'un bruit, même petit, elle a alors la possibilité de s'échapper et de passer d'un puits à l'autre, et de telles dynamiques sont souvent étudiées (on a parfois des phénomènes de résonance stochastique).
est nul. En présence d'un bruit, même petit, elle a alors la possibilité de s'échapper et de passer d'un puits à l'autre, et de telles dynamiques sont souvent étudiées (on a parfois des phénomènes de résonance stochastique).Pont brownien
La probabilité qu'un mouvement brownien atteigne un point donné à un temps fixé T est nulle. Cependant, on a parfois besoin de considérer la trajectoire d'un mouvement brownien (ici en une dimension) conditionnée par un tel événement. On peut construire un tel objet X(t) comme la solution de
![X(t)=a+B(t)+\int_0^t \frac{b-X(s)}{T-s}\, ds,\ t\in[0,T].](/pictures/frwiki/52/4a3cb85600bc488a4edb9f3f8736ef91.png)
Les trajectoires de X(t) partiront de a et atteindront le point b au temps T. Le processus X est un processus gaussien.
Lien avec les équations aux dérivées partielles
Équation de Fokker-Planck
Généralisations
Il existe de multiples généralisations de la notion des EDS que nous venons de présenter :
- EDS avec des sauts ;
- EDS dirigées par d'autres types de processus, comme des mouvements browniens fractionnaires par exemple ;
- EDS en dimension infinie (à rapprocher des équations aux dérivées partielles stochastiques)
- ...
Domaines d'applications
- modélisation de phénomènes de diffusion en physique (mécanique des fluides, géophysique, ...) : c'est à l'origine de la motivation de l'étude du mouvement brownien ;
- dynamique des populations, écologie, ... : modélisation de la localisation de la population d'une espèce donnée, ou encore de sa taille...
- méthodes de Monte-Carlo : résolution de certaines équations aux dérivées partielles par des méthodes aléatoires ;
- mathématiques financières : modélisation des cours de bourse ;
- théorie du contrôle stochastique : il s'agit de trouver des stratégies permettant de minimiser ou maximiser certaines quantités soumises à des fluctuations aléatoires mais spécifiées par des paramètres que l'on peut faire varier (valeur d'un portefeuille d'actions, régulation du débit d'un barrage, ...) ;
- résonance stochastique, modélisation en neuroscience, climatologie (des modèles de climat sur de très longues périodes utilisent des EDS).
- modèles d'écoulements de polymères multi-échelles
Références et ouvrages
- C. G. Gardiner, Handbook of Stochastic Methods (3me d.), Springer, 2004. ISBN 3-540-20882-8
- I. Karatzas et S. Shreve, Brownian Motion and Stochastic Calculus, Graduate Texts in Mathematics (2me d.), Springer, 2004. ISBN 0-387-97655-8.
- E. Nelson, Dynamical Theories of Brownian Motion. Princeton University Press, 1967. Version PDF sur la page de l'auteur.
- B. Øksendal, Stochastic Differential Equations: An Introduction With Applications (6me d.), Springer, 2005. ISBN 3-540-04758-1
- D. Revuz et M. Yor, Continuous Martingales and Brownian Motion, (3me d.), Springer, 2004.ISBN 3-540-64325-7
- L.C.G. Rogers et D. Williams, Diffusions, Markov processes and martingales (2me d.), Cambridge Mathematical Library, Cambridge University Press, 2000. ISBN 0-521-77593-0
Simulation
- P. Kloeden et E. Platen, Numerical Solution of Stochastic Differential Equations, Springer, 2000. ISBN 3-540-54062-8
- P. Kloeden, E. Platen et H. Schurz, Numerical Solution of SDE Through Computer Experiments, Universitext, Springer, 2003. ISBN 3-540-57074-8
- B. Lapeyre, E. Pardoux et R. Sentis, Méthodes de Monte-Carlo pour les équations de transport et de diffusion, Springer, 1998. ISBN 3-540-63393-6
Liens externes
- (en) Liste d'EDS usuelles
- Portail des mathématiques
Catégories : Probabilités | Physique statistique | Processus stochastique | Méthode mathématique de la physique
Wikimedia Foundation. 2010.
