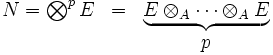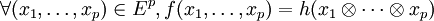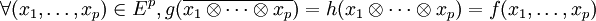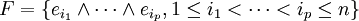Puissance exterieure

Puissance extérieure

La puissance extérieure p-ième d'un module E (sur un anneau commutatif) est une construction en algèbre extérieure qui est une solution au problème suivant : existe-t-il un module M, le « plus petit » possible et une application canonique φ : E^p → M telle que pour toute application multilinéaire alternée f définie sur E^p à valeur dans un module F quelconque, il existe une unique application g définie sur M à valeurs dans F telle que $f = g \circ \varphi$ ?

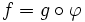Construction du produit extérieur

On considère le produit tensoriel :

$\begin{matrix} N = \bigotimes^p E & = & \underbrace{E \otimes_A \cdots \otimes_A E} \\ & & p \end{matrix}$

On sait que toute application multilinéaire 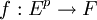$f : E^p \to F$ est en correspondance avec une application linéaire 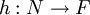$h : N \to F$ telle que :

$\forall (x_1, \dots, x_p) \in E^p, f(x_1, \dots, x_p) = h(x_1 \otimes \cdots \otimes x_p)$

Comme f est alternée, l'application h s'annule en tous les tenseurs décomposables 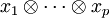$x_1 \otimes \cdots \otimes x_p$ tels qu'il existe i,j deux indices différents vérifiant x_i = x_j. Considérons le sous-module C de N engendré par les tenseurs de cette forme. Comme C est incluse dans le noyau de h, il existe une unique application multilinéaire g du module quotient N/C telle que :

$\forall (x_1, \dots, x_p) \in E^p, g(\overline{x_1 \otimes \cdots \otimes x_p}) = h(x_1 \otimes \cdots \otimes x_p) = f(x_1, \dots,x_p)$

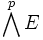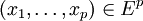On appelle donc puissance extérieur le quotient N/C et on le note $\bigwedge^p E$. Si $(x_1, \dots, x_p) \in E^p$, la classe de l'élément 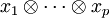$x_1 \otimes \cdots \otimes x_p$ se note 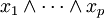$x_1 \wedge \cdots \wedge x_p$ (au lieu de 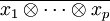$\overline{x_1 \otimes \cdots \otimes x_p}$ comme écrit précédemment).

Rang, dimension d'un produit extérieur

Lorsque E est un module libre de type fini sur un anneau commutatif A, il possède une base finie $(e_1, \dots e_n)$ et la famille suivante :

$F = \{e_{i_1} \wedge \cdots \wedge e_{i_p}, 1 \leq i_1 < \cdots < i_p \leq n\}$

est une base du produit extérieur $\bigwedge^p E$.

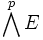En particulier, on déduit le résultat surprenant suivant : deux bases finies (e_i) et (f_j) d'un module sur un anneau commutatif ont même cardinal. En effet, soit n le cardinal de l'une, et m le cardinal de l'autre. Supposons n < m. Le produit extérieur 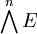$\bigwedge^n E$ est vide, car en utilisant la propriété précédente, on déduit que la famille vide est une base de 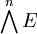$\bigwedge^n E$, par ailleurs, la famille 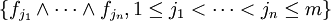$\{f_{j_1} \wedge \cdots \wedge f_{j_n}, 1 \leq j_1 < \cdots < j_n \leq m\}$ qui est non vide est également une base. D'où la contradiction, donc 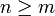$n \geq m$, par symétrie on déduit 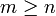$m \geq n$, d'où n = m.

Ce document provient de « Puissance ext%C3%A9rieure ».