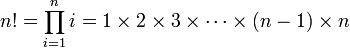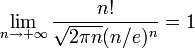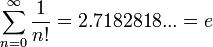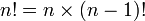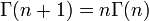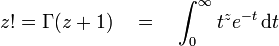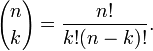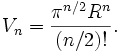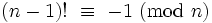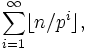0!

Factorielle

En mathématiques, la factorielle d'un entier naturel n, notée n!, ce qui se lit soit « factorielle de n » soit « factorielle n », est le produit des nombres entiers strictement positifs inférieurs ou égaux à n. La notation n! a été introduite en 1808 par Christian Kramp.

La factorielle joue un rôle important en algèbre combinatoire parce qu'il y a n! façons différentes de permuter n objets. Elle apparaît dans de nombreuses formules en mathématiques, comme par exemple la formule du binôme et la formule de Taylor.

Définition

n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5 040
8	40 320
9	362 880
10	3 628 800
11	39 916 800
12	479 001 600
13	6 227 020 800

Soit n un entier naturel. Sa factorielle est formellement définie par :

$n! = \prod_{i=1}^n i = 1\times 2\times 3\times \cdots \times (n-1) \times n$

Le tableau de droite donne les premières factorielles ; par exemple, on a

• 1! = 1
• 2! = 1 × 2 = 2
• 3! = 1 × 2 × 3 = 6
• 4! = 1 × 2 × 3 × 4 = 24
• 10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 3 628 800

Par convention :

0! = 1

La définition de la factorielle sous forme de produit rend naturelle cette convention puisque 0! est un produit vide, c'est-à-dire réduit à l'élément neutre de la multiplication. Cette convention est pratique pour plusieurs autres raisons :

• Elle permet une définition récursive de la factorielle : (n+1)! = n! × (n+1) pour tout n.
• Elle permet à des formules de dénombrement obtenues en analyse combinatoire d'être encore valides pour des tailles nulles. En particulier, le nombre d'arrangements ou de permutations de l'ensemble vide est égal à 1.
• La fonction Gamma (définie plus bas) permet alors d'écrire Γ(n + 1) = n! pour tout n.

La formule de Stirling donne un équivalent de n! quand n est grand :

$\lim_{n\to+\infty} \frac{n!}{\sqrt{2\pi n} (n/e)^n}=1$

d'où $n\,! \sim \sqrt{2\pi n}\, {\left(\frac n e\right)}^n$

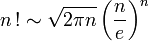
La somme des inverses des factorielles donne un nombre très connu des mathématiciens, la constante e.

$\sum_{n=0}^{\infty} \frac{1}{n!} = 2.7182818... = e$

Généralisation

Article détaillé : Fonction Gamma d'Euler.

La fonction gamma, tracée ici le long de l'axe des réels, prolonge la factorielle sur les valeurs qui ne sont pas entières

La fonction factorielle peut être prolongée à l'ensemble des nombres complexes (à l'exception des nombres entiers négatifs ou nuls) grâce à la fonction gamma d'Euler (notée Γ). En effet, pour n entier positif, on a :

Γ(n + 1) = n!

Par ailleurs, les deux fonctions satisfont les relations de récurrence suivantes :

$n!=n \times (n-1)!$

$\Gamma(n+1)=n \Gamma(n)~$

La fonction gamma agit donc comme un prolongement de la factorielle :

$z! = \Gamma(z+1)\quad = \quad \int_{0}^{\infty} t^z e^{-t}\, \mathrm{d}t\,\!$

Cette fonction n'est cependant pas définie pour les nombres entiers négatifs ou nuls (0, -1, -2, etc.).

Cette vision de la fonction gamma comme prolongation de la factorielle est justifiée par les raisons suivantes :

• les deux fonctions partagent une même définition récurrente ;
• la fonction gamma est généralement utilisée dans un contexte similaire (même si plus général) à la factorielle ;
• la fonction gamma est la seule fonction qui satisfait cette définition de récurrence sur les nombres complexes, qui est holomorphe et dont le logarithme de la restriction aux réels positifs est convexe (théorème de Bohr-Mollerup).

Exemples d'applications

• En combinatoire, il existe n! façons différentes d'arranger n objets distincts (c’est-à-dire n! permutations). Et le nombre de façons de choisir k éléments parmi un ensemble de n est donné par le coefficient binomial :

${n\choose k}={n!\over k!(n-k)!}.$

• En permutation, si r éléments peuvent être choisis et arrangés de r façons différentes parmi un total de n objets (r < n), alors le nombre total de permutations distinctes est donné par :

_nP_r = $\frac{n!}{(n-r)!}$

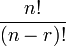
• Les factorielles apparaissent également en analyse. Par exemple, le théorème de Taylor, qui exprime la valeur en x d'une fonction f sous forme de série entière, fait intervenir la factorielle n! pour le terme correspondant à la n^e dérivée de f en x.

• Le volume d'une hypersphère en n dimensions peut être exprimé par :

$V_n={\pi^{n/2}R^n\over (n/2)!}.$

• Les factorielles sont utilisées de façon intensive en théorie des probabilités.

• Les factorielles sont souvent utilisées comme exemple — avec la suite de Fibonacci — pour l'apprentissage de la récursivité en informatique du fait de leur définition récurrente simple.

Théorie des nombres

Les factorielles ont de nombreuses applications en théorie des nombres. Les nombres factoriels sont des nombres hautement composés. En particulier, n! est divisible par tous les nombres premiers qui lui sont égaux ou inférieurs. Par conséquent, tout nombre n > 4 est un nombre composé si et seulement si :

$(n-1)!\ \equiv\ 0 \ ({\rm mod}\ n)$.

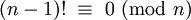Un résultat plus fort est le théorème de Wilson. n est premier si et seulement si :

$(n-1)!\ \equiv\ -1 \ ({\rm mod}\ n)$

Adrien-Marie Legendre a montré que la multiplicité du nombre premier p dans la décomposition en produit de facteurs premiers de n! peut être exprimé par :

$\sum_{i=1}^{\infty} \lfloor n/p^i \rfloor,$

(qui est définie, car la fonction partie entière élimine tous les pⁱ > n).

La seule factorielle qui soit également un nombre premier est 2, mais il existe des nombres premiers de la forme 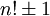$n! \pm 1$, appelés nombres premiers factoriels.

Variantes

Article détaillé : Analogues de la factorielle.

De nombreux auteurs ont défini des fonctions analogues, croissant plus rapidement encore, ainsi que des produits restreints à certains entiers seulement. On rencontre ainsi dans la littérature^[1] les fonctions primorielles, multifactorielles, superfactorielles, hyperfactorielles, etc. Mais il ne semble pas que, contrairement à la factorielle, omniprésente dans la plupart des branches des mathématiques, ces autres fonctions aient eu beaucoup d'applications autres que récréatives ; quant à leur utilisation pour désigner de très grands nombres, les notations de Knuth et celles de Conway s'avèrent à la fois plus maniables et beaucoup plus efficaces.

Notes et références

1. ↑ En particulier dans l'OEIS

Annexes

Articles connexes

• Fonction digamma
• Fonction gamma
• Nombre premier factoriel
• Primorielle

Liens externes

• (fr) <factorielle n!>
• (en) Fast Factorial Functions

Ce document provient de « Factorielle#D.C3.A9finition ».