- Polymere
-
Polymère
Polymère est un mot qui vient du grec « pollus » plusieurs, et « meros » partie.
Un polymère est une macromolécule, organique ou inorganique, constituée de l'enchaînement répété d'un même motif, le monomère (du grec monos : un seul ou une seule, et meros ; partie), reliés les uns aux autres par des liaisons covalentes.
Un corps formé de polymères peut se présenter sous forme liquide ou solide à température ambiante.
Un polymère peut être naturel (exemple : polysaccharides, ADN), obtenu par modification chimique d'un polymère naturel (exemple : méthylcellulose), ou bien entièrement synthétisé par voie chimique (ex.: polystyrène, polyisoprène) par une réaction de polymérisation.
L'enchaînement des monomères peut se faire de façon linéaire (polymères linéaires), présenter des ramifications aléatoires (polymères branchés) ou systématiques et régulières (dendrimères).
Du fait des degrés de liberté de la conformation de chaque monomère, la conformation tridimensionnelle du polymère résulte de cet enchaînement mais également des interactions entre monomères.
Sommaire
Généralités
Les polymères peuvent être fabriqués à partir d'un seul type de monomère (on parle alors d'homopolymère, comme par exemple le polystyrène); ou bien à partir de plusieurs types de monomères (on parle alors de copolymères, comme par exemple l'acrylonitrile butadiène styrène).
On distingue deux grandes catégories de réactions chimiques permettant la préparation des polymères : la polymérisation en chaîne ou polyaddition (pour produire par exemple le polyéthylène, le polystyrène, le polypropylène...) et la polymérisation par étapes ou polycondensation (pour produire par exemple le PET ou poly(éthylène téréphtalate)).
Les polymères sont souvent classés d'après leurs propriétés thermomécaniques. Citons notamment :
- les thermoplastiques, qui deviennent malléables quand ils sont chauffés ce qui permet leur mise en œuvre ;
- les thermodurcissables, qui durcissent sous l'action de la chaleur ou par ajout d'un additif ;
- les élastomères, qui sont déformables de manière réversible.
Les polymères sont devenus l'élément essentiel d'un nombre très important d'objets, dans lesquels ils ont souvent remplacé les substances naturelles. Le terme désigne des matières abondantes et variées : des protéines les plus ténues aux fibres de kevlar haute résistance. Certains polymères sont utilisés en solution comme par exemple dans les shampooings ; d'autres forment des matériaux solides. Pour ces applications, les polymères sont généralement mélangés à d'autres substances - des charges telles que la silice, des additifs tels que les antioxydants - dans des opérations de formulation. La fabrication des objets eux-mêmes résulte la plupart du temps d'une opération de mise en œuvre dans un procédé industriel qui relève du domaine de la plasturgie.
La description des polymères en tant qu'objet physique permettant de comprendre leurs propriétés relève de la physique statistique.
Historique
La notion de macromolécule n'est apparue que tardivement dans l'histoire de la chimie. Bien que présagée par Wilhelm Eduard Weber ou encore Henri Braconnot au début du XIXe siècle, de nombreux chercheurs ne voient là que des agrégats ou micelles. Il faut attendre les années 1920-1930 pour que l'idée de macromolécule soit acceptée, notamment grâce aux travaux d'Hermann Staudinger.
Le développement industriel consécutif de la science macromoléculaire a été accéléré ensuite par la Seconde Guerre mondiale. Les États-Unis d'Amérique ont été privés lors de leur entrée en guerre de leur approvisionnement en caoutchouc naturel en provenance d'Asie du Sud-Est. Ils ont alors lancé un immense programme de recherche visant à trouver des substituts de synthèse.
Structure et conformation
Séquence primaire
Les polymères sont des macromolécules, résultant de l'enchaînement covalent (voir liaison covalente) de "motifs de répétition" identiques ou différents les uns des autres. La masse molaire de ces molécules dépasse souvent 10 000 g/mol. Les liaisons covalentes constituant le squelette macromoléculaire sont le plus souvent des liaisons carbone-carbone (cas du polyéthylène, du polypropylène...), mais peuvent également résulter de la liaison d'atomes de carbone avec d'autres atomes, notamment l'oxygène (cas des polyéthers et des polyesters) ou l'azote (cas des polyamides). Il existe aussi des polymères pour lesquels l'enchaînement résulte de liaisons ne comportant pas d'atomes de carbone (polysilanes, polysiloxanes, etc...)
Cet enchaînement de motifs répétés présente chez les polymères les plus simples une structure linéaire, un peu comme un collier de perles. On peut également rencontrer des branches latérales (elles mêmes plus ou moins branchées), résultant soit d'une réaction chimique parasite au cours de la synthèse du polymère (par exemple dans le cas du polyéthylène basse densité ou PEBD), soit d'une réaction de greffage pratiquée volontairement sur le polymère pour en modifier les propriétés physico-chimiques.
Dans le cas où la macromolécule est composée de la répétition d'un seul motif – ce qui résulte le plus souvent de la polymérisation d'un seul type de monomère -, on parle d'homopolymères. Quand plusieurs motifs différents sont répétés, on parle de copolymères. On distingue ensuite plusieurs types de copolymères suivant l'organisation entre les différents monomères. Dans le cas le plus fréquent, on a un copolymère statistique où les différents monomères se mélangent en fonction de la réactivité et de la concentration de ceux-ci. Les propriétés mécaniques sont alors moyennées. En revanche, dans un copolymère séquencé ( l'anglicisme copolymère à blocs est parfois utilisé) ou copolymère alterné, il peut y avoir combinaison des propriétés mécaniques.

Il existe parfois des liaisons covalentes vers d'autres morceaux de chaînes polymères. On parle alors de molécules "branchées" ou ramifiées. On sait synthétiser par exemple des molécules en 'peigne' ou en 'étoile'. Lorsque de nombreuses chaînes ou chaînons ont été réunis par un certain nombre de liaisons covalentes, elles ne forment plus qu'une macromolécule gigantesque ; on parle alors de réseau macromoléculaire ou de gel.
Polymères linéaires
Lors de la réaction de polymérisation, lorsque chaque monomère est susceptible de se lier à deux autres, la réaction produit une chaîne linéaire. Typiquement, ce cas est celui des polymères dit "thermoplastiques".
Du fait des degrés de liberté de la conformation de chaque monomère, la façon dont la chaîne occupe l'espace n'est cependant pas rectiligne.
Notion de maillon statistique
Chaque monomère présente une certaine rigidité. Souvent, cette rigidité influence l'orientation du monomère voisin. Toutefois, cette influence s'estompe au fur et à mesure que l'on s'éloigne du monomère initial et finit par disparaître au-delà d'une distance l0, dite longueur d'un maillon statistique de la chaîne. Techniquement, cette longueur est la longueur de corrélation de l'orientation d'un maillon. Elle se nomme longueur de persistance du polymère.
Ayant introduit cette notion, il est alors possible de renormaliser la chaîne en considérant maintenant le maillon statistique comme son motif élémentaire. Pour décrire la conformation de cette chaîne, les particularités propres à la structure chimique du monomère n'interviennent plus.
Chaîne idéale (ou gaussienne)
Le cas le plus simple est celui de l'enchaînement linéaire de maillons n'exerçant pas d'interaction entre-eux. À l'état liquide, la chaîne adopte dans l'espace une conformation qui pour une molécule donnée change sans cesse du fait de l'agitation thermique. À l'état de solide amorphe ou à un instant donné dans le cas d'un liquide, la conformation des chaînes est différente d'une molécule à l'autre. Cette conformation obéit néanmoins à des lois statistiques.
Soit dans la séquence primaire de la chaîne un maillon donné pris pour origine. Lorsque les maillons n'interagissent pas, la probabilité que le nieme maillon de la chaîne soit à une distance r de l'origine obéit à une loi normale ou loi Gaussienne de moyenne nulle et de variance n. Une longueur caractéristique de la chaîne est la distance R entre ses deux extrémités (dite "distance bout-à-bout"). La moyenne arithmétique de R est nulle. Ainsi, pour caractériser la taille de la pelote que forme la chaîne, il faut considérer la moyenne quadratique, notée ici
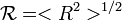 . En raison de la loi normale, cette moyenne varie comme la racine carré du nombre N de maillons.
. En raison de la loi normale, cette moyenne varie comme la racine carré du nombre N de maillons.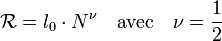
La conformation statistique d'une telle chaîne est l'analogue de la trace laissée par un marcheur aléatoire où N représente le nombre de pas de la marche, l0 leur longueur et
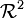 le déplacement carré moyen du marcheur.
le déplacement carré moyen du marcheur.Dans les années 70, Pierre-Gilles de Gennes a montré l'analogie entre la description d'une chaîne polymère et les phénomènes critiques. Aussi, l'utilisation de la lettre ν pour désigner l'exposant, obéit à la nomenclature des exposants critiques. Les objets rencontrés dans les phénomènes critiques ont des propriétés d'autosimilarité et peuvent être décrit en termes de géométrie des fractals, dans ce cas l'exposant ν représente l'inverse de la dimension fractale df:
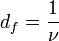
Une conformation gaussienne des chaînes se rencontrent dans deux cas :
- Lorsque les chaînes sont nombreuses et entremêlées (pensez à un plat de spaghetti). Un maillon donné est alors entouré indifféremment par les maillons de la chaîne à laquelle il appartient et par les maillons des chaînes voisines. Les interactions des uns et des autres avec ce maillon se compensent exactement.
- Lorsqu'une chaîne est seule à une température particulière appelée température-θ à laquelle les forces attractives de van der Waals entre deux maillons sont exactement compensées par les forces répulsives dites de volume exclu (cette force répulsive provient du fait que deux maillons ne peuvent physiquement être en même temps au même endroit).
Chaîne gonflée (ou à "volume exclu")
Lorsque les interactions répulsives entre maillons d'une même chaîne dominent (typiquement à température plus haute que la température-θ), la conformation de la chaîne s'en trouve "gonflée" par rapport à sa conformation idéale. Dans ce cas la valeur de l'exposant ν et la taille caractéristique de la pelote que forme la chaîne sont supérieures à celle d'une chaîne idéale :
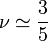
La valeur approchée de cet exposant fut établie par Paul Flory dans les années 40. Bien qu'il ait été démontré depuis que le raisonnement utilisé à l'époque était erroné, la valeur 3 / 5 est étonnamment proche de la valeur exacte
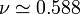 trouvée depuis par les méthodes beaucoup plus sophistiquées du groupe de renormalisation.
trouvée depuis par les méthodes beaucoup plus sophistiquées du groupe de renormalisation.En termes de marche aléatoire, une chaîne gonflée correspond à la trace laissée par un marcheur effectuant une marche aléatoire autoévitante.
Chaîne globulaire
Lorsque les interactions attractives entre maillons d'une même chaîne dominent (typiquement à température plus basse que la température-θ), la chaîne s'effondre sur elle-même et adopte une conformation compacte dite "globulaire" (à opposer au terme "pelote" utilisé pour les conformations idéale ou gonflée). Dans ce cas :
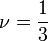
Le terme « conformation compacte » se comprend mieux en écrivant la relation « taille caractéristique-nombre de maillons » sous la forme :
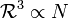 , qui exprime que le volume du globule est proportionnel au nombre de maillons. Ce comportement est celui d'un objet homogène dont la masse volumique est une constante indépendante de sa taille.
, qui exprime que le volume du globule est proportionnel au nombre de maillons. Ce comportement est celui d'un objet homogène dont la masse volumique est une constante indépendante de sa taille.Polymères en solution
Implicitement nous avons considéré jusqu'ici une chaîne seule dont les maillons seraient comme les molécules d'un gaz. Dans la pratique, les chaînes sont soit en présence de leurs semblables, très proches les unes des autres et entremêlées (cas évoqué au paragraphe "chaîne gaussienne"), soit en présence d'un solvant. Ce dernier cas est celui d'une solution de polymère.
En solution, la conformation du polymère résulte du bilan des interactions "monomère-monomère", "monomère-solvant" et "solvant-solvant". Il est possible de rendre compte de ce bilan au moyen d'un paramètre effectif d'interaction, appelé paramètre de Flory-Huggins. Trois cas sont envisageables :
- Bon solvant : le couple polymère-solvant est tel qu'un monomère minimise son énergie libre lorsqu'il est entouré de molécules de solvant. Les interactions effectives entre maillons de la chaîne sont donc répulsives, favorisant ainsi la dispersion des polymères et leur solubilisation (d'où le terme "bon solvant"). C'est le cas d'un polymère dans un solvant constitué de monomères, par exemple le polystyrène en solution dans le styrène.
- Solvant-θ: le bilan des interactions entre maillons de la chaîne est nul. Ce cas se rencontre à une température précise (température-θ) qui n'est pas toujours accessible expérimentalement. Lorsque cette température est accessible, le solvant est qualifié de θ. Par exemple, le cyclohexane est un solvant-θ du polystyrène à 35 °C.
- Mauvais solvant : les interactions effectives entre maillons de la chaîne sont attractives. Dans ce cas, la solubilisation (dispersion) des polymères n'est pas directement réalisable, elle peut se faire à température suffisamment élevée pour que le solvant soit "bon". En refroidissant, les polymères peuvent se trouver en mauvais solvant mais rester dispersés si la solution est suffisamment diluée. Ce cas peut également se rencontrer pour des polymères séquencés dont l'une des séquences (majoritaire) serait en situation de bon solvant, permettant ainsi la solubilisation et forçant une autre séquence à se trouver en situation de mauvais solvant.
En solution suffisamment diluée, les chaînes sont bien séparées les unes des autres. La conformation d'une chaîne ne dépend alors que du bilan des interactions effectives entre ses propres maillons. En solvant-θ, la conformation est idéale (ν = 1 / 2), en bon solvant elle est gonflée (
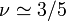 ) et en mauvais solvant elle est globulaire (ν = 1 / 3).
) et en mauvais solvant elle est globulaire (ν = 1 / 3).Polymères branchés et transition sol-gel
Certaines molécules ont la propriété de pouvoir se lier aléatoirement à au moins trois autres durant leur réaction de polymérisation. Les polymères qui en résultent ne sont plus linéaires mais branchés et réticulés et leur taille très largement distribuée. La moyenne de cette distribution augmente avec l'avancement de la réaction. L'ensemble de la population des molécules est soluble (on la désigne par le terme sol) jusqu'à ce que la molécule la plus grande soit de taille macroscopique et connecte les deux bords du récipient contenant le bain de réaction. Cette molécule est appelée le gel. Typiquement, ce type de réaction est à la base des résines thermodurcissables.
L'apparition du gel confère au bain de réaction, initialement liquide, une élasticité qui est la caractéristique d'un solide. Cette transition de phase est bien décrite par un modèle de percolation (conjecture émise en 1976 de façon indépendante par Pierre-Gilles de Gennes et Dietrich Stauffer et bien vérifiée expérimentalement depuis) qui prévoit la forme de la fonction de distribution, p(N), du nombre de monomères de chaque molécule et la façon dont elles occupent l'espace. Jusqu'à la molécule la plus grande, p(N) est une loi de puissance du type :
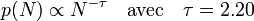
Un taille caractéristique,
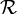 , de chaque molécule peut être définie par la moyenne quadratique des distances entre monomères, on parle de rayon de giration. La relation entre cette longueur et le nombre de monomères est également une loi de puissance :
, de chaque molécule peut être définie par la moyenne quadratique des distances entre monomères, on parle de rayon de giration. La relation entre cette longueur et le nombre de monomères est également une loi de puissance :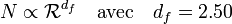
où df est la dimension fractale des molécules. Les valeurs particulières de ces exposants font qu'ils obéissent à la relation dite d'hyperéchelle reliant les exposants critiques à la dimension de l'espace d: d / df = τ − 1. L'implication majeure de cette relation est que les polymères branchés occupent l'espace à la façon des poupées russes, les petits à l'intérieur du volume occupé par les plus grands.
Aspects expérimentaux
Diffusion de rayonnement
Les caractéristiques structurales des polymères sont accessibles expérimentalement par des expériences de Diffusion élastique de rayonnement: diffusion de la lumière, diffusion aux petits angles des rayons X et des neutrons.
Ces expériences consistent à éclairer un échantillon par une onde plane, monochromatique, de vecteur d'onde
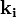 . Une partie de cette onde est déviée par les atomes constituants l'échantillon. Les ondes ainsi diffusées produisent des Interférences dont l'analyse peut fournir des renseignements sur certaines caractéristiques de l'échantillon.
. Une partie de cette onde est déviée par les atomes constituants l'échantillon. Les ondes ainsi diffusées produisent des Interférences dont l'analyse peut fournir des renseignements sur certaines caractéristiques de l'échantillon.L'intensité totale, I, de l'onde diffusée dans une certaine direction est recueillie à une distance D de l'échantillon. En toute généralité, on peut écrire :
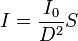
où I0 est l'intensité de l'onde incidente (exprimée en nombre de particules, photons ou neutrons selon le rayonnement, par unité de temps et de surface). La grandeur S, appelée section efficace différentielle de diffusion de l'échantillon, est homogène à une surface et contient l'information qui nous intéresse.
La diffusion élastique de rayonnement suppose que les ondes diffusées, de vecteur d'onde
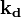 , sont de même longueur d'onde que l'onde incidente :
, sont de même longueur d'onde que l'onde incidente : 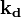 et
et 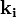 ont la même norme. La section efficace différentielle de diffusion est mesurée en fonction du vecteur de diffusion
ont la même norme. La section efficace différentielle de diffusion est mesurée en fonction du vecteur de diffusion 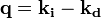 .
.Si l'échantillon est isotrope, la mesure ne dépend pas de l'orientation de
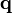 mais uniquement de sa norme qui s'écrit :
mais uniquement de sa norme qui s'écrit :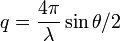
où λ est la longueur d'onde et θ l'angle de diffusion.
Solutions diluées de polymères : petites valeurs de q
Pour une solution suffisamment diluée de polymères, on peut montrer que la section efficace différentielle de diffusion s'écrit (cf. Diffusion élastique de rayonnement):
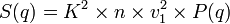
où n est le nombre de chaînes en solution, v1 le volume de chacune d'elles (c'est à dire la somme des volumes de tous ses monomères et non pas le volume de la sphère contenant la pelote), et K2 un facteur représentant le contraste entre le polymère et le solvant et qui dépend du rayonnement utilisé. Ce facteur de contraste peut se mesurer où se calculer à partir de données tabulées : c'est une grandeur connue dans la plupart des cas.
La grandeur P(q) est appelée facteur de forme des polymères en solution. C'est une grandeur normalisée telle que P(0) = 1. Pour une chaîne polymère de N maillons de masse molaire m0 et de masse volumique ρ, l'équation précédente devient :
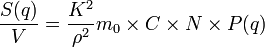
où C = nNm0 / V est la concentration de la solution exprimée en masse par unité de volume (g/cm3 par exemple).
On peut montrer (voir Diffusion élastique de rayonnement), qu'à petit vecteur de diffusion comparé à la taille moyenne des pelotes, la section efficace par unité de volume s'écrit :
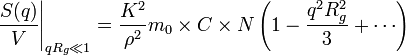
Rg est une grandeur caractéristique de la taille moyenne des pelotes que forment les chaînes. Cette grandeur appelée "rayon de giration" est la moyenne quadratique des distances des monomères au centre de gravité de chaque pelote.
Pour une solution très diluée, de concentration C connue et pour un rapport K2 / ρ2m0 également connu : la grandeur mesurée, S(q), varie de façon affine avec le carré q2 du vecteur de diffusion. L'ordonnée à l'origine permet de déterminer le nombre N de maillons des chaînes en solution. La pente de la droite permet de déterminer le rayon de giration Rg. C'est ce type d'expériences qui à permis de vérifier les relations entre ces deux grandeurs et de déterminer en particulier l'exposant ν = 1 / df qui les unit.
Solutions diluées de polymères : loi d'échelle
Les objets ordinaires ont une masset, M, qui varie comme la puissance 1, 2 ou 3 de leur taille R. Pour les objets fractals, cette puissance n'est pas nécessairement entière :
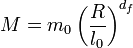
df est la dimension fractale de cette famille d'objets. Elle caractérise la façon dont ils remplissent l'espace. Les fractals sont le plus souvent autosimilaires, c'est à dire invariant par changement d'échelle. Une fois grossie, une petite partie est statistiquement semblable à l'objet entier. Observons sous différents grossissements la pelote que forme une chaîne polymère de rayon de giration Rg. Si
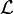 est la taille de la zone observable, pour
est la taille de la zone observable, pour 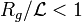 (petit grossissement), la masse visible, m, est égale à la masse totale M. Par contre pour
(petit grossissement), la masse visible, m, est égale à la masse totale M. Par contre pour 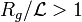 (fort grossissement) la masse visible décroît lorsque le grossissement augmente. Supposons une loi du type :
(fort grossissement) la masse visible décroît lorsque le grossissement augmente. Supposons une loi du type :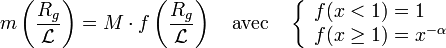
Pour déterminer l'exposant α, on utilise un argument d'échelle qui postule [1]:
- qu'une seule longueur est pertinente pour décrire l'objet (ici son rayon Rg).
- qu'à fort grossissement, la mesure est insensible à M (on ne peut déduire la masse totale de l'objet en n'observant qu'une partie). Ce qui s'exprime par
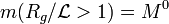 .
.
La relation précédente donne α = df.
C'est ce qui se passe lors d'une expérience de diffusion de rayonnement pour laquelle l'échelle d'observation peut être assimilée à l'inverse du vecteur de diffusion :
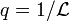 . En solution très diluée, la grandeur physique donnant accès à la masse d'un objet est la section efficace de diffusion cohérente par unité de volume, de concentration et de contraste :
. En solution très diluée, la grandeur physique donnant accès à la masse d'un objet est la section efficace de diffusion cohérente par unité de volume, de concentration et de contraste :![\left[{S(q)/(VCK^2)}\right]_{C\to 0}=M\times P(qR_g)=m(qR_g)](/pictures/frwiki/51/3ff53b387a5056c8bc9ecfac5658088b.png)
Dans le régime intermédiaire du vecteur de diffusion tel que Rg < q − 1 < l0, la mesure sonde l'intérieur de l'objet et est sensible à son autosimilarité. L'argument d'échelle postule qu'une seule longueur est pertinente (or Rg est déjà nécessaire à qRg < 1) et que l'expérience est insensible à M. Soit :
![\begin{array}{rl}
\left[{S(q)/(CVK^2)}\right]_{C\to 0}=M\times P(qR_g)
&\textrm{avec}\quad\left\{{
\begin{array}{l}
P(qR_g<1)=1\\
P(qR_g\ge 1)=(qR_g)^{-d_f}
\end{array}}\right.
\end{array}](/pictures/frwiki/49/15bfcb9ec7a60b96a191644939ea2b3d.png)
Une expérience de diffusion de rayonnement réalisée à grand vecteur de diffusion par rapport au rayon de giration des chaînes donne directement accès à la dimension fractale des chaînes en solution. Cette façon de déterminer df utilise l'autosimilarité d'une chaîne seule, tandis que la précédente basée sur des mesures à petit vecteur de diffusion utilise l'autosimilarité des chaînes entre elles.
Chromatographie d'exclusion stérique
Chromatographie d'exclusion stérique
Procédés de mise en œuvre
Il existe plusieurs méthodes pour mettre en forme un produit à partir du polymère :
- l'extrusion : filières...
- l'extrusion-soufflage : films...
- l'injection: très grande variétés de pièces
- l'injection-soufflage
- le rotomoulage : pièce fermée, pouvant être de très grandes dimensions
- le thermoformage : baignoires...
Nomenclature
La nomenclature UICPA recommande de partir du motif de base de la répétition. Cependant de très nombreux polymères ont des noms usuels ne respectant pas cette nomenclature, mais sont basés sur le nom des molécules servant à synthétiser le polymère. Un exemple : Le polymère de formule (CH2 − CH2)n est couramment appelé polyéthylène (PE) . Pour respecter la nomenclature UICPA, il devrait être nommé "polyméthylène" car le motif constitutif n'est pas l'éthylène CH2 = CH2 mais le méthylène CH2.
Voici quelques autres exemples de cas où l'appellation usuelle et la nomenclature UICPA diffèrent :
Formule Nom UICPA Appellation usuelle (O − CH2 − CH2)n Poly(oxyéthylène) Polyoxyde d'éthylène (O − CH2)n Poly(oxyméthylène) Polyformaldéhyde (CH2 − CH = CH − CH2)n Poly(1-buténylène) Polybutadiène Exemples
- Polymères naturels :
- Polymères industriels :
- Le polyamide (PA)
- Le polyimide (PI)
- Le polycarbonate (PC)
- Le chlorure de polyvinyle (PVC)
- Le polyéthylène (PE)
- Le polyéthylène téréphtalate (PET)
- Le polyéthylène naphtalate (PEN)
- Le polyméthacrylate de méthyle (PMMA)
- Le polypropylène (PP)
- Le polystyrène (PS)
- Le polytétrafluoroéthylène (PTFE), plus connu avec le nom de teflon
- Le polyuréthane (PU)
- Le polyfluorure de vinylidène ( PVDF)
- Le poly(diméthylsiloxane) (PDMS)
- Les polymères époxyde
Références
- ↑ P. G. de Gennes. Scaling concepts in polymer physics. Cornell Univ. Press, 1996.
Voir aussi
Bibliographie
- Polymers : Chemistry and Physics of Modern Materials, J-M. Cowie (Blackie, 1991) (ISBN 075140134X)
- De la macromolécule au matériau polymère, J-L. Halary, F. Lauprêtre, (Belin Echelles, 2004) (ISBN 2701134226)
- Mécanique des matériaux polymères, J-L. Halary, F. Lauprêtre, L.Monnerie, (Belin Echelles, 2008) (ISBN 2701145910)
Articles connexes
- Matière plastique
- Chimie
- Pétrochimie
- Peinture
- Oligomère
- Polymérisation
- Polymérisation radicalaire
- Polycondensation
Liens externes
- (fr) Abréviations de plus de 230 polymères industriels
- (fr) Polymère comme biomatériau osseux
- (fr) Nomenclature UIPAC des polymères traduit en français
- (en) Un jeu pour découvrir les polymères
- (en) Polymer & Plastics Glossary
- Portail de la chimie
- Portail de la physique
Catégorie : Polymère
Wikimedia Foundation. 2010.


