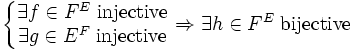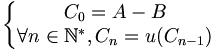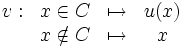- Theoreme de Cantor-Bernstein
-
Théorème de Cantor-Bernstein
Le théorème de Cantor-Bernstein, également appelé théorème de Cantor-Schröder-Bernstein, est un théorème de la théorie des ensembles. Il est nommé en l'honneur des mathématiciens Georg Cantor, Felix Bernstein et Ernst Schröder. Cantor en donna une première démonstration, mais qui utilisait implicitement l'axiome du choix. Bernstein et Schröder en donnèrent des démonstrations qui ne dépendaient pas de cet axiome.
Sommaire
Historique
Georg Cantor l'énonce dans son livre Sur les fondements de la théorie des ensembles transfinis mais ne le démontre pas. Felix Bernstein, élève de celui-ci en esquisse une démonstration dès 1896 à l'âge de 18 ans. Elle est publiée en 1898 sur proposition de Cantor dans Leçons sur la théorie des fonctions sous la plume d'Émile Borel. Ernst Schröder le démontre également dans un article daté de la même année, cette démonstration étant cependant considérée comme imparfaite[1].
Richard Dedekind en fit lui même une démonstration en 1897 mais qui ne fut publiée qu'en 1930. Ernst Zermelo en fait une autre en 1906 qui reprend en fait les idées de Dedekind
Énoncé
S'il existe une injection f d'un ensemble E vers un ensemble F, et une injection g de l'ensemble F vers l'ensemble E, alors il existe une bijection h de E sur F.
Démonstration n°1
Lemme préliminaire
Commençons par montrer que si u est une application injective d'un ensemble A vers un ensemble B avec
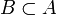 , alors il existe une bijection v de A sur B.
, alors il existe une bijection v de A sur B.Soit
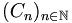 la suite définie par :
la suite définie par :Soit C la réunion de tous les ensembles
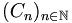 :
: 
Soit alors v l'application de A dans B défini par :
v est bien défini à valeurs dans B, car u est à valeur dans B, et si
 alors
alors 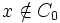 et donc
et donc 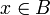 .
.Montrons que v est injective. Soient alors x et y deux éléments de A tel que v(x) = v(y)
-
-
- Supposons que
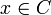 et
et 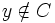 .
.
- Alors
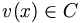 (car C est stable par v) et
(car C est stable par v) et 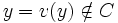 . Or v(x) = v(y) ce qui est absurde.
. Or v(x) = v(y) ce qui est absurde.
- Supposons que
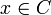 et
et 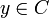 .
.
- Alors v(x) = u(x) = v(y) = u(y). Comme u est injective x = y.
- Supposons que
 et
et 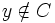 .
.
- Alors x = y = v(x) = v(y)
- Supposons que
- Dans tous les cas x = y, donc v est injective.
-
Montrons que v est surjective. Soit
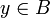 . Montrons qu'il existe un
. Montrons qu'il existe un 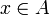 tel que v(x) = y.
tel que v(x) = y.-
-
- Si
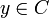
- alors il existe
 tel que
tel que 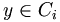 . (i est strictement positif car
. (i est strictement positif car 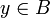 , donc
, donc  ).
). - Il existe donc
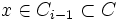 tel que u(x) = v(x) = y.
tel que u(x) = v(x) = y.
- Si
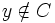
- alors v(y) = y
- Si
-
Donc v est bijective. Ce qui démontre la première proposition.
Interprétation
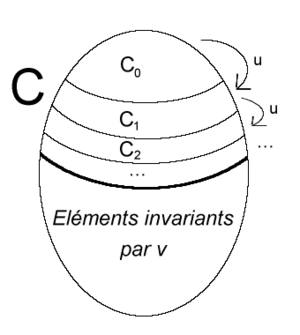
On peut donner une interprétation concrète du résultat montré ci-dessus. A est l'ensemble (infini !!) des spectateurs d'un théâtre (infini). Chaque spectateur a réservé une place, et initialement, on suppose que chaque place est occupée par un spectateur, mais pas forcément par le spectateur qui a réservé cette place. B est alors l'ensemble des spectateurs assis. Par ailleurs, les ensembles étant infinis, il peut rester des spectateurs debout. L'application u est l'application qui, à un spectateur x associe le spectateur y = u(x) assis à la place de x.
C0 est l'ensemble des spectateurs initialement debout. Ces spectateurs se rendent à leur place et délogent leur occupant. Ceux-ci forment alors l'ensemble C1. Ces derniers procèdent de même. Cn désigne les spectateurs debout à la n-ème étape. Ils vont aux places qu'ils ont réservé et en chassent leurs occupants. On itère une infinité de fois. C désigne l'ensemble des spectateurs qui se sont levés au moins une fois (y compris ceux qui étaient debout initialement).
L'application v désigne l'application, qui, à un spectateur x qui doit se lever, associe le spectateur y qu'il va déloger, ou bien qui, à un spectateur x qui reste toujours assis, associe x lui-même. L'application réciproque de v est l'application, qui, à un spectateur y qui est dérangé, associe le spectateur x qui vient prendre sa place, ou bien qui, à un spectateur y jamais dérangé, associe y lui-même.
Démonstration finale du théorème
Montrons alors le théorème initial.
Soit B = g(F) l'image de F par l'application g injective. L'application
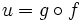 est une application injective de E dans B, avec
est une application injective de E dans B, avec 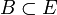 . Donc il existe une application bijective v de E sur B. Comme g est une injection, la restriction de g à son image pour espace d'arrivée est une bijection de F sur B. Donc la composée
. Donc il existe une application bijective v de E sur B. Comme g est une injection, la restriction de g à son image pour espace d'arrivée est une bijection de F sur B. Donc la composée 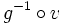 est une bijection de E sur F, ce qui démontre le théorème de Cantor-Bernstein.
est une bijection de E sur F, ce qui démontre le théorème de Cantor-Bernstein.Démonstration n°2
Un lemme préliminaire
Cette démonstration repose sur le lemme suivant, cas particulier du théorème de Knaster-Tarski. Soit E un ensemble et
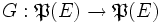 (où
(où  est l'ensemble des parties de E) une application croissante, i.e.
est l'ensemble des parties de E) une application croissante, i.e. 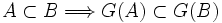 . Alors G admet un point fixe, i.e.
. Alors G admet un point fixe, i.e. 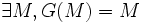 .
.En effet, posons
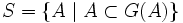 et
et 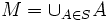 . Alors :
. Alors :- pour tout
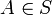 , d'une part
, d'une part  , d'autre part
, d'autre part 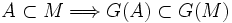 car G est croissante. Donc
car G est croissante. Donc 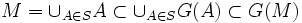 et donc
et donc 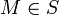 . M est donc la partie maximale de S
. M est donc la partie maximale de S
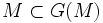 donc
donc 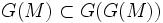 car G est croissante. Donc
car G est croissante. Donc 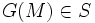 donc
donc 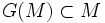 compte tenu de la maximalité de M comme élément de S. On a donc bien G(M) = M
compte tenu de la maximalité de M comme élément de S. On a donc bien G(M) = M
Démonstration finale
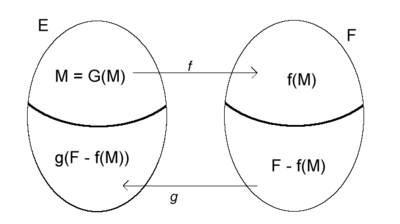
Soient maintenant f injective de E dans F et g injective de F dans E. Pour toute partie A de E, on pose G(A) = E − g(F − f(A)). On calcule f(A) ensemble des images des éléments de A par f, on en prend le complémentaire dans F, on prend l'ensemble g(F − f(A)) des images des éléments de cette partie par g et on prend le complémentaire dans E. Il n'est pas difficile de vérifier que G est croissante.
On introduit alors la partie M du lemme préliminaire. Cette partie est invariante par G ce qui signifie que g(F − f(M)) est exactement le complémentaire de M dans E.
On pose :
- si

- si
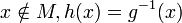
h est bijective de E dans F.
M joue un rôle comparable à la partie C dans la première démonstration ou à
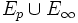 dans la démonstration qui suit.
dans la démonstration qui suit.Démonstration n° 3
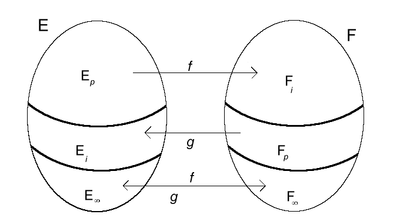
Appelons ancêtres d'un élément x de E l'antécédent de x par g (s'il existe) puis l'antécédent de cet antécédent par f, etc. Procédons de même pour les éléments de F.
Notons Ep (resp. Ei) l'ensemble des éléments de E ayant un nombre pair (resp. impair) d'ancêtres. Ep n'est autre que la partie C de la première démonstration. Notons
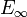 l'ensemble des éléments de E ayant un nombre infini d'ancêtres. Ep, Ei et
l'ensemble des éléments de E ayant un nombre infini d'ancêtres. Ep, Ei et 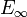 forment une partition de E. Définissons de même Fp, Fi et
forment une partition de E. Définissons de même Fp, Fi et 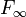 .
.f est une bijection de Ep sur Fi et aussi de
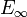 sur
sur 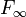 . g est une bijection de Fp sur Ei, et sa réciproque est donc une bijection de Ei sur Fp.
. g est une bijection de Fp sur Ei, et sa réciproque est donc une bijection de Ei sur Fp.On peut ainsi construire une bijection de E sur F.
Applications
Si l'on considère la technique naïve qu'a un enfant pour compter le nombre d'éléments d'un ensemble, cela revient quasiment toujours à associer chacun des élements à un autre d'un ensemble connu dont le nombre d'éléments est connu.
Il peut s'agir soit d'associer chacun des éléments à compter avec l'un des doigts, soit d'associer chacun des éléments avec un nombre que l'on réciterait à haute voix (un, deux, trois, etc.), par exemple.
En clair, compter se fait naïvement en effectuant une bijection d'un ensemble dont la « dimension » est connue vers un autre dont la dimension est inconnue.
Ce théorème s'interprète alors comme disant : « Si je peux compter une partie d'un ensemble avec la totalité des éléments d'un autre ensemble, et réciproquement, alors ils ont le même nombre d'éléments ». Ce qui est évident pour des ensembles finis. Ce théorème généralise alors cette notion pour des ensembles infinis.
- Si je peux compter un certain nombre de billes de mon sac de billes avec mes dix doigts, et qu'avec la totalité de mes billes, je peux les associer avec certains de mes doigts, alors j'ai exactement dix billes.
À partir de là, ce théorème représente l'une des briques de base pour généraliser la notion de tailles d'ensembles à des ensembles infinis.
Généralisation
Soient X un ensemble non vide et
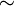 une relation d'équivalence sur l'ensemble des parties de X. On suppose qu'elle vérifie les deux propriétés:
une relation d'équivalence sur l'ensemble des parties de X. On suppose qu'elle vérifie les deux propriétés:- si
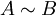 alors il existe une bijection f de A dans B telle que, pour tout sous-ensemble C de A,
alors il existe une bijection f de A dans B telle que, pour tout sous-ensemble C de A, 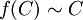 ;
; - si
 et
et  et
et 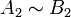 alors
alors 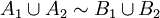 .
.
Soient deux ensembles A et B, un sous-ensemble A1 de A et un sous-ensemble B1 de B. On suppose que
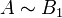 et
et 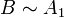 . Alors
. Alors 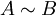 .
.Ceci peut également être démontré sans l'axiome du choix[2]. Dans le cas particulier où
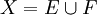 et
et  est la relation d'équipotence, on retrouve le résultat précédent.
est la relation d'équipotence, on retrouve le résultat précédent.Références
- Portail des mathématiques
Catégories : Théorie des ensembles | Théorème de mathématiques | Georg Cantor
Wikimedia Foundation. 2010.