- Logarithme Décimal
-
Logarithme décimal
Le logarithme décimal ou log10 est le logarithme de base dix. Il est défini en tous les réels strictement positifs x.
Le logarithme décimal est la fonction continue qui transforme un produit en somme et qui vaut 1 en 10.
Le logarithme décimal est la fonction réciproque de la fonction f(x)=10x
- pour x>0, si y = log10(x) alors x=10y.
Avant 1970, les calculatrices électroniques n'étaient pas encore d'un usage très répandu. Pour effectuer des produits ou des quotients, on utilisait encore des table de logarithmes de base 10 que l'on trouvait dans les appendices de beaucoup de livres, et les calculs étaient effectués à la main sur papier. Les logarithmes de base 10 ou logarithmes décimaux étaient appelés logarithmes vulgaires.
Les logarithmes vulgaires sont parfois appelés les logarithmes de Briggs. Henry Briggs fut un mathématicien britannique du XVe siècle, auteur des tables de logarithmes décimaux publiées à Londres en 1624 dans un traité intitulé Arithmetica Logarithmetica.
Sommaire
Mantisse et caractéristique
Les logarithmes des puissances entières de 10 se calculent aisément en utilisant la règle de conversion d'un produit en somme :
- log(10) = 1, log(100) = log(10 * 10) = log(10) + log(10) = 2, log(1000) = 3, log(10n) = n
- log(0,1) = log
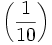 = - log(10) = -1, log(0,01) = - 2 , log(0,001) = -3
= - log(10) = -1, log(0,01) = - 2 , log(0,001) = -3
Les propriétés arithmétiques des logarithmes permettent de déduire la valeur de tout logarithme pourvu que soient connus les logarithmes de tous les nombres compris entre 1 et 10 (exclu). En effet, tout nombre x peut s'écrire sous la forme a.10n où a est un nombre compris entre 1 et 10 (exclu). Cette écriture s'appelle la notation scientifique de x. 10n représente alors l'ordre de grandeur du nombre x. Par exemple
- 120 = 1,2.102 et 0,00314 = 3,14.10 − 3
Le passage au logarithme décimal va alors mettre en évidence les deux éléments de l'écriture scientifique du nombre
- log(120) = log(1,2) + log(102) = log(1,2) + 2
- log(0,00314) = log(3,14) + log(10 − 3) = log(3,14) - 3
- log(x) = log(a.10^n) = n + log(a)
Puisque la fonction log est croissante, pour tout réel a compris entre 1 et 10 (exclu), log(a) est compris entre 0 et 1. L'entier relatif n est donc la partie entière de log(x) et log(a) la partie décimale à ajouter à n pour obtenir log(x).
La partie entière de log(x) est appelée la caractéristique du log.
La partie décimale à rajouter à la partie entière s'appelle la mantisse
On fera attention à l'écriture du logarithme des nombre plus petits que 1
- log(0,00314) = -3 + log(3,14)
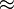 -3 + 0,497
-3 + 0,497 - log(0,00314)
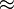 -2,503
-2,503
La deuxième écriture, qui semble plus naturelle, ne permet pas de retrouver rapidement la caractéristique (-3) et la mantisse (0,497). On préfère alors utiliser la première écriture que l'on note souvent
La lecture du logarithme d'un nombre permet alors aisément de déterminer son ordre de grandeur :
- si log(x) = 5,3
Sa caractéristique est 5 donc x est de la forme a.105. Sa mantisse est 0,3 qui est proche de log(2). donc x est proche de 2.105
Usage des logarithmes décimaux
Le développement des calculatrices de poche ont fait perdre aux logarithmes leur principal intérêt de simplification des calculs. Ils restent cependant très présents en physique quand il s'agit d'appréhender des quantités pouvant varier de 10 − 10 à 1010. C'est ainsi qu'on les retrouve dans le calcul des pH (potentiel hydrogène), des décibels, ...
Calculer avec une table de logarithmes
Article détaillé : table de logarithmes.L'idée directrice est de remplacer, pour l'utilisateur, les multiplications par des additions, les divisions par des soustractions, les puissances par des produits, les racines nièmes par des divisions par n.
Exemple 1 : En supposant que x = 435,728 et y = 1,6275 comment effectuer, sans calculatrice, le produit xy ?
- On calcule log(x)
- x = 4,35728.102 donc la caractéristique est 2, la mantisse se lit dans une table de logarithme : 0,6392
- log(x) = 2,6392
- on calcule log(y) , caractéristique 0, mantisse 0,2115
- log(y) = 0,2115
Il suffit de calculer log(xy) = log(x) + log(y) = 2,8507, d'isoler la caractéristique : 2 et la mantisse 0,8507 qui par lecture inverse dans la table de log donne 7091.
le produit xy est donc environ 7,091.102 = 709,1
Exemple 2 : En prenant toujours ces deux nombres, on peut tout aussi facilement calculer une valeur approchée de la racine cubique de leur quotient
La caractéristique est donc nulle, la mantisse est 0,8092 qui, par lecture inverse, donne 6445.
![\sqrt[3] \frac{x}{y}](/pictures/frwiki/51/3de5dfec01b98c8f29309862b03f3062.png) est donc environ égal à 6,445
est donc environ égal à 6,445La règle à calcul
Article détaillé : règle à calcul.Le principe de la règle à calcul est analogue à celui précédemment décrit. La précision sera seulement moindre.
Sur la règle à calcul sont placés les logarithmes des nombres de 1 à 10.
Pour effectuer le produit de xy = 436 × 1,63, on effectue, grâce à la règle à calcul le produit 4,36 × 1,63 en ajoutant les longueurs correspondant à log(4,36) et log(1,63), on obtient environ 7,1.
Le produit de xy est donc environ 7,1.102
Les échelles logarithmiques
Elles sont utilisés pour représenter des phénomènes pouvant varier de 10 − 10 à 1010. Elles permettent d'amplifier les variations des valeurs proches de 0 et de rendre moins importantes les variation pour les grands nombres, en mettant en évidence plutôt les variations relatives.
- L'utilisation des échelles logarithmiques est détaillée dans les articles échelle logarithmique, repère semi-logarithmique, repère log-log.
le pH
Article détaillé : Potentiel hydrogène.Le pH d'une solution donne le cologarithme de sa concentration en ions oxonium :
![\mathrm{pH} = -\log \big[ \mathrm H_3 \mathrm O^+ \big]](/pictures/frwiki/57/9aeebc6ba0bdbd046ef13e1561b5f489.png)
Le pH de l'eau pure est de 7, ce qui signifie qu'il y a 10 − 7 moles de H3O + dans un litre d'eau.
Le pH du jus de citron est de 2,4, ce qui signifie qu'il y a
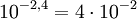 moles de H3O + dans un litre de jus de citron.
moles de H3O + dans un litre de jus de citron.On remarque qu'un pH faible correspond à une concentration élevée de H3O + donc à un milieu acide.
Les décibels
Article détaillé : Bel.En acoustique, une différence de un décibel ou un dB entre deux puissances signifie que le logarithme du rapport entre ces deux puissance est de 0,1 (un dixième de Bel). Sachant qu'un logarithme de 0,1 correspond à un nombre égal à 1,26, une augmentation de 1 dB correspond à une multiplication de la puissance par 1,26. Une multiplication de la puissance sonore par 2 correspond à une augmentation de 3 dB car 100,3 = 2 (à peu près égal).
Catégorie : Fonction remarquable
Wikimedia Foundation. 2010.

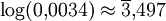
![\log \left(\sqrt[3] \frac{x}{y} \right) = \frac 13 \Big(\log(x) - \log(y) \Big) = \frac{2{,}6392 - 0{,}2115}{3} = \frac{2{,}4277}{3} = 0{,}8092](/pictures/frwiki/50/23b083e4643e45f0d07a3f80322d24fd.png)