- Repere semi-logarithmique
-
Repère semi-logarithmique
Un repère semi-logarithmique est un repère dans lequel l'un des axes, par exemple celui des abscisses (x), est gradué selon une échelle linéaire, comme les graduations d'un mètre courant, alors que l'autre axe, ici celui des ordonnées (y), est gradué selon une échelle logarithmique.
Le repère semi-logarithmique permet de représenter des phénomènes exponentiels ou, plus généralement, des mesures qui peuvent prendre des valeurs proches de 1 ou proches de 105
Exemple
Représentation graphique des termes de la suite (2n)n = 1...8 dans un repère semi-logarithmique.
x 1 2 3 4 5 6 7 8 y 2 4 8 16 32 64 128 256
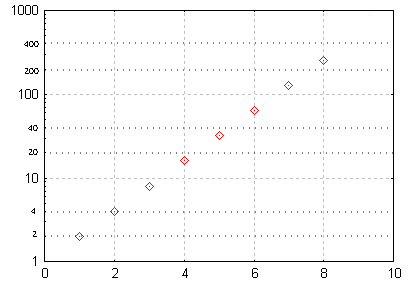
Représentation de la suite 2n dans un repère semi-logarithmiqueCe type de repère permet aussi d'évaluer les taux de croissance d'une variable évoluant avec le temps. Quel que soit le niveau de la variable, des taux de croissance identiques seront représentés par des segments ayant la même pente. On peut ainsi comparer des taux de croissance en faisant abstraction des effets d'échelle.
Voir aussi
- Portail des mathématiques
Catégorie : Système de coordonnées
Wikimedia Foundation. 2010.
