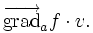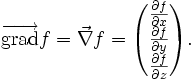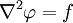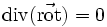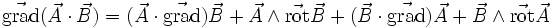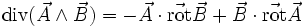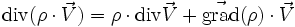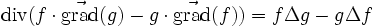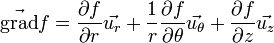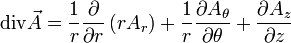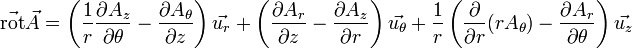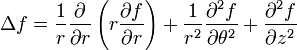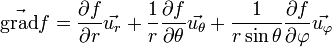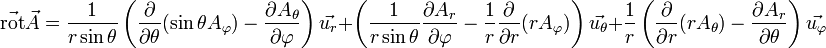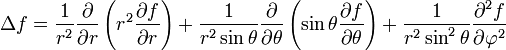- Analyse Vectorielle
-
Analyse vectorielle
Articles d'analyse vectorielle 
Objets d'étude Champ vectoriel Champ scalaire Équation aux dérivées partielles de Laplace de Poisson Opérateurs Nabla Gradient Rotationnel Divergence Laplacien scalaire Bilaplacien Laplacien vectoriel D'alembertien Théorèmes de Green de Stokes de Helmholtz de flux-divergence du gradient du rotationnel L'analyse vectorielle est une branche des mathématiques qui étudie les champs de scalaires et de vecteurs suffisamment réguliers des espaces euclidiens, c'est-à-dire les applications différentiables d'un ouvert d'un espace euclidien E à valeurs respectivement dans
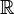 et dans E. Du point de vue du mathématicien, l'analyse vectorielle est donc une branche de la géométrie différentielle. Cette dernière inclut l'analyse tensorielle qui apporte des outils plus puissants et une analyse plus concise entre autres des champs de vecteurs.
et dans E. Du point de vue du mathématicien, l'analyse vectorielle est donc une branche de la géométrie différentielle. Cette dernière inclut l'analyse tensorielle qui apporte des outils plus puissants et une analyse plus concise entre autres des champs de vecteurs.Mais l'importance de l'analyse vectorielle provient de son utilisation intensive en physique et dans les sciences de l'ingénieur. C'est de ce point de vue que nous la présenterons, et c'est pourquoi nous nous limiterons le plus souvent au cas où
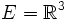 est l'espace usuel à trois dimensions. Dans ce cadre, un champ de vecteurs associe à chaque point de l'espace un vecteur (à trois composantes réelles), tandis qu'un champ de scalaires y associe un réel. Imaginons par exemple l'eau d'un lac. La donnée de sa température en chaque point forme un champ de scalaires, celle de sa vitesse en chaque point, un champ de vecteurs. (Pour une approche plus théorique, voir géométrie différentielle)
est l'espace usuel à trois dimensions. Dans ce cadre, un champ de vecteurs associe à chaque point de l'espace un vecteur (à trois composantes réelles), tandis qu'un champ de scalaires y associe un réel. Imaginons par exemple l'eau d'un lac. La donnée de sa température en chaque point forme un champ de scalaires, celle de sa vitesse en chaque point, un champ de vecteurs. (Pour une approche plus théorique, voir géométrie différentielle)Sommaire
Principaux opérateurs différentiels linéaires de tri
Le gradient, la divergence et le rotationnel sont les trois principaux opérateurs différentiels linéaires du premier ordre. Cela signifie qu'ils ne font intervenir que des dérivées partielles (ou différentielles) premières des champs, à la différence, par exemple, du laplacien qui fait intervenir des dérivées partielles du second ordre.
- On les rencontre en particulier en mécanique des fluides (équations de Navier-Stokes).
- Et aussi en électromagnétisme, où ils permettent d'exprimer les propriétés du champ électromagnétique. La formulation moderne des équations de Maxwell utilise ces opérateurs.
- Ainsi que dans toute la physique mathématique (propagation, diffusion, résistance des matériaux,...).
L'opérateur formel nabla
Article détaillé : nabla.L'opérateur nabla
 tire son nom d'une lyre antique qui avait la même forme de triangle pointant vers le bas. Il s'agit d'un opérateur formel de
tire son nom d'une lyre antique qui avait la même forme de triangle pointant vers le bas. Il s'agit d'un opérateur formel de 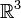 défini en coordonnées cartésiennes par
défini en coordonnées cartésiennes par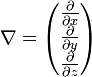 .
.
On écrit aussi
 pour souligner que formellement, l'opérateur nabla a les caractéristiques d'un vecteur. On le qualifie d'ailleurs de pseudovecteur. Il ne contient certes pas de valeurs scalaires, mais on va utiliser ses éléments constitutifs (que l'on peut voir comme des opérations en attente d'argument) très exactement comme on aurait utilisé les valeurs scalaires composant un vecteur.
pour souligner que formellement, l'opérateur nabla a les caractéristiques d'un vecteur. On le qualifie d'ailleurs de pseudovecteur. Il ne contient certes pas de valeurs scalaires, mais on va utiliser ses éléments constitutifs (que l'on peut voir comme des opérations en attente d'argument) très exactement comme on aurait utilisé les valeurs scalaires composant un vecteur.La notation nabla fournit un moyen commode pour exprimer les opérateurs vectoriels en coordonnées cartésiennes.
Le gradient
Article détaillé : gradient.Le gradient est un opérateur qui s'applique à un champ de scalaires et le transforme en champ de vecteurs. Pratiquement, le gradient indique la direction de la plus grande variation du champ scalaire, et l'intensité de cette variation. Par exemple, le gradient de l'altitude est dirigé selon la ligne de plus grande pente et sa norme augmente avec la pente.
En mathématiques, le gradient du champ f, supposé continûment différentiable, au point a, est défini par la relation
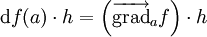 ,
,
où
 désigne la valeur sur le vecteur h de la différentielle de la fonction f au point a.
désigne la valeur sur le vecteur h de la différentielle de la fonction f au point a.C'est donc tout simplement la définition de l'application linéaire tangente du champ scalaire f(M)= f(x, y, z) en M = a . De plus, pour une surface d'équation f(x,y,z) = 0, le vecteur normal à la surface au point a = (xa,ya,za) est donné par
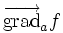 , ce qui se déduit facilement de ce qui précède.
, ce qui se déduit facilement de ce qui précède.Il en résulte immédiatement que la dérivée de la fonction en a par rapport au vecteur v est donnée par
En dimension 3 et coordonnées cartésiennes, le champ de gradients vérifie
Cette relation peut servir, dans le cas particulier où elle s'applique, de définition du gradient. Elle se généralise naturellement en dimension quelconque en ajoutant des composantes au nabla.
Application linéaire tangente d'un champ de vecteurs
Soit M' le point translaté de M par la translation de vecteur
 ; alors :
; alors :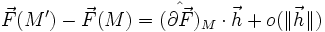
définit l'opérateur linéaire noté par un chapeau pour signifier que sa représentation dans une base est une matrice carrée [3-3], application linéaire tangente du champ de vecteurs F(M).
Le déterminant de cet opérateur est le Jacobien de la transformation qui à M associe F(M).
Sa trace définira ( voir ci-après) la divergence du champ de vecteurs F(M).
Cela permettra de donner du rotationnel du champ de vecteurs F(M) une définition intrinsèque.
On pourra vérifier que symboliquement :
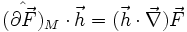
La divergence
Article détaillé : divergence (physique).La divergence s'applique à un champ de tenseurs d'ordre n et le transforme en un champ de tenseurs d'ordre n-1. Pratiquement, la divergence d'un champ de vecteurs exprime sa tendance à fluer localement hors d'un petit volume entourant le point M où est calculée la divergence.
En dimension 3 et en coordonnées cartésiennes, si
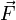 est un tenseur d'ordre 1, alors c'est un vecteur et on peut définir la divergence par la relation
est un tenseur d'ordre 1, alors c'est un vecteur et on peut définir la divergence par la relation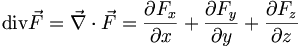
où
 désigne le champ de vecteurs auquel est appliqué l'opérateur divergence. La divergence peut être vue, formellement, comme le produit scalaire de l'opérateur nabla par le vecteur « générique » du champ auquel elle est appliquée, ce qui justifie la notation
désigne le champ de vecteurs auquel est appliqué l'opérateur divergence. La divergence peut être vue, formellement, comme le produit scalaire de l'opérateur nabla par le vecteur « générique » du champ auquel elle est appliquée, ce qui justifie la notation 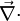 . Bien entendu, cette définition se généralise naturellement en dimension quelconque.
. Bien entendu, cette définition se généralise naturellement en dimension quelconque.La définition indépendante du choix de la base est :
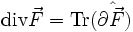
Une autre définition possible, plus générale mais plus difficile à formaliser, consiste à définir la divergence d'un champ de vecteurs en un point comme le flux local du champ autour de ce point.
Le rotationnel
Article détaillé : rotationnel.Le rotationnel transforme un champ de vecteurs en un autre champ de vecteurs. Plus difficile à se représenter aussi précisément que le gradient et la divergence, il exprime la tendance qu'a un champ à tourner autour d'un point : sa circulation locale sur un petit lacet entourant le point M est non nulle. Par exemple :
- dans une tornade, le vent tourne autour de l'œil du cyclone et le champ de vecteurs vitesse du vent a un rotationnel non nul autour de l'œil. Le rotationnel de ce champ de vitesse (autrement dit le champ de vorticité ou encore champ tourbillon) est d'autant plus intense que l'on est proche de l'oeil.
- le rotationnel du champ des vitesses
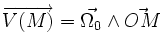 d'un solide qui tourne à vitesse constante
d'un solide qui tourne à vitesse constante 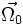 est constant, dirigé selon l'axe de rotation et orienté de telle sorte que la rotation ait lieu, par rapport à lui, dans le sens direct et vaut simplement
est constant, dirigé selon l'axe de rotation et orienté de telle sorte que la rotation ait lieu, par rapport à lui, dans le sens direct et vaut simplement 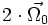
Dans un espace à 3 dimension et en coordonnées cartésiennes, on peut définir le rotationnel par la relation
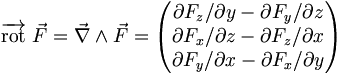
où
 désigne le champ de vecteurs auquel est appliqué l'opérateur rotationnel. L'analogie formelle avec un produit vectoriel justifie la notation
désigne le champ de vecteurs auquel est appliqué l'opérateur rotationnel. L'analogie formelle avec un produit vectoriel justifie la notation 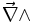 .
.Cela peut aussi s'écrire, par abus de notation, à l'aide d'un déterminant :
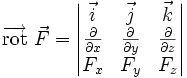
où
 désigne la base canonique. Cette dernière expression est un peu plus compliquée que la précédente, mais elle se généralise facilement à d'autres systèmes de coordonnées.
désigne la base canonique. Cette dernière expression est un peu plus compliquée que la précédente, mais elle se généralise facilement à d'autres systèmes de coordonnées.- Une définition intrinsèque (parmi d'autres) du rotationnel est la suivante :
A partir du champ
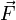 , on peut construire le champ
, on peut construire le champ 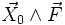 (où
(où 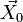 est un vecteur uniforme) dont la divergence est une forme linéaire de
est un vecteur uniforme) dont la divergence est une forme linéaire de 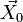 et donc exprimable par un produit scalaire
et donc exprimable par un produit scalaire 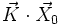 , où
, où 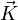 est l'opposé du rotationnel de
est l'opposé du rotationnel de 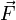 :
: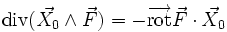
Une autre définition possible, plus générale mais plus difficile à formaliser, consiste à définir le rotationnel d'un champ de vecteurs en un point comme la circulation locale du champ autour de ce point (voir rotationnel en physique).
Opérateurs d'ordre supérieur
Le laplacien
Le plus utilisé des opérateurs d'ordre 2 est le laplacien, du nom du mathématicien Pierre-Simon Laplace. Le laplacien d'un champ est égal à la somme des dérivées secondes de ce champ par rapport à chacune des variables.
En dimension 3 et en coordonées cartésiennes, il s'écrit :
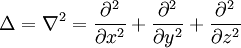 .
.
Cette définition a un sens aussi bien pour un champ de scalaires que pour un champ de vecteurs. On parle respectivement de laplacien scalaire et de laplacien vectoriel. Le laplacien scalaire d'un champ de scalaires est un champ de scalaires alors que le laplacien vectoriel d'un champ de vecteurs est un champ de vecteurs. Pour distinguer ce dernier, on le note parfois
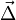 .
.L'autre notation du laplacien qui apparaît ci-dessus,
 , invite à le considérer, formellement, comme le carré scalaire de l'opérateur nabla «
, invite à le considérer, formellement, comme le carré scalaire de l'opérateur nabla «  ».
».Le laplacien apparaît dans l'écriture de plusieurs équations aux dérivées partielles qui jouent un rôle fondamental en physique.
- La plus simple est l'équation de Laplace Δf = 0. Ses solutions (de classe
 ) sont les fonctions harmoniques, dont l'étude est appelée théorie du potentiel. Ce nom provient du potentiel électrique, dont le comportement (de même que celui d'autres potentiels en physique) est régi, sous certaines conditions, par cette équation.
) sont les fonctions harmoniques, dont l'étude est appelée théorie du potentiel. Ce nom provient du potentiel électrique, dont le comportement (de même que celui d'autres potentiels en physique) est régi, sous certaines conditions, par cette équation. - Le laplacien sert aussi à écrire:
ou encore l'équation des cordes vibrantes :
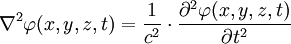
Le laplacien vectoriel
Le Laplacien d'un champ de vecteurs
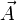 est un vecteur défini par le Laplacien scalaire de chacune des composantes du champ vectoriel, ainsi en coordonnées cartésiennes, il est défini par :
est un vecteur défini par le Laplacien scalaire de chacune des composantes du champ vectoriel, ainsi en coordonnées cartésiennes, il est défini par :
Le Laplacien vectoriel est présent :
- dans l'Équation de Poisson pour les versions vectorielles
- en mécanique des fluides visqueux où il apparait dans les Équations de Navier-Stokes
Quelques formules différentielles
Attention : les formules suivantes sont valables à condition que certaines hypothèses soient vérifiées ! (la fonction scalaire dans la première formule doit être C2(Ω), où
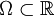 , par exemple. De même, si
, par exemple. De même, si  désigne la fonction vectorielle concernée dans la seconde formule, il faut vérifier
désigne la fonction vectorielle concernée dans la seconde formule, il faut vérifier 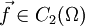 ,
,  .)
.)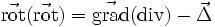 (appliqué à un vecteur) (rotationnel du rotationnel)
(appliqué à un vecteur) (rotationnel du rotationnel)
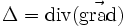 (appliqué à un scalaire)
(appliqué à un scalaire)
Formules dites de Leibniz pour les produits
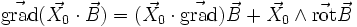 (où
(où  est un vecteur uniforme) et évidemment :
est un vecteur uniforme) et évidemment :
 (dite de Bernoulli, en mécanique des fluides)
(dite de Bernoulli, en mécanique des fluides)
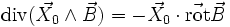 (où
(où 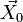 est un vecteur uniforme, définition intrinsèque du rotationnel)
est un vecteur uniforme, définition intrinsèque du rotationnel)
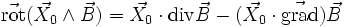 (où
(où 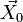 est un vecteur uniforme, par définition de l'application linéaire tangente)
est un vecteur uniforme, par définition de l'application linéaire tangente)
 (symétrique en f et g)
(symétrique en f et g)
Quelques formules utiles
- Soient f(M) et g(M) deux champs scalaires,il existe un champ de vecteurs
 tel que :
tel que :
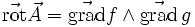
- Le champ central
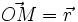 joue un rôle très important en physique. Aussi convient-il de mémoriser ces quelques évidences :
joue un rôle très important en physique. Aussi convient-il de mémoriser ces quelques évidences :
son application linéaire tangente est la matrice identité (cf. la définition !),donc
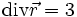 et
et 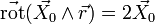 (où
(où  est un vecteur uniforme)
est un vecteur uniforme)- D'autre part
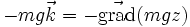 ; soit
; soit 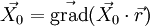 (où
(où 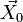 est un vecteur uniforme). Et aussi:
est un vecteur uniforme). Et aussi:
 avec
avec 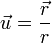
en particulier
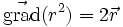 (évident car
(évident car 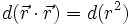 )
)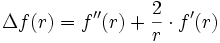 , sauf en r = 0
, sauf en r = 0
- Le champ newtonien, soit
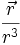 , est très souvent étudié ,
, est très souvent étudié ,
car c'est le seul champ central à divergence nulle (évident si l'on pense en termes de Flux) ( hors r = 0, où elle vaut
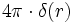 , théorème de Gauss pour l'angle solide)
, théorème de Gauss pour l'angle solide)Il en résulte que
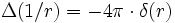
- Donc
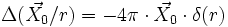
(où
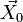 est un vecteur uniforme)
est un vecteur uniforme)qui se décompose en :
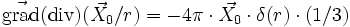 (où
(où 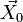 est un vecteur uniforme), et
est un vecteur uniforme), et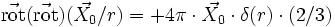 (où
(où 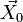 est un vecteur uniforme)
est un vecteur uniforme)ce qui est moins évident (cf. moment magnétique).
- En mécanique des fluides, il faut retenir encore quelques "évidences" supplémentaires, pour bien se familiariser avec l'analyse vectorielle avant de l'aborder.
- Les formules précédentes sont dites de calcul différentiel. Il convient de les associer aux formules de calcul intégral : formule de Stokes, théorème d'Ostrogradski, etc.
- Enfin, il convient de ne pas perdre de vue le caractère axial ou polaire des champ de vecteurs étudiés. Ce ne sont absolument pas les mêmes entités mathématiques !
Expressions des opérateurs en différentes coordonnées
Coordonnées cylindriques
Coordonnées sphériques
Voir aussi
- Théorème de Green
- Théorème de Stokes
- Identités vectorielles
- Théorème de flux-divergence
- Théorème de Helmholtz-Hodge
- Opérateurs nabla dans les coordonnées cylindriques et sphériques
- Électrostatique
- Magnétostatique
- Portail des mathématiques
- Portail de la physique
Catégories : Analyse fonctionnelle | Méthode mathématique de la physique | Analyse à plusieurs variables | Analyse vectorielle
Wikimedia Foundation. 2010.