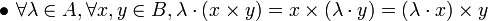Algèbre associative sur un anneau
- Algèbre associative sur un anneau
-
Algèbre associative sur un anneau
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Algèbre associative sur un anneau de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Algèbre associative sur un corps — En mathématiques, une algèbre associative sur un corps (commutatif) est un espace vectoriel dans lequel est aussi définie une multiplication des vecteurs, qui possède les propriétés de distributivité, de bilinéarité et d associativité. Autrement… … Wikipédia en Français
Algebre sur un anneau — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie … Wikipédia en Français
Algèbre Sur Un Anneau — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie … Wikipédia en Français
Algèbre sur un anneau commutatif — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie … Wikipédia en Français
Algèbre associative — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre associative (sur un anneau commutatif A) est un anneau (ou simplement un pseudo anneau) B, muni d une structure supplémentaire de module sur A et tel que la loi… … Wikipédia en Français
Algèbre sur un anneau — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre sur un anneau commutatif est une structure algébrique qui se définit comme suit: est une algèbre sur l anneau commutatif , ou une … Wikipédia en Français
Algebre associative — Algèbre associative En mathématiques, une algèbre associative est un espace vectoriel dans lequel est aussi définie une multiplication des vecteurs, qui possède les propriétés de distributivité et d associativité. Définition Une algèbre… … Wikipédia en Français
Algèbre Associative — En mathématiques, une algèbre associative est un espace vectoriel dans lequel est aussi définie une multiplication des vecteurs, qui possède les propriétés de distributivité et d associativité. Définition Une algèbre associative A sur un corps… … Wikipédia en Français
Algebre sur un corps — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie … Wikipédia en Français
Algèbre (structure) — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie … Wikipédia en Français
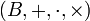 est une A-algèbre lorsque :
est une A-algèbre lorsque : est un A-module et A un anneau commutatif unitaire, l'ensemble des endomorphismes de module sur M est une A-algèbre
est un A-module et A un anneau commutatif unitaire, l'ensemble des endomorphismes de module sur M est une A-algèbre est une
est une 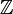 -algèbre pour la loi externe définie par
-algèbre pour la loi externe définie par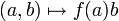 qui munit B d'une structure de A-algèbre (associative).
qui munit B d'une structure de A-algèbre (associative).
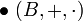 est un
est un 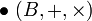 est un
est un