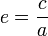- Excentricite orbitale
-
Excentricité orbitale
 Pour l’article homonyme, voir Excentricité.
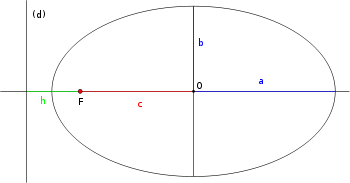
Pour l’article homonyme, voir Excentricité. L’excentricité orbitale définit la forme des orbites des objets célestes. La forme générale est une ellipse, d'équation polaire (origine au foyer) :
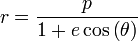 où e est l'excentricité. Elle donne ainsi une indication précise sur leur forme. Ainsi l'excentricité (e) est strictement définie pour toutes les orbites comme étant circulaire, elliptique, parabolique ou hyperbolique en prenant les valeurs suivantes :
où e est l'excentricité. Elle donne ainsi une indication précise sur leur forme. Ainsi l'excentricité (e) est strictement définie pour toutes les orbites comme étant circulaire, elliptique, parabolique ou hyperbolique en prenant les valeurs suivantes :- pour les orbites circulaires : e = 0,
- pour les orbites elliptiques : 0 < e < 1,
- pour les trajectoires paraboliques : e = 1,
- pour les trajectoires hyperboliques : e > 1.
Comme les paraboles et les hyperboles ne sont pas des courbes fermées, on ne parle plus d'orbite mais de trajectoire.
Sommaire
Calcul de l'excentricité d'une orbite
Pour les orbites elliptiques, l'excentricité d'une orbite pour être calculée en fonction de son apoapse et de son périapse :
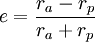 ,
,
ce qui, après simplification, donne :
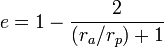 .
.
où :
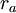 est le rayon à l'apoapse,
est le rayon à l'apoapse,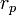 est le rayon au périapse.
est le rayon au périapse.
L'excentricité d'une orbite peut aussi se calculer de la façon suivante :
où:
 est la distance entre le centre de l'ellipse et un de ses deux foyers ; de plus ,
est la distance entre le centre de l'ellipse et un de ses deux foyers ; de plus , 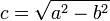
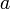 est la longueur du demi grand-axe .
est la longueur du demi grand-axe .
Excentricité des planètes du système solaire
Planète Excentricité orbitale
Époque J2000Mercure 0,205 630 69 Vénus 0,006 773 23 Terre 0,016 710 22 Mars 0,093 412 33 Jupiter 0,048 392 66 Saturne 0,054 150 60 Uranus 0,047 167 71 Neptune 0,008 585 87 Phénomènes modifiant l'excentricité
Article connexe : Cycles de Milankovitch.Lorsque deux corps sont en orbite (révolution gravitationnelle) l'un autour de l'autre, l'excentricité des orbites est théoriquement fixée au départ et ne pourrait changer. En réalité, deux phénomènes principaux peuvent la modifier. D'une part, les deux astres ne sont pas isolés dans l'espace, et l'interaction des autres planètes et corps peuvent modifier l'orbite et par là même l'excentricité. Une autre modification, interne au système considéré, est due à l'effet de marée.
Prenons l'exemple concret de la Lune tournant autour de la Terre. Comme l'orbite de la Lune n'est pas circulaire, elle est soumise à des forces de marée, qui s'exerce différemment selon le point de l'orbite où se trouve la Lune, et varient continuement au cours de la révolution de la Lune. Les matériaux à l'intérieur de la Lune subissent donc des forces de friction, qui sont dissipatrices d'énergie, et qui tendent à rendre l'orbite circulaire, pour minimiser cette friction. En effet, l'orbite circulaire synchrone (la Lune montrant toujours la même face à la Terre) est l'orbite minimisant les variations des forces de marée.→ Lorsque deux astres sont en rotation l'un autour de l'autre, l'excentricité des orbites a donc tendance à diminuer.
Dans un système type « planète/satellite » (corps de faible masse en rotation autour d'un corps de masse élevée), le temps nécessaire pour atteindre l'orbite circulaire (temps de circularisation) est beaucoup plus élevé que le temps nécessaire pour que le satellite présente toujours la même face à la planète (temps de « synchronisation »). La Lune présente ainsi toujours la même face à la Terre, sans que son orbite soit circulaire.
L'excentricité de l'orbite terrestre est elle-aussi variable sur de très longues périodes (en centaines de millions d'années), essentiellement par intéraction avec les autres planètes. La valeur actuelle est d'environ 0,0167, mais dans le passé elle a déjà atteint une valeur maximale de 0,07 [1].
Impact sur le climat
La mécanique orbitale exige que la durée des saisons soit proportionnelle à la superficie de l'orbite de la Terre qui a été balayée entre les solstices et les équinoxes. Par conséquent, quand l'excentricité orbitale est proche des maximums, les saisons qui se produisent à l'aphélie sont sensiblement plus longues.
À notre époque, la Terre arrive à son périhélie en début janvier, dans l'hémisphère nord, l'automne et l'hiver se produisent lorsque la Terre est aux zones où sa vitesse de parcours de son orbite est la plus élevée. Par conséquent, l'hiver et l'automne (septentrionaux) sont légèrement plus courts que le printemps et l'été. En 2006, l'été a été 4,66 jours plus long que l'hiver et le printemps 2,9 jours plus long que l'automne[2]. C'est évidemment l'inverse pour la durée des saisons australes !Par l'action combinée entre la variation d'orientation du grand axe de l'orbite terrestre[3] et de la précession des équinoxes, les dates d'occurence du périhélie et de l'aphélie avancent lentement dans les saisons[4].
Dans les 10 000 prochaines années, les hivers de l'hémisphère nord deviendront progressivement plus longs et les étés plus courts. Toute vague de froid sera néanmoins compensée par le fait que l'excentricité de l'orbite terrestre sera presque réduite de moitié[réf. souhaitée], réduisant le rayon moyen de l'orbite, augmentant ainsi les températures dans les deux hémisphères[réf. nécessaire].Notes et Références
- ↑ Asteroids
- ↑ Ice Ages, Sea Level, Global Warming, Climate, and Geology
- ↑ Par rapport à un référentiel lointain.
- ↑ Ce qui se traduit par l'augmentation de l'argument du périhélie.
Voir aussi
- Portail de l’astronomie
Catégorie : Orbite
Wikimedia Foundation. 2010.