- Absolue Continuité
-
Absolue continuité
En mathématiques, on introduit les notions de fonction absolument continue et de mesure absolument continue. Ces deux concepts entretiennent des rapports.
Sommaire
Fonction absolument continue
Motivation
Une fonction continue
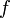 sur un intervalle est égale à la dérivée de son intégrale
sur un intervalle est égale à la dérivée de son intégrale 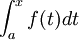 (théorème fondamental de l'analyse). Dans un cadre plus général, celui de l'intégrale de Lebesgue, une fonction
(théorème fondamental de l'analyse). Dans un cadre plus général, celui de l'intégrale de Lebesgue, une fonction 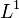 est égale presque partout à la dérivée de son intégrale. Par contre, une fonction presque partout dérivable, même si la dérivée est
est égale presque partout à la dérivée de son intégrale. Par contre, une fonction presque partout dérivable, même si la dérivée est 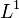 , peut ne pas être égale à l'intégrale de sa dérivée. L'escalier du diable, ou escalier de Cantor, est un exemple de ce phénomène. Travailler dans l'espace des fonctions absolument continues assure que les fonctions considérées sont bien égales à l'intégrale de leur dérivée.
, peut ne pas être égale à l'intégrale de sa dérivée. L'escalier du diable, ou escalier de Cantor, est un exemple de ce phénomène. Travailler dans l'espace des fonctions absolument continues assure que les fonctions considérées sont bien égales à l'intégrale de leur dérivée.Définition
Soit
![\scriptstyle\ A=[a,b]\,](/pictures/frwiki/55/7dd8bc285d7632af5c3820f31f9a4a5d.png) un intervalle. On dit que la fonction
un intervalle. On dit que la fonction 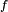 est absolument continue sur
est absolument continue sur 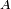 si, pour tout réel
si, pour tout réel 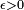 , il existe un
, il existe un 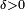 tel que, pour toute suite
tel que, pour toute suite ![\scriptstyle\ ([a_n, b_n])_{n \in \mathbb{N}} \,](/pictures/frwiki/57/9cd71463cf52d8cd312db1c163a13e48.png) de sous-intervalles de
de sous-intervalles de 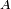 d'intérieurs disjoints,
d'intérieurs disjoints,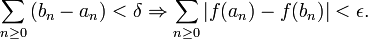
Propriétés
- Si une fonction
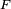 est continue sur un segment
est continue sur un segment ![\scriptstyle\ [a,b]\,](/pictures/frwiki/52/4becf89d9431b5fef61d8eccb10ce6f0.png) , alors il existe une fonction
, alors il existe une fonction 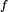 intégrable sur
intégrable sur ![\scriptstyle\ [a,b]\,](/pictures/frwiki/52/4becf89d9431b5fef61d8eccb10ce6f0.png) (au sens de Lebesgue) telle que pour tout
(au sens de Lebesgue) telle que pour tout ![\scriptstyle\ x \in [a,b],](/pictures/frwiki/98/b6eadf260703b191c17dc8a0313361a5.png)
si et seulement si
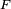 est absolument continue sur
est absolument continue sur ![\scriptstyle\ [a,b].](/pictures/frwiki/53/51b8152cc3f0b2ae7d1f99468dd26c42.png)
- Toute fonction absolument continue sur un intervalle est à variation bornée sur cet intervalle.
- Si
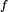 est absolument continue sur l'intervalle
est absolument continue sur l'intervalle ![\scriptstyle\ [a,b],](/pictures/frwiki/50/28291e3030afeb6928d7105b9dc13bbe.png) alors elle possède la propriété N de Luzin : l'image par
alors elle possède la propriété N de Luzin : l'image par 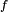 de tout ensemble de mesure nulle (pour la mesure de Lebesgue) est de mesure nulle.
de tout ensemble de mesure nulle (pour la mesure de Lebesgue) est de mesure nulle. - Si
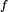 est absolument continue, alors
est absolument continue, alors 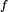 est dérivable presque partout.
est dérivable presque partout. - Si
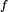 est continue, à variation bornée et possède la propriété N de Luzin, alors elle est absolument continue.
est continue, à variation bornée et possède la propriété N de Luzin, alors elle est absolument continue.
Contre-exemple
La fonction continue qui a pour graphe l'escalier du diable n'est pas absolument continue : l'image de l'ensemble de Cantor, qui est de mesure nulle, est
![\scriptstyle\ [0,1]\,](/pictures/frwiki/57/9d57564f8f7076f7007ec675fbb6ec00.png) tout entier.
tout entier.Mesure absolument continue
Soient
 et
et  deux mesures complexes sur un espace mesuré
deux mesures complexes sur un espace mesuré 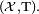 On dit que
On dit que  est absolument continue par rapport à
est absolument continue par rapport à  si et seulement si pour tout ensemble mesurable
si et seulement si pour tout ensemble mesurable 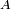 ,
,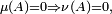 ce que l'on note
ce que l'on note 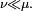
Le théorème de Radon-Nikodym donne une autre caractérisation dans le cas où
 est positive,
est positive,  finie et
finie et  est complexe,
est complexe, 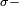 finie: il existe alors
finie: il existe alors 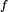 fonction mesurable telle que
fonction mesurable telle que 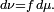 La fonction
La fonction 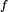 est appelée densité de la mesure
est appelée densité de la mesure  par rapport à la mesure
par rapport à la mesure 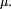
Lien entre fonction réelle absolument continue et mesure absolument continue
Une fonction
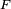 est localement absolument continue si et seulement si sa distribution dérivée est une mesure absolument continue par rapport à la mesure de Lebesgue. Par exemple, une mesure
est localement absolument continue si et seulement si sa distribution dérivée est une mesure absolument continue par rapport à la mesure de Lebesgue. Par exemple, une mesure  bornée sur l'ensemble des boréliens de la droite réelle est absolument continue par rapport à la mesure de Lebesgue si et seulement si la fonction de répartition associée
bornée sur l'ensemble des boréliens de la droite réelle est absolument continue par rapport à la mesure de Lebesgue si et seulement si la fonction de répartition associéeest localement une fonction absolument continue.
Voir aussi
- Théorème de Radon-Nikodym
- Fonction à variation bornée
- Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]
- Portail des mathématiques
Catégories : Analyse | Analyse réelle | Théorie de la mesure - Si une fonction
Wikimedia Foundation. 2010.

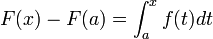
![F:x\mapsto\mu(]-\infty,x])](/pictures/frwiki/57/9e8a37379ea8ed681dd59729d2dc7079.png)