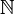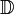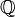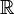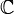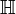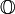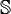- Nombres entiers
-
Entier relatif
 Pour les articles homonymes, voir Entier (homonymie).
Pour les articles homonymes, voir Entier (homonymie).En mathématiques, un entier relatif (ou entier rationnel) est un nombre entier (c'est-à-dire sans partie fractionnaire) et muni d'un signe positif ( + ) ou négatif ( − ). L'ensemble
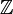 des entiers relatifs est composé des entiers naturels 0, 1, 2, ... dits entiers relatifs positifs et de leurs opposés 0, -1, -2, -3, ... appelés entiers relatifs négatifs.
des entiers relatifs est composé des entiers naturels 0, 1, 2, ... dits entiers relatifs positifs et de leurs opposés 0, -1, -2, -3, ... appelés entiers relatifs négatifs.La principale raison de l'introduction des nombres négatifs est la possibilité de résoudre toutes les équations de la forme :
- a + x = b, où x est l'inconnue et a et b sont des paramètres.
Dans l'ensemble des entiers naturels, seules certaines de ces équations ont une solution.
- 5 + x = 8 si et seulement si x = 3
- 9 + x = 4 n'a pas de solution dans l'ensemble des entiers naturels. Elle possède une solution dans l'ensemble des entiers relatifs qui est -5.
Sommaire
Fragments d'histoire
La première allusion à des nombres négatifs apparaît dans des textes indiens comme l'Arybhatiya du mathématicien indien Âryabhata (476 - 550) où sont définies les règles d'additions et de soustractions. Les nombres négatifs apparaissent alors comme représentant des dettes et les nombres positifs comme des recettes. Quelques siècles plus tard, dans les écrits du mathématicien perse Abu l-Wafa (940 - 998), on voit apparaïtre des produits de nombres négatifs par des nombres positifs. Cependant le nombre reste encore attaché à des quantités physiques et le nombre négatif n'a guère de statut légal. al Khuwarizmi (783 - 850) par exemple, dans son ouvrage la Transposition et la réduction préfère traiter 6 types d'équations du second degré au lieu d'envisager des soustractions.
En Europe les nombres relatifs apparaissent tardivement, on attribue en général à Simon Stevin (1548 - 1620) la fameuse règle des signes pour le produit de deux entiers relatifs. D'Alembert (1717 - 1783) lui-même dans l'encyclopédie envisage le nombre relatif comme une idée dangereuse.
« Il faut avouer qu'il n'est pas facile de fixer l'idée des quantités négatives, & que quelques habiles gens ont même contribué à l'embrouiller par les notions peu exactes qu'ils en ont données. Dire que la quantité négative est au-dessous du rien, c'est avancer une chose qui ne se peut pas concevoir. Ceux qui prétendent que 1 n'est pas comparable à - 1[1] , & que le rapport entre 1 & -1 est différent du rapport entre - -1 & 1, sont dans une double erreur: 1(...) Il n'y a donc point réellement & absolument de quantité négative isolée: - 3 pris abstraitement ne présente à l'esprit aucune idée. » (D'Alembert, dictionnaire raisonné des sciences, des arts et des métiers)
Il faut attendre encore deux siècles et l'avènement du formalisme pour voir apparaître une construction formelle de l'ensemble des entiers relatifs à partir de classes d'équivalence de couples d'entiers naturels
- Article détaillé : construction des entiers relatifs
C'est à Richard Dedekind (1831 - 1916) que l'on doit cette construction. Lui-même utilisait la lettre K pour désigner l'ensemble des entiers relatifs. Plusieurs autres conventions ont eu cours, jusqu'à ce que Nicolas Bourbaki popularise l'usage de la lettre
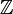 , initiale de l'allemand Zahlen (nombre)[2]
, initiale de l'allemand Zahlen (nombre)[2]Règles opératoires
Dans un nombre relatif, on distingue son signe (+ ou - ) et sa valeur absolue : - 3 a pour valeur absolue 3.
Addition
La somme de deux entiers de même signe s'obtient en additionnant les deux valeurs absolues et en conservant le signe commun
- (-3) + (-5) = -8 écriture que l'on abrège en -3 - 5 = - 8 supprimant le signe opératoire +
La somme de deux entiers relatifs de signe contraire s'obtient en calculant la différence entre les deux valeurs absolue et en lui affectant le signe de l'entier ayant la plus grande valeur absolue
- (+3) + (-5) = - 2 écriture que l'on abrège en 3 - 5 = - 2
Multiplication
Le résultat d'une multiplication s'appelle un produit. Le produit de deux nombres relatifs de même signe est toujours positif (+) et s'obtient en effectuant le produit des valeurs absolues:
- (+3) × (+4) = +12 que l'on abrège en 3 × 4 = 12
- (-3) × (-7)= + 21 = 21
(le + n'étant pas obligatoire si le produit n'est pas négatif)
Le produit de deux nombres relatifs de signes différents est toujours négatif (-) et s'obtient en effectuant le produit des valeurs absolues
- (+7) × (- 4) = - 28
Règle des signes
- plus multiplié par plus, donne produit plus.
- moins multiplié par moins, donne produit plus
- moins multiplié par plus ou plus multiplié par moins donne produit moins
Structure
L'ensemble
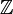 , muni de ses deux lois: + et ×, forme un des premiers exemples d'anneau commutatif unitaire :
, muni de ses deux lois: + et ×, forme un des premiers exemples d'anneau commutatif unitaire :- (
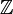 , +) est un groupe commutatif (la loi + est associative, commutative, possède un élément neutre 0, chaque élément possède un symétrique, c'est d'ailleurs pour obtenir cette propriété que furent introduits les nombres négatifs)
, +) est un groupe commutatif (la loi + est associative, commutative, possède un élément neutre 0, chaque élément possède un symétrique, c'est d'ailleurs pour obtenir cette propriété que furent introduits les nombres négatifs) - (
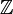 , ×) est un monoïde (la loi est associative, commutative, possède un élément neutre 1)
, ×) est un monoïde (la loi est associative, commutative, possède un élément neutre 1) - la loi × est distributive pour la loi +
Les entiers relatifs forment un ensemble dénombrable infini.
La branche des mathématiques qui traite des nombres entiers est la théorie des nombres.
Notes
- ↑ paradoxe classique : si -1 < 1 alors les inverses de ces deux nombres seraient rangés dans l'ordre inverse : l'inverse de -1 est -1 et l'inverse de 1 est 1 donc -1 > 1. paradoxe qui provient de la phrase incomplète "les inverses de ces deux nombres seraient rangés dans l'ordre inverse ", il faudrait préciser "les inverses de deux nombres de même signe sont rangés dans l'ordre inverse". Voir l'article fonction inverse pour plus d'informations.
- ↑ (en) Earliest Uses of Symbols of Number Theory
Voir aussi
- Portail des mathématiques
Catégorie : Type de nombre
Wikimedia Foundation. 2010.