- Dimension Combinatoire
-
Dimension combinatoire
Sans rentrer dans les détails, bien que cette notion de dimension redonne la dimension intuitive d'un espace (1 pour une courbe, 2 pour une surface, etc.), elle ne s'applique en réalité (c'est-à-dire avec pertinence) qu'à certains espaces topologiques un peu tordus (par rapport à la tradition des espaces métriques) : par exemple, les schémas ou les variétés algébriques, munis de la topologie de Zariski. Dans ces espaces, la nature de la topologie est plus combinatoire que géométrique.
Définition
Soit donc X un espace topologique. La dimension topologique de X est la longueur n maximale d'une suite strictement croissante de fermés irréductibles non-vides
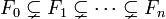 .
.Intuition - exemple
Considérons une surface (algébrique) S, par exemple une paraboloïde. On la munit de la topologie de Zariski, c'est-à-dire qu'on s'intéresse à une classe particulière de sous-objets (de sous-ensembles) de S, qu'on appelle des fermés irréductibles Zariski de S et qui sont :
- d'abord, les fermés triviaux que sont S elle-même et l'ensemble vide ;
- les coubres dessinées sur S (on ne rentre pas dans les détails ; on se contente d'une intuition) ;
- les points de S.
Les fermés de S sont les unions finies de fermés irréductibles.
Alors, la surface est de dimension topologique 2. En effet, si on cherche la plus longue suite strictement croissante de fermés irréductibles de S, on part d'un point, qu'on inclut dans une courbe dessinées sur S (il y a plein de choix possibles), qu'on inclut dans S.
Commentaire
Le concept de dimension topologique pour un espace topologique général ne s'applique utilement qu'aux espaces munis de la topologie de Zariski. On se rend compte ainsi que la topologie de Zariski, en quelque sorte, détourne le concept de topologie de sa fonction initiale de décrire l'espace usuel, et l'utilise dans une orientation beaucoup plus combinatoire.
- Portail des mathématiques
Catégorie : Topologie
Wikimedia Foundation. 2010.
