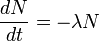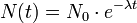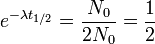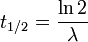- DT50
-
Demi-vie
La demi-vie est le temps mis par une substance (médicament, noyau radioactif, ou autres) pour perdre la moitié de son activité pharmacologique, physiologique ou radioactive. En particulier, dans le domaine de la radioactivité, le temps de demi-vie correspond au moment où la moitié des noyaux radioactifs d'une source se sont désintégrés.
Sommaire
En biologie et pharmacologie
En pharmacologie, la demi-vie désigne par extension le temps nécessaire pour que la quantité d’une substance contenue dans un système biologique soit diminuée de la moitié de sa valeur initiale (par exemple la teneur d’un médicament dans le plasma sanguin).
Ce paramètre varie légèrement d'un individu à l'autre, selon le processus d'élimination et le fonctionnement relatif chez l'individu.
En pratique, on considère qu'un médicament n'a plus d'effet pharmacologique après cinq à sept demi-vies.
En biologie, la demi-vie d'une enzyme correspond au temps nécessaire pour que l'enzyme perde la moitié de son activité spécifique pour cause de dénaturation et d'inactivation.
En physique nucléaire
En physique nucléaire, la demi-vie, appelée parfois période radioactive, pour un isotope radioactif, est la durée au cours de laquelle son activité radioactive décroît de moitié pour un mode de désintégration donné. Le terme demi-vie ne signifie pas que l’activité d'un isotope radioactif est nulle au bout d'un temps égal à 2 demi-vies, puisque l'activité est alors réduite seulement à 25% de l’activité initiale (voir le tableau de décroissance de l'activité). En réalité, l'activité A vaut, après n demi-vies,
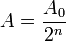 , si bien que l'activité n'est jamais mathématiquement nulle.
, si bien que l'activité n'est jamais mathématiquement nulle.C'est une propriété statistique : durée à l'issue de laquelle le noyau d'un atome radioactif aurait une chance sur deux de se désintégrer suivant le mode de désintégration concerné si ce mode était seul. Cette propriété à l'échelle du noyau atomique ne dépend pas des conditions d'environnement, telles que température, pression, champs, mais uniquement de l'isotope et du mode de désintégration considérés.
La demi-vie peut varier considérablement d'un isotope à l'autre, depuis une fraction de seconde à des millions ou des milliards d'années (voir figure ci-contre).
L'activité d'un nombre donné d'atomes d'un isotope radioactif est proportionnelle à ce nombre et inversement proportionnelle à la demi-vie de l'isotope.
Loi de décroissance radioactive
Nombre de
demi-vie
passéesFraction
restantePourcentage
restant0 1 100% 1 1/2 50% 2 1/4 25% 3 1/8 12,5% 4 1/16 6,25% 5 1/32 3,125% 6 1/64 1,5625% 7 1/128 0,78125% ... ... N 1 / 2N 100 / 2N % La décroissance radioactive est un processus de Poisson. La probabilité de désintégration est indépendante du passé et du futur. Pour la dérivation de la loi de probabilité il faut introduire une échelle de temps proportionnelle à la demi-vie. Pour cela on introduit la probabilité cumulative.
- U(t)=Prob{T>t}
La probabilité d'une désintégration après un temps t. Puisque la désintégration est indépendante de l'instant t, U(t) est la probabilité conditionnelle qu'il y ait une désintégration à l'instant t+s sachant qu'il n'y a pas de désintégration à l'instant t U(t+s)/(U(s)). Ainsi la probabilité cumulative satisfait cette équation :
- U(t+s)=U(t)U(s)
Dans le cas d'une fonction mesurable l'unique solution est la fonction exponentielle. Soit un ensemble constitué de N éléments dont le nombre décroît avec le temps selon un taux de décroissance noté λ. L'équation de ce système dynamique (cf. loi de décroissance exponentielle) s'écrit :
où λ est un nombre positif, avec une quantité initiale N(t = 0) = N0.
Si on effectue une résolution des équations différentielles à coefficients constants, alors la solution d'une telle équation est la fonction définie par :
Cette fonction décroissante atteint une valeur égale à la moitié de la quantité initiale N0 au bout d'une certaine durée notée t1 / 2. En simplifiant, on obtient alors :
d'où l'on déduit facilement
Cette durée t1 / 2 est appelé la demi-vie des éléments de l'ensemble.
Remarques
Dans les radionucléides où des particules se transforment par radioactivité en une autre particule, le nombre de particules initiales décroît exponentiellement en fonction du temps.
Il est fréquent qu'un isotope radioactif comporte plusieurs modes de désintégration, ou bien qu'il appartienne à une chaîne de désintégration radioactive. Pour ces cas, la loi exponentielle simple de décroissance radioactive ne s'applique plus, et la décroissance de l'activité de la substance est alors encore plus lente.
Voir aussi
- Période radioactive, Décroissance radioactive
- Décroissance exponentielle
- Distribution exponentielle
- Temps de doublement
- Portail de la physique
- Portail de la chimie
Catégories : Biochimie | Chimie générale | Réaction chimique | Radiochimie | Physique nucléaire | Pesticide
Wikimedia Foundation. 2010.